by David Stapleton, Ph.D., Gina Livermore, Ph.D. and Adam Tucker of The Lewin Group, Inc., for the Office of the Assistant Secretary for Planning and Evaluation, Department of Health & Human Services, July 25, 1997. Kelleen Kaye and Gilbert Crouse were the Project Officers.
This study has greatly benefitted from the assistance and comments provided by many people. Foremost among these are the Project Officers for the Office of the Assistance Secretary for Planning and Evaluation (ASPE), Kelleen Kaye, and Gilbert Crouse. Other government staff who contributed substantially to this effort are former Deputy Assistant Secretary for Human Services Policy, Wendell Primus, Leonard Sternbach (Administration for Children and Families), and Donald Oellerich (ASPE).
We are also are especially grateful to Professor Robert Moffitt (the Johns Hopkins University), who reviewed our analysis plan and provided several helpful suggestions, and for the reviews of preliminary findings provided by five experts on the history of AFDC caseloads in the states we selected for case study: Dr. Thomas Corbett, the Associate Director of the Institute for Research on Poverty at the University of Wisconsin-Madison; Werner Schink, Chief of the Research Branch of the California Department of Social Services; Dr. Steven Thompson of the Regional Economic Studies Institute of Towson State University, Maryland; Donald Winstead, the Welfare Reform Administrator for Florida's Economic Services Program; and Professor Michael Wiseman of The Robert M. La Follette Institute of Public Affairs at the University of Wisconsin-Madison.
We also received many helpful comments on our preliminary findings from participants at the RAND conference on "New Advances in Welfare Research," (Santa Monica, CA, September 10-21, 1996). Finally, we greatly appreciate the assistance provided by many anonymous individuals in collecting the data and other information that were instrumental to the success of this project.
"Chapter One: Introduction and Summary
A. BACKGROUND AND PURPOSES
In recent years many states have made substantial changes to their Aid to Families with Dependent Children (AFDC) programs on Federal 1115 Waivers, and the recent enactment of the Personal Responsibility and Working Opportunity Reconciliation Act of 1996 ensures that many more, large changes will be implemented in the not too distant future. The anticipated growth in state-level experimentation makes it especially important to improve our understanding of state-level factors behind historical growth in AFDC caseloads, for several reasons.
First, a better understanding of the impact of changes in the state economy will help states better prepare for the fiscal implications of economic recessions and recoveries under block grants.
Second, a better understanding of state-level factors behind program growth will help states design, and understand the implications of, program changes. This analysis cannot provide significant insight on the impacts of reforms such at time limits, work requirements or various restrictions on benefits because there has been little historical experience relevant to these reforms. However, the analysis can provide valuable insights on the effects of changes in basic program parameters for cash assistance, and how changes in programs such as Medicaid, SSI and Food Stamps interact with AFDC. We have more historical experience with these changes and while some research has already been done in this area, the results have been mixed or inconclusive. This analysis will help determine how realistic it is to expect proposed program changes to substantially reduce welfare dependency without impoverishing children.
Third, a better understanding of state-level factors behind historical growth will also improve our ability to establish baseline levels of program participation in a state for comparison to actual levels of participation under a state reform. As states implement reforms under the new welfare law, it will be very important to separate the impacts of those reforms on caseloads from the effects of environmental factors. Currently, caseloads are declining in most states. Are these due to legislated and administrated reforms, improvement in the economy, or some combination?
For these reasons, the Office of the Assistant Secretary for Planning and Evaluation (ASPE) in the U.S. Department of Health and Human Services has a strong interest in promoting research aimed at better understanding the determinants of AFDC participation at the state level. As part of their effort in this area, ASPE has contracted with The Lewin Group, Inc. to analyze the relationship between state AFDC caseload growth and (1) the strength and structure of the state economy; (2) demographic trends; and (3) changes in the structure of AFDC and other public assistance programs using state-level data to estimate pooled time-series models of program participation. This is the project's final report.
It is important to keep in mind that the purpose of this effort was not to build a better forecasting model. Many efforts to model AFDC participation, especially using time-series data at the national or state level, are motivated by the need to project future caseloads and expenditures. Such efforts place a priority on building a model that fits the historical series well, using whatever predictors are available. They do not necessarily require a more fundamental understanding of the relationship between the predictors and the historical series. In contrast, we place greater emphasis on developing and assessing explanatory variables that derive from theoretical considerations on the overall fit of the model.
While our findings on AFDC participation are of interest in their own right, they also serve to illustrate the potential of the methodology we use, as well as its weaknesses. We have previously applied the methodology to studies of participation in SSA's disability programs, Social Security Disability Insurance (SSDI) and Supplemental Security Income (SSI), and obtained much stronger findings about the effects of labor markets and general assistance programs on program participation than had been found in earlier studies. The methodology could also be applied to state-level indicators of the well-being of children or other vulnerable groups. Tobin (1994) has, for instance, applied the methodology to understanding determinants of the poverty rate with some success.(1) Gaylin and McLanahan (1995) have applied the methodology to studying determinants of out-of-wedlock births. The approach we take views state-level events as "natural experiments" that allow the examination of their impacts on key outcome variables. For the AFDC program, the level of experimentation has increased markedly in recent years and is likely to mushroom in the next few years. Interest in this methodology is likely to grow as a result.
Our work builds on the strengths of several previous studies that have used the same general approach (see Chapter 2). With the assistance of staff at ASPE and the Administration for Children and Families (ACF), we undertook an ambitious effort to develop a quarterly, state-level data set for the 1979-94 period. This effort has been rewarded with some results that are substantially stronger than previous results, especially concerning the impact of business cycles and of changes in basic program parameters (maximum monthly benefits, the average tax and benefit reduction rate, and the gross income limit). In other ways, however, we have not made as much progress in understanding the determinants of caseload growth as we would have liked. While we better understand the substantial caseload fluctuations during the period studied, an underlying trend remains unexplained, and we have very limited new findings concerning the effects of other state programs and policies on AFDC participation. Nonetheless, our findings clearly demonstrate the promise of this approach, and they could no doubt be strengthened through: expansion of the database to the post-1994 period and to earlier years; further development of some explanatory variables; and further experimentation with the model's specification and methods of estimation.
We estimate separate participation models for the Basic and Unemployed Parent (UP) programs. We focus on caseload models for each program, but also estimate total recipient and child recipient models. In addition, we estimate an average monthly benefit model for the combined programs.
Because the focus of this study is participation at the state level, we have also used our "best" estimated model to analyze the history of program participation in four selected states over the sample period: California, Florida, Maryland, and Wisconsin. We chose these states in part because their caseload histories have been carefully analyzed by others. California and Florida are both large states with rates of caseload growth during the latter part of our sample period that are well above the national rate. Maryland's caseload declined substantially relative to the national caseload during the middle part of the period. Wisconsin's caseload was essentially stable in the last few years of the sample, when caseloads in most other states were growing substantially. This exercise serves two purposes: determining how well the model, built on the varied experiences of all states, fits individual state caseload series, and improving our understanding about the causes of caseload growth in these states.
B. NATIONAL CASELOAD TRENDS
Caseload growth rates have varied substantially since 1980. Exhibit 1.1 shows changes in AFDC caseload growth from 1980 through 1994, which is the period for this analysis. While absolute changes in participation have been much greater for the Basic program than for the much smaller Unemployed Parent (UP) program, relative changes have been greater for the latter. In order to illustrate this, we have plotted the national participation series for the two programs on the logarithmic scale; on this scale, the slope of a series at any point is equal to its rate of growth. Official periods of economic recession are also shown for reference purposes.
After peaking in 1981 at 3.6 million, the AFDC Basic caseload fell and then rose slowly until 1989, growing from 3.3 million to 3.5 million. Between 1989 and 1994, the Basic caseload rose by more than 40 percent, from 3.6 to 5.1 million. Recent data, not shown in Exhibit 1.1, show that the caseload has once again begun to decline, from 5.1 million in March 1994 to 4.1 million in January 1997.
Like the Basic program, the UP caseload grew rapidly from 1980 to 1981, but then, unlike the Basic caseload, it continued to rise through 1984. The average annual growth rate during this period was about 25 percent. The UP caseload peaked in 1984 at just over 300,000 and then fell gradually through 1990 -- again departing from the pattern observed for the Basic caseload. The Family Support Act of 1988 required all states operating AFDC programs to also have an UP program by 1990. Since 1990, the UP caseload has risen steadily, surpassing its previous peak in 1984, although it would not have reached that peak if only states with UP programs in place before 1990 were counted.
Based on the national time series, it would appear that the UP caseload is more sensitive to economic recessions than the Basic caseload--not surprising given the nature of the program. Another evident feature of the UP caseload series is its seasonal behavior, with higher caseloads in the winter and spring than in the summer and fall.
Exhibit 1.1
AFDC Basic and UP Caseloads, 1980-1994
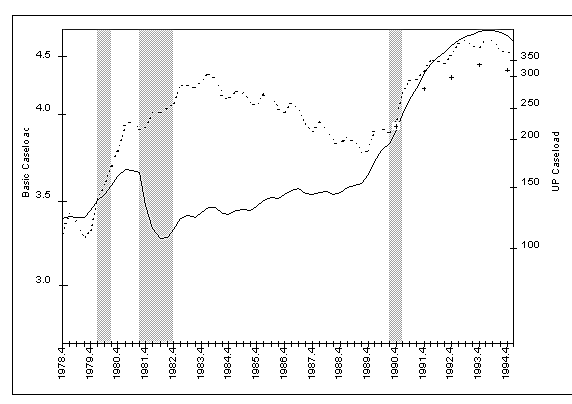
Note: Basic caseloads (solid line) are in millions of cases and UP caseloads (broken line) are in thousands of cases. Both Basic and UP cases are graphed in logarithmic scale. The plus signs trace the growth of UP programs after October 1990 excluding caseloads from states that initiated UP programs in accordance with the Family Support Act of 1988. Vertical lines show official recession periods.
Source: Office of Family Assistance (various years) and CBO (1993).
C. CONCEPTUAL FRAMEWORK
1. The Participation Decision and Other Choices
We approach this project from an economic perspective. This perspective emphasizes the role of individuals making choices between various alternatives as key to understanding individual behaviors such as labor force participation, marriage, fertility, and participation in AFDC. It posits that there are many adults for whom modest changes in factors affecting the economic attractiveness of various alternatives will influence their behaviors in these areas, although it also recognizes that the behaviors of many others may be immune from even very large changes in these same factors.
It is important to recognize that an unmarried parent's (usually a mother's) decision to seek AFDC Basic benefits is not necessarily a decision that is made taking other critical aspects of her life as given. Instead, that decision may just be one dimension of a set of "life decisions" concerning fertility, marriage, employment, and many other things. Hence, showing that AFDC Basic participation is positively related to the number of female-headed households containing children under the age of 18 -- as many studies have done--begs the question of what determines the number of such households. To some extent the number of such households and AFDC participation are jointly determined by the same factors.
Because the decision to apply for benefits may be made in conjunction with other life decisions, any factor that influences the relative well-being of the (potential) parents under all of their various "life alternatives" is a potential determinant of AFDC participation. The most obvious economic factor is the strength of the economy. A decline in job opportunities will make AFDC participation relatively more attractive than work to an unmarried mother. It may also, for instance, make family formation less attractive because of reduced job opportunities for both herself and her potential partner.
Declines in job opportunities can also have an impact on fertility, although the direction of the effect depends on the relative strength of competing forces. On the one hand, if one has a child she will need to use a share of her reduced income to provide for the child. On the other hand the "opportunity cost" of time she devotes to having and raising a child is reduced; i.e., when her potential wage rate is lowered, she gives up less when she uses her time to raise children rather than work. An additional incentive in favor of having a child exists if the woman does not have children already: it gives her access to AFDC benefits, which may substantially offset the income losses due to her poorer job prospects. (2)
Changes in programmatic factors, such as the level of benefits and eligibility criteria, also lead to changes in AFDC caseloads. Provisions of the Omnibus Budget Reconciliation Act of 1981 clearly reduced caseload growth. In more recent years, several important changes brought about by Federal legislation may also have had an effect on the AFDC caseload. The 1988 Family Support Act (FSA) created the Job Opportunities and Basic Skills (JOBS) program and mandated that all states operate a UP program. In addition, many states have received Federal waivers that allow them to experiment with various policies, often with the intended effect of moving people from welfare to work or reducing dependence on AFDC in other ways.
As with changes in job opportunities, the influence of changes in programmatic factors on participation may partly work through their impact on marital, fertility, and other decisions. For instance, introduction of the UP program was expected to reduce the number of unmarried mothers because it increased the availability of AFDC benefits to households with two parents. In theory, however, making AFDC benefits more available to two-parent families makes childbearing more attractive.
While there is much disagreement in the literature about the influence of economic factors on various life decisions, there is little doubt that these decisions are influenced by a common set of factors and, to some extent, are jointly made. Hence, it is critical to recognize the potentially joint nature of these decisions in research on AFDC participation.
Changes in other programs that provide benefits to the low-income population can also have an impact on AFDC participation. Perhaps most importantly, past changes in state Medicaid benefits are likely to have had an impact because almost all AFDC recipients have been automatically eligible for Medicaid. Changes in other programs, such as Food Stamps (FS), general assistance (GA), unemployment insurance (UI), workers compensation (WC), and Social Security Disability Insurance (SSDI) and Supplemental Security Income (SSI) can also have an impact. All of these programs are potential sources of benefits to at least some individuals who might be eligible for AFDC, either directly (e.g., SSI provides benefits for low income adults or children with qualifying disabilities) or indirectly (e.g., GA may provide support to members of an AFDC household who are not in the AFDC family unit, or to a relative of the AFDC family unit who lives in another household, including a non-custodial parent).(3)
2. The Budget Constraint for an AFDC Family
In order to understand how the structure, as well as the benefit value, of AFDC and other programs potentially affect AFDC participation, it is helpful to consider a stylized budget constraint--the trade-off between disposable income and "non-market time" (time spent in activities other than paid employment) -- for the current month that is faced by a single mother who is making the choice between participation and non-participation in that month (Exhibit 1.2).
We treat the value of the combined AFDC and Food Stamp benefit as a single benefit because, from the woman's perspective, a dollar's worth of food purchased with Food Stamps frees up a dollar of cash benefits or other income for spending on other goods and services. Point C represents the value of her combined AFDC and Food Stamp benefits if she does no market work--her maximum monthly benefit (MMB) from the combined programs, sometimes called her "guarantee." If she has earnings, the first dollars earned do not reduce her benefits, and her income increases by one dollar for every dollar earned--along the line segment CI. This ignores payroll taxes (FICA) and the earned income tax credit (EITC), which we will consider later, as well as in-kind benefits such as Medicaid and housing subsidies. At I, a share of each additional dollar she earns is lost through a reduction in AFDC benefits--the marginal benefit reduction rate (MBRR). The MBRR is currently very high--essentially 100% -- in most states. The slope of the line from point I to point D is her wage rate times one minus the MBRR. Point D is the point at which her combined benefits are entirely "taxed" away, and her income at that point is usually called her "break-even income" or "cut off earnings." The slope of dashed line CD is her wage rate times one minus the average benefit reduction rate (ABRR).
Exhibit 1.2
Stylized Budget Constraint for a (Potential) AFDC Family
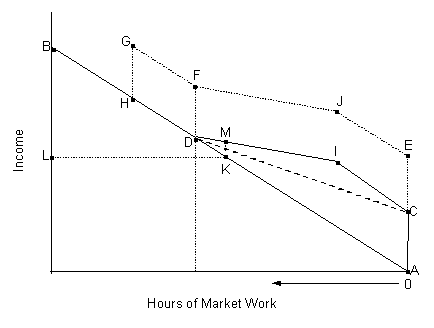
The earnings of some AFDC mothers may reach the "gross income limit" (GIL) before they reach the break-even level. OBRA81 mandated a GIL of 150 percent of the state's need standard; households with pre-benefit income above this amount were declared ineligible for AFDC benefits even if the state's formula otherwise resulted in some benefit; DEFRA84 increased the GIL to 185 percent of the need standard. The GIL only affects the budget constraints of mothers with substantial disregards for work expenses or child care; the GIL has always been above the break-even income level in all states for families with minimum disregards. The effect of the GIL on a budget constraint with high disregards is illustrated by line KL in the exhibit. The level of the GIL is depicted by L. When L is less than the break-even income (the height of D in the diagram), as depicted, the GIL creates a "notch" in this household's budget constraint, depicted by MKD. If the GIL is sufficiently high relative to the cut off earnings of most households, it is irrelevant to the budget constraint.
The stylized budget constraint can be fully described with the wage rate and four "program parameters:" the MMB, the ABRR, the MBRR, and the GIL. That is, the full budget constraint is completely determined by these parameters and the wage rate. We use these parameters, slightly modified, to characterize the budget constraints of an AFDC family with one adult and two children in each state and each quarter of our sample, assuming minimum disregards. Modifications are made for the effects of the EITC and payroll taxes on net income for mothers with earnings, and to capture the fact that the GIL is only relevant to the budget constraint if it is sufficiently low relative to the earnings cut-off of a family with minimum disregards. The EITC and payroll taxes change the rate at which earnings are reduced at the margin, and on average. We take these into account and replace the MBRR and ABRR with the marginal and average tax and benefit reduction rates (ATBRR and MTBRR), respectively. Our measure for the restrictiveness of the GIL is AFDC cut off earnings for our hypothetical household divided by the GIL.
We also attempt to estimate the effects of Medicaid on participation. If the mother receives AFDC payments, she and her children will automatically qualify for Medicaid benefits. In the exhibit, the value of her Medicaid benefit is the distance from point C to point E; point E represents the combined value of her AFDC, Food Stamp, and Medicaid benefits if she performs no market work. Medicaid benefits are not implicitly taxed until her income reaches the "Medicaid need standard" (income at point H); if her income passes that level, she loses all of her benefits. Before OBRA89 the Medicaid need standard was the same as AFDC break-even income in most states. Changes mandated by OBRA89 and OBRA90 expanded Medicaid coverage to individuals with incomes above the AFDC break-even level including pregnant women and children under age six with family incomes below 133 percent of the federal poverty level and children under age 19 with family incomes below 100 percent of the federal poverty level.(4) Thus, given the stylized AFDC budget constraint, two critical parameters determine the Medicaid "add-on" to the budget constraint: the value of Medicaid benefits and the Medicaid need standard. We attempt to capture both of these features in the model, through the use of an estimate of the value of Medicaid benefits to our hypothetical three-person family and a variable intended to capture the effects of the OBRA89 and OBRA90 Medicaid expansions.(5)
All of the following hypotheses are related to the budget constraint and are testable under the methodology:
- Increases in the mother's wage rate (or, more generally, job opportunities) reduce participation, other things constant;
- Increases in the MMB increase participation, other things constant;
- Increases in the ATBRR reduce participation, other things constant;
- Increases in the MTBRR reduce participation, other things constant:
- Increases in the GIL increases participation, other things constant:(6)
- Increases in the value of Medicaid benefits increase participation, other things constant; and
- The Medicaid expansions of OBRA89 and OBRA90 reduced participation.(7)
Changes in these factors have parallel effects on aggregate expenditures. The direction of effects of changes in the parameters on average benefits per person are less clear, however. Even though a change in a parameter that increases the incentive to participate will generally increase the value of benefits received by families that would be participating anyway, it also draws in families that are likely to receive benefits that are below average in value.
3. Other Program Factors
Many states have obtained and implemented waivers to federal rules under Section 1115 of the Social Security Act ("1115 Waivers") during the period under investigation, especially during the last few years, and some were expected to have an impact on program participation. Based on descriptions of all waivers granted during this period provided by ACF, we created a series of indicators for the following features of these waivers: reduction or elimination of AFDC benefits for children born or conceived while the family is receiving AFDC ("family cap"); requirements for participation in work, education, or training activities;(8) extension of transitional Medicaid benefits; elimination of the 100-hour work limitation rule for UP families; and elimination of the work history requirement for UP families.
Many states also enacted laws during the period under investigation that may have had an impact on AFDC caseloads and expenditures. New laws in the areas of paternal identification, child support enforcement, and restrictions on abortion and Medicaid funding of abortions may have affected participation and expenditures through their effects on fertility and family income, in addition to their direct effects on participation.
D. OVERVIEW OF THE MODEL
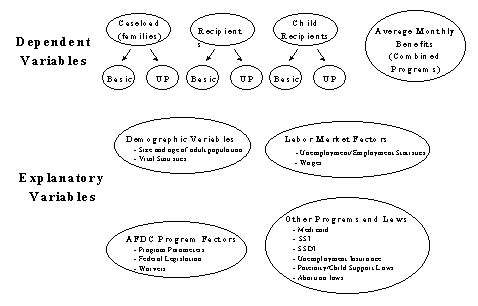
As described previously, the model has six participation equations, three for each program (Basic and UP) and one quarterly average monthly benefit equation for the combined programs. The explanatory variables are classified into four broad groups:
Demographic Factors--We distinguish between two types of demographic factors:
- Size and age distribution of the adult population--we assume that these factors are influenced little by economic factors except through immigration or over very long periods of time. This is clearly true at the national level; changes in a state's economy may trigger changes in these factors, but we assume that current migration induced by current economic change is negligible;
- Family characteristics--the variables used to capture family characteristics are vital statistics (marriages, divorces, and out-of-wedlock births) and immigration measures.
- Labor Market Factors, including the unemployment rate and various measures of employment and wages;
- AFDC program factors, including the program parameters, federal legislation, and state waivers. The program parameter variables partly reflect the Food Stamp program, the EITC, and payroll taxes because these interact with the AFDC program rules to determine the relationship between recipient earnings and net income;
- Other program factors and legislation, including Medicaid, SSI, SSDI unemployment insurance, general assistance, paternity identification laws, child support enforcement, and restrictions on abortions and public funding of abortions.
Most other studies have assumed that the second set of demographic variables, family characteristics, are exogenous to AFDC participation. For the reasons given in the previous section, this assumption may be incorrect. Therefore, we investigate the extent to which this assumption is appropriate in a limited way, by estimating models with and without variables intended to capture the effects of changes in these family characteristics.
A schematic summary of the model appears in Exhibit 1.3
Exhibit 1.3: The Structure of the Model
E. SUMMARY OF THE FINDINGS
1. The estimates we obtain for the effects of the business cycle on participation in the Basic program are substantial, and last longer than any we have found in the literature.
The relationship between the unemployment rate and the AFDC caseload is complex. Current changes in the unemployment rate have lingering effects on caseload growth for many quarters to come. Similarly, current AFDC caseload growth is affected not only by current changes in the unemployment rate, but also by unemployment rate changes from many quarters in the past.
The estimates imply that if the unemployment rate rises by one percentage point and then remains constant for a year, the AFDC Basic caseload by the end of that year will be 2.4 percent higher than it would be if the unemployment rate had not changed. This effect is somewhat larger than the four-quarter effects reported in any previous study.(9)
More significantly, our estimates indicate that a current increase in the unemployment rate affects caseload growth for the next 14 quarters (3.5 years). Previous studies have not found significant unemployment rate change effects after 4 quarters. It appears that we are able to detect these long lags in business cycle effects because we have used the information provided by the individual business cycle experiences of all states over two major cycles.
According to our estimates, if the unemployment rate were to rise by one percentage point and then remain constant for the next 14 quarters, the total increase in the Basic caseload over 14 quarters would be nearly six percent. Of course, this stylized scenario is unlikely. The unemployment rate typically increases by well over one percentage point in a recession, the increase is gradual and erratic, and the peak may be sustained or brief. Below, we describe the estimated effects of the two recessions in our sample period on the caseloads.
We estimate that the poor performance of the economy from 1980 to 1982 resulted in an average annual increase in the Basic caseload of 2.1 percent from 1980 through 1983, and that the sustained recovery that followed reduced the caseload at an average annual rate of 3.3 percent from 1984 through 1989. The impact of the business cycle during this period is not evident in the national caseload, which was essentially the same in 1983 as in 1970 and grew at an average annual rate of 1.0 percent from 1984 through 1989. The reason is that program changes substantially offset the business cycle effects (see below). We estimate that the less severe recession of 1990-91 resulted in average annual caseload growth of 1.5 percent from 1990 through 1993, about 23 percent of the actual average annual growth rate of 6.5 percent. Although the caseload grew by 0.4 percent in the last year of the sample, the recovery from the recession was already having a negative effect, estimated to be 0.8 percent in the last year.
The estimated business cycle effects for the UP caseload are also substantial, and longer lasting than those found previously. According to the estimates, a one percentage point increase in the unemployment rate would increase the UP caseload by 17.3 percent by the end of the year. The effects of a current change in the unemployment rate continue to affect the UP program for 14 quarters, similar to the effects on the Basic program. Based on the estimates, if the unemployment rate increases by one percentage point and then remains constant, the UP caseload would increase by 26 percent after 14 quarters. Cromwell (1986) obtained estimates of a similar magnitude, but after just four quarters. Other studies have found substantially smaller effects. The estimates of the combined effects of the unemployment rate and trade employment per capita are larger.
Again, this hypothetical scenario is unlikely, and we look to historical examples to demonstrate the actual effect of changes in the unemployment rate on the UP caseload. In the 19 states that had UP programs throughout the sample period, we estimate that the poor performance of the economy from 1980 to 1982 resulted in an average annual increase in the UP caseload of 15.3 percent from 1980 through 1983, or about 60 percent of the average annual increase of 25.1 percent. According to our estimates, the subsequent recovery from 1984 through 1989 reduced the caseload at an average annual rate of 16.6 percent, when the actual average annual decline was 7.9 percent. We estimate that the 1990-91 recession resulted in average annual caseload growth of 12.8 percent from 1990 through 1993, essentially all of the average annual growth of 13.1 percent. There was no change in the caseload in 1994, but our results indicate that the recovery was already having a small negative effect, estimated at 0.3 percent.
2. We obtain strong evidence of the effects of changes in three important program parameters--the maximum monthly benefit (MMB), the average tax and benefit reduction rate (ATBRR), and the gross income limit (GIL)--on participation.
We estimate that a ten percent real increase in the MMB (e.g., from $400 to $440) increases the Basic caseload by 2.7 percent and the UP caseload by 2.6 percent. We also estimate that a 10 percentage point reduction in the ATBRR increases the Basic caseload by 1.5 percent, but, somewhat surprisingly, has no impact on the UP caseload. Finally, we estimate that the increase in the GIL enacted under DEFRA84, from 150 percent of the state's need standard to 185 percent, increased both the Basic and UP caseloads by a little over one percent.
Our simulations indicate that the combined effects of program cuts related to OBRA81 reduced the Basic caseload at an average annual rate of 4.6 percent from 1980 through 1983 (mostly in the last two years of that period), more than offsetting the positive effect of the poor economy. The effect on the UP caseload was comparable.
3. The estimated contribution of growth and aging of the at-risk population to AFDC participation was high during the early 1980s (about two percent per year), but declined throughout the period studied.
The reason for the observed pattern is that the youngest members of the baby boom generation--those born in the early 1960s--were entering the age group at highest risk in the early 1980s, while smaller post-boom cohorts were entering that age group by the end of the decade. From 1980 through 1983, we estimate that this factor contributed an average of 2.0 percentage points to annual growth in the Basic caseload. This contribution gradually declined throughout the period and was actually negative by 1994, at 0.4 percent. Results for the UP program were comparable.
4. Legalizations of illegal aliens under the Immigration Reform and Control Act (IRCA) of 1986 appear to have contributed substantially to Basic caseload growth in some states during the period from 1988 to 1993.
Even though individuals legalized under IRCA were not eligible for benefits during a five-year waiting period, many of their children were born in the United States and had been eligible all along, but were apparently not enrolled because of deportation fears. It appears that many "child-only" cases were opened when parents became legal aliens. We estimate that IRCA legalizations contributed about five percentage points to average annual growth in California's Basic caseload from 1990 to 1993, and about 1.5 percentage points to growth in the national Basic caseload.
5. Declines in marriage and increases in non-marital births contributed noticeably to Basic caseload growth throughout the period examined.
These "vital statistic" variables account for average annual growth in the Basic caseload of 0.5 percentage points from 1980 to 1994 which is a little more than one-quarter of the total average annual growth in the Basic caseload of just under 2 percent. We did not find a statistically significant effect for the UP caseload, but this is not surprising because UP cases are two-parent families.
We expected to find that omitting these variables from the models would increase the estimated effects of the labor market and AFDC benefit variables on participation, based on the hypothesis that changes in the latter have an impact on the former. Changes in estimated effects were in the anticipated direction, but proved to be trivial. Thus, it would appear that other major factors are behind the decline in marriage and the growth in non-marital births.
We had originally hoped to develop state-level estimates of female-headed households for use in our models, but our efforts were not successful. Vital statistics variables--marriages, divorces, and non-marital births--were substituted instead. It may be that better measures of female-headed households would lead to stronger estimated effects for this factor, but we do not know.
5. Many other factors we examined were not found to have statistically significant, substantial estimated effects.
We were especially surprised that the Medicaid variables used in the analysis yielded very weak findings, given strong findings that appear in the literature. According to our estimates, the Medicaid expansions for women and children who were not on AFDC had a small positive effect on AFDC caseloads in states where the share of children in AFDC was previously small, and a small negative effect in states where the share of children in AFDC was previously large. We did not find a statistically significant effect for changes in the estimated value of Medicaid benefits.
The following findings are not very strong, and are subject to interpretation. It should be kept in mind that we examined a large number of possible explanatory variables, and any such examination is bound to yield a few "statistically significant" effects by random chance alone.
- States that implemented "family caps"--limits on payments for children born to existing AFDC mothers--under 1115 Waivers experienced statistically significant reductions in their Basic caseloads according to some models we estimated, but not in their UP caseloads. These results are weak and it is not clear what conclusions should be drawn;
- States that imposed restrictions on Medicaid funding of abortions or required parental consent or notification for minors experienced statistically significant reductions in their Basic caseloads according to some models we estimated, but not in their UP caseloads. For abortion restrictions to have a negative impact on the Basic caseload, they would presumably have to reduce fertility among the target population by more than any increase they cause in the number of pregnancies ending in live births. While the findings for the Basic caseload would be consistent with such an effect and are intriguing, they are not rigorous enough to support it on their own. Again, these results are not conclusive;
- Administrative tightening of eligibility requirements for the Social Security Administration's disability programs (Social Security Disability Insurance and Supplemental Security Income) in 1977-78 had a statistically significant, positive impact on the Basic caseload a year later, but not on the UP caseload. As with the other factors described here, it is difficult to know to what extent these findings may be due to chance, or influenced by the effects of omitted variables;
- The share of unemployed persons who are covered by unemployment insurance has statistically significant, positive coefficients in the Basic participation equations. The sign is contrary to what might be expected, and may reflect factors that have been omitted from the model and that have positive effects on both participation and the share of unemployed persons who are insured; and
- The number of children receiving SSI benefits also has significant, positive coefficients in the Basic participation equations. The explanation of the counter-intuitive sign of this coefficient may be similar to that for the coefficient of the insured unemployment variable.
Other factors we tried that did not yield statistically significant findings are: average weekly wages in the trade industry; average weekly wages in manufacturing; total employment per capita; manufacturing employment per capita; dummy variables for other types of 1115 waivers (in addition to family caps); dummies for child support and paternity establishment laws; the ratio of employed men to the number of women of childbearing age; dummies for the existence and type of UP program (Basic participation equations only); a measure of cuts in state general assistance programs; SSI benefit levels, including state supplements; and the number of SSI children in the Zebley class.(10)
In many years, the changes in the state explanatory variables in the models account for most of the observed changes in the caseload, but there are important exceptions. We included "year effects"--dummy variables for each year to capture the average effects of omitted, or poorly measured, factors on the Basic and UP caseloads. For both caseloads, the coefficients are positive in most years and are statistically significant from 1985 to 1991, indicating that factors other than those captured in the state explanatory variables played a substantial role in determining caseload growth. For the UP caseload, the dummy coefficients are also positive and significant in 1980 and 1981. Possible reasons for these positive year effects include:
- Effects of federal legislation that applies equally to all states;
- Overestimation of the impact of the recovery from 1983 to 1989, and underestimation of the impact of the recession of 1990-91;
- Effects of the relative decline in wages for low-skill work;
- Underestimation of the contribution of immigration;
- Underestimation of the role of changes in household characteristics;
- Increases in the cost of health care and reductions in access to health insurance that were not captured with our Medicaid variables; and
- Declines in job prospects for low-skilled workers that are not reflected in the unemployment rate and/or the trade employment variable.
F. RESEARCH IMPLICATIONS
This study demonstrates both the promise and limitations of the pooled time-series approach to studying AFDC caseload participation, other state-level measures of program participation, welfare, and health. We have obtained what we believe to be the most accurate estimates of the effects of labor market factors on AFDC participation of any study to date,(11) and have also obtained strong findings for program parameters.
At the same time, however, we have not been able to reliably estimate the effects of several state-level factors that are believed to be important determinants of AFDC participation. While we obtained strong results for non-marital births and marriages, we do not know the extent to which these variables capture the effects of growth in female-headed households, which we could not measure satisfactorily at the state level. Other determinants to consider further are other characteristics of families, access to health care insurance, the value of Medicaid, wages in low-skill jobs and other aspects of local labor markets not captured in the current model, other aspects of immigration, and parameters of other programs (e.g., UI). Further progress in this area will require development of better measures of state-level variables.
Recent caseload declines and devolution have substantially heightened interest in measuring and understanding the determinants of the welfare and health of vulnerable populations at the state level as well as of program participation. The pooled time-series approach to modeling these variables at the state level may prove to be a useful tool in helping researchers and policymakers determine whether changes in such variables are due to state program changes or to environmental factors that are beyond the control of the states. The promise of this tool will be substantially enhanced if better measures of key state-level factors are developed--both prospectively, as welfare reform and other changes occur, and retrospectively, as is necessary to estimate and understand the impacts of these factors on the measures of interest.
The value of this tool will also depend, however, on the extent to which states vary in their approaches to welfare reform. While the AFDC program varied substantially across states during the sample period, it was still reasonable to say that there were 51 variants of the same program and to analyze them together. Reforms may be so radical and varied as to make such a statement unreasonable in the future. Over time, pre-devolution caseload behavior will become less and less relevant to post-devolution caseload behavior.(12)
G. FUTURE WORK
This effort has produced some important findings, but has also fallen short of its objectives in some respects. Future work that would build on the findings of this project may benefit from the following recommendations.
1. Refinement of the "expected participation" variables should be considered. The single most important explanatory variable in the participation model is the change in the logarithm of our "expected participation" measure. This measure is a weighted sum of the number of women in the state in age groups that are at-risk for participation, with weights equal to national participation rates by age-group in 1990 (see Chapter 3). This variable is intended to capture the size and age distributions of the population of women who are at-risk for participation. Michael Wiseman has suggested that the widening over the sample period between actual caseloads and predicted caseloads is in part due to the fact that this is an index with weights fixed by observed participation rates in one year. An alternative would be to compute the change for each state in each year using weights based on national participation by age group in the previous year--i.e., to update the weights when computing each year's change.(13) Obtaining different weights for each year from SIPP may be problematic, but it should be possible to obtain weights for many other years. An even more desirable solution would be to use each state's own age-specific participation rates in the previous year to predict the change in participation due to population change, but the information needed to construct state-specific indices is not available.
2. Development of models with alternative dependent variables should be considered. Possibilities include:
- Openings and closings--we initially considered using case openings and closings as dependent variables, but elected not to in keeping with the mainstream of the existing literature and because of concerns about the openings and closings data. The extra effort needed to estimate such models given the existence of the database for the explanatory variables is small, however, and might well pay off.
- Disaggregated dependent variables--the ACF participation data are reported by program (Basic vs. UP), and cannot be directly disaggregated further. It might be possible, however, to use the ACF quality control (QC) data to estimate disaggregated caseloads. We think that disaggregation by citizenship, reason for deprivation, child-only vs. other, ethnicity, age, or sex of household head would be especially helpful if feasible. Disaggregation by state regions might also be very useful. Reviewers have provided three examples of how caseload behavior in some regions within states have varied substantially from those for the rest of the state.(14)
- Aggregated dependent variables--we developed separate participation models for the Basic and UP programs, but it may be that the separation of the two programs created some problems for the analysis. We have learned, for instance, that a large share of UP cases in California eventually convert to Basic cases. Such conversions might help explain caseload growth in the Basic program during the 1984 -1992 period following the large increases in the UP program during the earlier recession. While this could be modeled directly, it may be problematic to build models in which lagged participation measures for one program appear as explanatory variables in participation models for the other. Combining the caseloads and estimating a single model may be a more useful alternative.
- Joint AFDC/SSI models--we attempted to estimate the effect of changes in SSI child recipients on AFDC caseloads, but were not successful. The likely reason is that participation in both programs is, in part, determined by a common set of factors. It might be fruitful, instead, to develop models of "welfare recipients," including those on either AFDC or SSI. We think it would be feasible to develop a model for AFDC or SSI child recipients, and another for adults age 15 - 64. The adult model could be substantially improved by separating female and male recipients; this is possible for the SSI recipients, but may not be possible for the AFDC recipients--depending on the QC data. Garrett and Glied (1997) have pursued this approach.
- Alternative functional forms for the participation variables--we used the logarithm of the participation variable or the log of participation rates. The logarithmic specification implies that a change in an explanatory variable is proportional to the level of participation. Use of the level of the participation rate (caseload per adult in the relevant age group, say) is a defensible alternative.(15) We have noticed that several states with relatively small UP caseload rates at the beginning of the sample period experienced extraordinarily large percent age increases in their UP caseload rates in the first three years of the sample period relative to the percent increases observed in other states; the percentage point changes in the caseload rates themselves, however, are much more comparable to those in other states. (16)
3. Development of additional explanatory variables should be considered. Possibilities include:
- Wages for low-skill workers--one promising explanation of growth that is not accounted for over the sample period is the relative decline in wages for low-skill workers. Substantial research has been done by labor economists on understanding the causes of this decline, and some of that work has been done using state or regional data. Several economists familiar with this research have suggested that, with some effort, reasonably accurate state-level estimates of wages for low-skill workers could be constructed, following work that has already been done in this area.(17) We did not pursue this under the current project because of the level of effort required;
- Unemployment insurance benefits--Dr. Jonathan Gruber (MIT) has developed a computer model for simulating UI benefits to workers with specified characteristics in each state for every year since 1968. This model could be used to construct a measure of each state's benefits that would be analogous in origin to the AFDC program parameters we used in our research. This would be a better measure of the generosity of the state programs than the UI measure we used in the estimates reported here;
- Immigration variables--we have not included a variable for refugees in our models. Even though the number of refugees is small, high participation rates among refugees may mean that they are an important explanation of caseload growth in some states. More generally, the strength of our findings for IRCA legalizations suggests that more effort in modeling the effects of immigration on caseloads may be fruitful;
- Female headed households--our efforts to produce state-level estimates of this explanatory variable were not very successful. We found that even subregional estimates based on the March CPS exhibited substantial random variation from one year to the next. We have not had time to examine the reasons for this variation--whether it is just sample size or whether it might be some other aspect of the CPS methodology. It may be that better estimates can be produced, but significant effort will be required to determine how this might be done. Ongoing efforts by ASPE and others to develop state-level estimates of many health and welfare indicators may prove useful here;
- Medicaid measures--we were surprised not to find more significant findings for the Medicaid variables we tried. It is puzzling that previous analyses of micro data have produced much stronger results. A substantial effort to understand the reason behind these inconsistent findings might produce better measures for use in the state-level analysis;
- Neighbor variables--Shroder (1995) used measures of labor market and AFDC program variables in neighboring states in his models. We did not have the time to construct such variables for this project, but they can be constructed from the data we have already assembled. Given concerns about states "racing to the bottom" under devolution, it may be especially valuable to examine how reductions in benefits in one state affect caseloads in neighboring states;
- Minimum wage--we did not include the minimum wage in our models. Most states use the federal minimum, but some states have had higher values in at least some years. A recent analysis by Burkhauser, Couch and Wittenburg (1996) of the effect of minimum wage increases on employment of "at-risk" youth in 1990 and 1991 suggests that this would be fruitful.
4. Simultaneous models of benefit levels and program participation should be considered. Shroder (1995) found much stronger results for the impact of increases in benefits on participation when he modeled them as simultaneously determined with participation levels. As he and others have argued, an increase in the burden of a state's welfare expenditures on taxpayers is likely to make cuts in benefits politically popular; i.e., higher participation results in legislated reductions in benefit levels. This negative, reverse relationship between benefits and participation may result in an underestimate of the presumably positive effect of benefits on participation. We are, however, concerned about the quality of possible instrumental variables needed to identify the effects of benefits on participation, especially because there are three benefit variables that would require instrumentation.(18) Three instruments would be required at a minimum, and all three would need to be important determinants of the benefit parameters that do not have a direct impact on program participation. Additional resources would be needed to pursue this further.
5. Extension of the sample period should be considered. Data for the participation variables in our model are available from the fourth quarter of 1974 on. Data through the end of the federal program (third quarter of 1996) should soon be available. The sample period constraints we faced primarily came from the explanatory variables. Earlier and, especially, later data for many key variables can, however, be obtained or constructed, but may require substantial effort.
6. Further examination of the stability of the parameter estimates across subperiods should be considered. We were limited in our ability to produce subperiod estimates by both resources and software. More effort in this area would be helpful in determining whether changes in the program or the characteristics of participants have affected the sensitivity of participation to the business cycle, program parameters, or other factors. For instance, the introduction of the UP program could have reduced the sensitivity of participation in the Basic program to business cycles.(19) Other major programmatic changes that occurred during the period under investigation could have had similar effects--especially the provisions of OBRA-81 and the introduction of JOBS.
7. Further examination of asymmetries in business cycle effects and, more generally, model dynamics should be considered. Many have suggested that the effects of business cycles on the caseload are asymmetric, with rapid growth during recessions and only gradual declines during recoveries. We explored this idea by estimating models with different distributed lags for unemployment in growth and recession periods, but found only very small, insignificant differences. Such models are known as "switching regression" models, with the applicable specification for a period depending on some decision rule. Our models were crude in this respect, with the applicable regression depending on whether or not the national unemployment rate was increasing in the current period. Steven Thompson recently developed a more sophisticated version of a switching regression model for his monthly time-series model of Maryland's caseload, with some success in identifying asymmetric effects (Regional Economic Studies Institute, 1994). Maryland's caseload (see Chapter 6) displays a pattern of rapid increases after recessions and gradual declines during the following recoveries. Thompson's initial experience was similar to our own; using the change in the current national or regional unemployment rate yielded results that did not seem to capture the asymmetric relationship very well. After some experimentation, however, he discovered that lagging the "switch" from the recession model to the recovery model by 8 to 12 months after the peak in the caseload yielded a much better fit for Maryland. We do not know whether a similar lag would fit other state experiences well.
Another reviewer, Michael Wiseman, has suggested developing a dynamic model in which the speed of adjustment of the caseload depends on the difference between the actual caseload and a long-run equilibrium level. Such a model would put a different structure on the lagged variables and include the lagged caseload variable as an explanatory variable. This seems to be echoed, but with a twist, in the comments of a third reviewer, Don Winstead, who suggests that lack of program capacity to deal with the large numbers filing for benefits during the Florida recession resulted in larger caseloads than would have been realized had capacity been greater.
Don Winstead also suggested that changes in the unemployment rate lag, rather than lead, caseload changes in a recession, but lead them in a recovery. The theory is that low-skill workers are the first fired in a downturn and last hired in a recovery.
8. More extensive analyses of actual and predicted series in individual states might be useful. The independent reviews of our findings for four selected states were useful in both understanding growth in those states and understanding the strengths and weaknesses of the model. We did not have an opportunity to revise the model to incorporate information we obtained from these reviews, but this would be feasible. For instance, Steven Thompson reported that he found a substantial interaction in his time-series model between an 1115 waiver for the "Up-Front Job Search" program and labor market variables. The estimated coefficients of the labor market variables increased substantially after the program's implementation. This essential elements of this specification could be implemented in the pooled model. Detailed assessments for additional states might also be very useful.
Notes
1. An important limiting factor in applying the methodology to indicators of well-being is that reliable state-level measures of many indicators do not exist. ASPE and others are promoting efforts to improve measurement of state-level indicators going forward, but these will not be helpful for supporting the type of modeling reported on here until at least several years into the future. Existing data may permit development of reasonably reliable estimates of some state-level indicators retrospectively.
2. A few recent studies have found evidence that suggests business cycles impact family structure. Moffitt (1994) includes the state unemployment rate and variables reflecting employment in specific sectors in his study of female headship that uses pooled CPS data from 1968 to 1989. Unemployment was significantly and positively related to female headship among black females, but not among white females. Blank and Ruggles (1996) include the state unemployment rate in duration models of AFDC eligibility and AFDC participation. Unemployment reduces the likelihood that a spell of AFDC eligibility will end due to a change in family composition. However, Moffitt (1995) finds little consistent evidence that AFDC benefits have had a substantial impact on out-of-wedlock childbearing.
3. Throughout this document we use the word "family" to refer to AFDC assistance units, as defined by Federal and state regulations, although some units contain individuals who are not legally related to each other.
4. This second requirement is currently being phased-in and holds true only for those children born after September 30, 1983.
5. We are grateful to Aaron Yelowitz for providing the Medicaid expansion variable. See Yelowitz (1994).
6. Note that "other things constant" implicitly includes the AFDC earnings cut-off, which is fully determined by wages and the other program parameters.
7. See Yelowitz (1994) and Moffitt (1992) for more complete discussion of these theoretical points.
8. This refers to requirements that are beyond those of the state's JOBS program.
9. Cromwell, et.al, (1986) found that the same change results in a 1.8 percent caseload increase after a year, using a similar methodology. The Congressional Budget Office estimates a 1.7 percent increase using a time-series model (CBO, 1993). The findings we report here are based on a model that uses changes in the unemployment rate as the only labor market variable. Adding another business cycle variable, trade employment per capita, essentially increases the estimated effect of the business cycle.
10. Since completing this work, we have become aware of very recent analyses of the impact of Zebley on SSI child participation and the share of SSI child participation growth accounted for by transfers from AFDC, by Garrett and Glied (1997). There preliminary results indicate that about half of the SSI child growth caused by Zebley is accounted for by transfers from AFDC.
11. Hoynes (1996) has also obtained strong and convincing results in a duration analysis of AFDC cases in California, using local labor market variables.
12. Tom Corbett is more pessimistic. In correspondence to us, he writes: "The reality is that the notion of a national program where a few relatively easily measured economic, demographic, and program parameters could predict caseload had virtually disappeared by the 1990s."
13. The problem is analogous to the problem with fixed weight price indices, such as the Consumer Price Index, which become a poorer and poorer measure of inflation as actual consumption bundles drift away from the market basket used to determine the weights. The proposed solution is equivalent to a Divisia ("chain-linked") price index.
14. The examples are California (northern vs. southern), Florida (Dade County -- Miami area -- vs. the rest of the state), and Maryland (Prince George's County vs. the rest of the state).
15. Another way to define the participation rate in a state would be to divide the caseload by a weighted sum of the population in various age groups, using national participation rates by age in a base year as weights. We use the logarithm of this denominator, which we call "expected participation" as an explanatory variable in our participation models.
16. For example, Nebraska's caseload increased by 260 percent from 1979.4 to 1980.4, but the base was very small (60 families) and the per capita increase was high, but not out of line with the experience in other states during the period.
17. Steven Thompson reported that Regional Financial Associates in West Chester, PA, has obtained data from state employment departments for all 50 states. We had previously explored wage data available by state and industry from the Department of Labor and determined that data for specific low-wage, low-skill industries were missing in many states and many years.
18. We originally had planned to estimate a simultaneous model for the maximum monthly benefit variable, following Shroder (see Lewin-VHI, 1996), but abandoned this effort after expanding the number of benefit parameters in the model. One idea for generating instruments is to use the share of adults (voters) in various age groups; presumably elderly voters are less supportive of benefits for young families than are younger voters. Another possibility is the Federal share of the AFDC payment; the higher the Federal share, the less would be the impact of a change in the caseload on taxpayers.
19. Testing whether the presence or absence of an UP program shifts the parameters for the Basic model merits further discussion because there are really three separate regimes to consider. All States have been required to have UP programs since October of 1990, and this period clearly represents one regime. Many States adopted UP programs voluntarily well before 1990. Pre-1990 observations for these States could be grouped with post-1990 observations for all States, but the fact that these States had voluntary programs, along with the fact that these State programs did not necessarily comply with Federal rules that came into effect in 1990, makes it possible that these two groups of observations are not comparable. Hence, we will begin by treating them as separate regimes. Observations for States with no UP programs constitute the third possible regime. For this study we examined the comparability of results for the UP programs across the first two regimes in an informal way.
CHAPTER TWO: REVIEW OF THE LITERATURE
A. INTRODUCTION
In this chapter we review relatively recent AFDC participation studies. This includes a discussion of the merits and limitations of the various econometric methodologies that have been used to study AFDC participation previously, as well as an examination of the dependent and independent variables used in the studies.
The following five methodologies, or methodological groups, are considered:
- Time-series analysis of national aggregate data;
- Time-series analysis of state aggregate data;
- Pooled (cross-section time-series) analysis of state aggregate data;
- Analysis of cross-sectional and longitudinal (panel) data for individuals; and
- Analysis of pooled (cross-section time-series) data for individuals.
An important conclusion is that the pooled analyses of aggregate state data -- the method we used in this study -- holds substantial promise relative to alternative methodologies, but also has some limitations.
In Sections B through F we describe recent studies in each of the respective methodological categories. We review program participation measures used in these studies in Section G and explanatory variables in Section H. Conclusions drawn from this literature that have influenced the specification of our model appear in Section I.
B. NATIONAL TIME SERIES
In national time-series models, regression analysis is used to estimate a relationship between some measure of program participation (e.g., the average caseload) in the entire country over some time interval (usually years or quarters) to a set of explanatory variables that represent or serve as proxies for hypothesized determinants of growth.
The Congressional Budget Office model (CBO, 1993) is the most recent national time series model that we have found.(1) We describe this model in some detail below and use it to provide context for a discussion of the strengths and weaknesses of this methodology. We then go on to describe briefly one earlier national time-series model.
The CBO model uses quarterly data for the period from 1973.1 through 1991.3 (73 quarters). Separate models are estimated for the Basic and UP caseloads.(2) For each model, the dependent variable is the average monthly caseload over the three months of the quarter. specifies the caseload measure as a linear function of a set of explanatory variables and a disturbance term. The disturbance term represents all determinants of the caseload that are not captured by the explanatory variables, and is assumed to change slowly over time.(3)
Explanatory variables include: a measure of female-headed families, used in the Basic equation only;(4) the "employment gap" -- the difference between actual and potential employment; a measure of the real average (across states) maximum AFDC benefits for a family of three; average earnings for year-round, full-time workers aged 18 to 24 with exactly 12 years of schooling (a female series is used for the Basic model and a male series is used for the UP model); three dummy variables to capture the transitional and permanent effects of program changes enacted under OBRA81; and three quarterly dummies to capture seasonal caseload variation. The real earnings data are annual data that have been converted to quarterly data by interpolation. Both current and lagged values of the employment gap variable are included in the equations; the first through third lagged values appear in the Basic equation and the first through fifth lagged values appear in the UP equation.
Almost all of the coefficients reported are statistically significant, and the few that are not have the expected sign. The most significant variables (i.e., those with highest t-statistic for their coefficient) in the Basic equation are the measure of female-headed families, and two of the three OBRA81 dummies. The four employment gap variables (current and three lags) are collectively very significant as well. In the UP equation, the first and second quarter dummies have the most significant individual coefficients. Collectively, the six employment gap variables (current and five lags) also stand out as especially significant.
For purposes of comparison with other studies, we used the CBO results and ancillary data reported by CBO to compute the estimated effect of a one percentage point change in the unemployment rate on the Basic and UP caseloads. Because the employment gap, rather than the unemployment rate, is included in the CBO model, it was first necessary to investigate the relationship between these two variables. Based on data reported in Figure 6 of CBO (1993), it appears that a one percentage point change in the unemployment rate is approximately equivalent to a one percentage point change in the employment gap variable. Given this, and assuming that the initial unemployment rate is five percent, the CBO estimates imply that a one percentage point increase in the unemployment rate increases the Basic caseload by 1.7 percent after four quarters and increases the UP caseload by 9.7 percent after six quarters.
There are numerous advantages of the national time-series methodology relative to others, but there are also significant disadvantages. We use the CBO study to illustrate some of the advantages and disadvantages, but they apply to other national time-series studies as well. The advantages include:
It is methodologically simpler than most other approaches. This makes it relatively easy to apply, and the results are relatively easy to describe.
National data for explanatory variables are readily available from published sources. Further, national explanatory variables are available at a level of specificity and measured with a degree of accuracy that is not available for smaller geographic units such as states. Most of the data used by CBO come from readily available published sources.
The researcher can examine the dynamics of the relationship between explanatory variables and participation, as CBO does by including both current and lagged values of the unemployment rate. This cannot be done with a pure cross-section approach, which uses data from only a single point in time.
In a statistical sense, the researcher is able to "explain" a very high percentage of the variation in participation over time (high adjusted R-square) and to produce simulated participation series that closely track the actual series. This is true of CBO's models -- the adjusted R-squares are 99.6 percent and 99.5 percent for the Basic and UP equations, respectively, and sample-period simulations track the actual series well. This occurs because time-series data -- especially aggregate data over large populations -- tend to be very highly correlated with one another. With a small to moderate size sample, such as CBO's, it is fairly easy to find a small set of explanatory variables that can achieve a good fit. There is, however, a negative aspect to this advantage, which we return to later.
The disadvantages of the national time-series approach include:
It can capture state-level changes in AFDC programs only in a very crude way -- through their impact on program variables that are aggregated across states, such as CBO's AFDC average maximum benefit for a family of three. The authors of the CBO report note that this variable may be endogenous: as caseloads increase, states may cut back maximum benefits for budgetary reasons (CBO, 1993, p.39).
The method's ability to distinguish between the effects of a substantial number of variables is limited by high correlations among explanatory variables that are typical of time-series data, and by limited observations. For instance, it is difficult to be confident that the impact of an increase in unemployment ends after three quarters for Basic and five quarters for UP given the likely high correlations among the various lags of the unemployment rate and the relatively short time-series available for estimating CBO's model. The authors mention this as a specific problem with their model (CBO, 1993, p. 12).
Major national-level changes in the program are difficult to disentangle from the effects of other variables because they can usually only be modeled in a very crude way -- such as the three dummy variables that CBO used to capture the impact of OBRA81. The authors of the CBO report mention this as another specific problem with their model (CBO, 1993, p.12). This same problem would arise in modeling the impact of the 1988 Family Support Act (FSA) using more recent data. Both OBRA81 and the FSA may be viewed as changes in "regime," and it could be that coefficients of other variables also changed with the regime shift. When regime shifts occur as frequently as they perhaps have for AFDC, time-series data alone are likely to be inadequate for testing whether other coefficients did change. For instance, using national time-series data we would be unlikely to determine whether the mandating of the UP program as of October 1990, under the FSA, had an impact on the models other than a one-time shift in UP participation.
There is a serious danger that the researcher will end up with a model that fits the data well (very high adjusted R-square and the simulated series tracks the actual series closely), but that the model coefficients misrepresent the causal relationship between the explanatory variables and participation; further, out-of-sample predictions may be very poor. The reason is that the high correlations found in time-series data, combined with a fairly small sample size, make it relatively easy to get a good fit by trying a variety of different specifications or by constructing an explanatory variable that seems to track participation well but that does not have a clear theoretical rationale. CBO's measure of female-headed households (FHH) may be such a variable.
The last point merits further discussion. According to the report, the FHH variable is defined as the "number of families headed by women with their own children under age 18, multiplied by the ratio of never-married mothers to mothers who had been married." This variable was developed after an attempt to include separate variables for families headed by never-married mothers and by ever-married mothers led to nonsensical results, evidently because of multicollinearity between the two variables (CBO, 1993, p. 14, fn. 17). Although the particular functional form used to aggregate the variables does not have an apparent theoretical rationale, the path of the variable has an upturn that coincides with the upturn in Basic caseload growth.
While the variable is critical to the fit of the model, the authors find that its coefficient is implausibly large; the coefficient implies that 80 percent of all new female-headed households move onto AFDC (CBO, 1993, p. 18). The authors suggest that some of the growth attributed to this variable may be due to omitted factors, such as the Immigration Reform and Control Act of 1986 and Medicaid outreach.
Other than earlier versions of the CBO model, the next most recent national time-series model we have found comes from ASPE's last effort to model AFDC caseloads (Grossman, 1985). This effort is notable because the author also explored the development of a pooled, state-level model, and contrasted the findings to the findings from a national time-series model. We describe the national model here, and return to the state-level model in Section D, below. The national model also provides additional examples of the advantages and disadvantages of the national time-series approach.
The Grossman model is estimated with quarterly data for the period from 1974.4 through 1983.4 (37 quarters). The Basic and UP programs are modeled separately. Two equations are estimated for each program: a caseload equation and an average benefits per case equation. The primary purpose of this effort was to improve national forecasts of AFDC expenditures for each program (the product of the program's case-load and average expenditure per case).
As in the CBO model, the caseload measure for each program is the average caseload over the three months of the quarter. The average benefit variable is the average of the monthly values for benefits per case over the same three months.
Explanatory variables in the Basic caseload equation include: the number of female-headed households, the poverty rate for families, the real average hourly wage rate in retail and service industries, the average standard of need for a family of three, the lagged unemployment rate (with lags for four quarters), quarterly dummies, and three dummies to capture the transitional and final impacts of OBRA81.(5) The explanatory variables in the UP caseload equation are the same except that the labor force in UP states replaces the number of female-headed households and the fifth lag of the unemployment rate is added. A first-order autoregressive disturbance is specified for each model.
Note that the CBO (1993) caseload specifications are very similar to Grossman's specifications in many respects. The variables with the most significant coefficients are the OBRA81 dummies and the female-headed household variable. The only variable with a very insignificant coefficient (t-statistic less than 1.0) in both equations is the poverty rate. As with the CBO model, adjusted R-squares are very high: 97.5 percent for the Basic caseload and 99.0 percent for the UP caseload.
The implied long-run elasticities for the Basic and UP caseloads with respect to the unemployment rate are very similar to those calculated from CBO's findings: 0.1 for the Basic caseload (identical to the value we found for CBO) and 0.7 for the UP case-load (compared to 0.5 based on CBO's findings), despite the fact that only about half of CBO's sample period was used by Grossman.(6) Thus, it appears from the national time-series estimates that the impact of a change in the unemployment rate on caseloads has been reasonably stable over a long period of time.
The average benefit equation for the Basic program includes the following explanatory variables: the weighted average of the maximum benefit for a family of four, an estimate of the average number of persons per family in the United States, and dummy variables for OBRA81. The average benefit equation for the UP program also includes the maximum benefit variable and an OBRA dummy, but does not include the average family size variable. The adjusted R-squares for both equations are very high: 99.4 percent for the Basic equation and 98.6 percent for the UP equation. The maximum benefit variable has a very large t-statistic in both equations, and accounts for most of the models' explanatory power.
We note that Grossman did not include the unemployment rate in the average benefit model. Holding the maximum benefit constant, increases in unemployment may be associated with reductions in earnings among existing recipients, which would increase average benefits. Earnings and other benefit determining characteristics of cases that enter the caseload due to an increase in unemployment may differ from those of existing recipients. This could offset or add to the hypothesized positive effect of unemployment on average benefits for existing cases.
C. INDIVIDUAL STATE TIME SERIES
1. Overview
Most states have developed their own AFDC caseload forecasting models, which are typically used for budget and staffing projections. A 1990 study conducted by the state of Oregon documents the variety of techniques used by the fifty states in forecasting their AFDC caseloads (Oregon State Department of Human Resources, 1990). According to this study, most states use a simple trend analysis (fitting a linear relationship to past series of caseload values) to predict future values for the AFDC caseload. Several states, however, use a multivariate regression framework, incorporating demographic, economic, and programmatic factors, to forecast their AFDC caseloads.
We reviewed state models for two reasons. First, individual state models may reveal important determinants of the AFDC caseload that have not been examined in other studies. Second, our plan called for using the model we developed to simulate caseload series in a few selected states. For this analysis, we wanted to select states that have well-developed AFDC models so that we could compare the results of our model to findings from the state models. In addition, we expect that the developers of the state models would be helpful in interpreting our findings.
The state models discussed here provide additional examples of how particular factors may be measured and incorporated in our model of caseload growth. The models also identify important state-specific policy changes that occurred during the time period we will examine. The MinnesotaCare program in Minnesota and the FIP program in Washington are examples. To the extent that such policy changes are identified, they can be included in our model of caseload growth. Given the fact that we will not be able to identify all such policy changes for all states, the state models that do provide information on policy changes will allow us to test the sensitivity of our results to the omission of state-specific policy variables.
Below, we describe selected state models that go beyond trend analysis or ARIMA models(7), incorporating factors believed to influence AFDC caseload growth in a multivariate regression framework. The models we describe are those used by Florida, Maryland, Minnesota, Oregon, Texas, and Washington. In addition, we discuss a report by Barnow (1988) that presents a guide for states to use in developing their own AFDC caseload models, using New Jersey as an example.
2. State Models
Barnow (1988), in a study conducted for ASPE, developed a guide for states to use in constructing models to predict AFDC-Basic and UP caseloads. Models were developed using the state of New Jersey as an example, spanning the period 1978 to 1985. In these models, the quarterly AFDC caseload is regressed on: the number of divorces, the real average weekly wage in the retail trade industry, the number of persons unemployed in the state, out-of-wedlock births, the total state population, a set of dummy variables representing permanent and phase-in effects of OBRA81, a dummy variable representing the implementation of the 1984 Deficit Reduction Act (DEFRA), a set of seasonal dummy variables, and a set of variables interacting OBRA with the divorce, unemployment, wage, and out-of-wedlock birth variables. Many other variables were tested but not included in the final models. These include the need standard, the number of marriages, employment in the retail industry, earnings in the personal services industry, and the number of persons who have exhausted their Unemployment Insurance benefits.
Florida
Several governmental entities in the state of Florida employ statistical models to forecast the state's AFDC caseload. The Governor's office utilizes an OLS regression framework combined with ARIMA modeling techniques to forecast AFDC caseload and costs. Explanatory variables used in the models include the female population ages 15-45 and the unemployment rate. The Legislature bases its forecasts on a multivariate regression model using quarterly data from 1981 to the present. The dependent variable is the average monthly AFDC caseload, seasonally adjusted. Explanatory variables include the state unemployment rate (seasonally adjusted), the state female population ages 18 to 44, and a dummy variable accounting for policy changes occurring after 1987. In the past, the regression equation has included a variable representing movement in and out of unskilled labor (e.g., labor in the retail trade).
Maryland
The Maryland AFDC Net Flow Model is one component of a larger, macro model of the Maryland economy. Models are specified separately for the AFDC-Basic and AFDC-UP caseloads. The AFDC-Basic model is specified as a log linear model where the number of paid cases is a function of the unemployment rate for the at-risk population, a measure of real net income gain from work, the size of the at-risk population, an index of help wanted ads, and the rate of AFDC case closings. The at-risk population is defined as female headed households with children under age 18. The real net income gain from work is the real average monthly wages after taxes minus the real monthly combined value of AFDC, food stamp, and Medicaid benefits.(8) Explanatory variables used in the AFDC-UP model include the unemployment rate, an index of leading economic indicators developed by the state, the index of help wanted ads, and a lagged value of the UP caseload.
Minnesota
The Minnesota model uses monthly time-series data to forecast AFDC-Basic and AFDC-UP caseloads, specifying a structural component and an ARMA component in the model. The AFDC-Basic structural component includes variables for unemployment (including lags), out-of-wedlock births, the real payment standard for a family of three, and the number of families with children enrolled in Minnesota's publicly-subsidized health insurance program, MinnesotaCare. MinnesotaCare is believed to have an impact on AFDC caseloads because it offers an affordable alternative to Medicaid should an AFDC recipient have an opportunity to take a job that does not offer health insurance benefits. This variable has proven to be a statistically significant predictor of Minnesota's AFDC caseload. The AFDC-UP model uses the same variables as those used in their AFDC-Basic model, except that in-wedlock births are used instead of out-of-wedlock births.
Oregon
Oregon uses a multivariate regression model to forecast caseload growth where the number of AFDC cases is a function of the fertility rate of unwed women, the female population ages 15-44, the number of divorces, the real value of the average AFDC cash grant to a family of three, the federal poverty level for a family of three, and the total number of births. The data for this model are monthly, but the model is used to produce annual forecasts. Oregon projects four years into the future. For the nine years previous to 1994, the Oregon model consistently produced R-squares of over 90 percent. In 1994, however, the State of Oregon's AFDC policy changed from one of eligibility determination to one of diversion. That is, the Department of Human Resources first seeks ways to keep individuals/families off AFDC by primarily helping parents keep their current jobs or find new adequate employment. As a result, the explanatory power of the model has dropped significantly because the model does not contain a variable that captures this important policy change.
Texas
One of several models used by the state of Texas is a multivariate regression model where the dependent variable is the number of AFDC-Basic cases. The model's explanatory variables include: the number of separated/divorced female-headed households with children under age 18; the number of never-married female-headed households with children under 18; the combined (inflation adjusted) cash value of monthly AFDC, food stamp and Medicaid benefits for the typical three-person AFDC family; the average (inflation-adjusted) wage rate in the retail sector; the gap between 'full' and actual nonagricultural employment; and a dummy variable representing the implementation of the JOBS program in the fourth quarter of 1990. Increases in the caseload have been attributed to the JOBS program; however, staff at the Department of Human Services believe there is a crossover effect due to recent expansions in Medicaid eligibility, and that new Medicaid applicants are also being found to be eligible for AFDC.
Washington
Washington uses entry and exit models to project AFDC caseloads. The state uses separate models to forecast AFDC-Basic and AFDC-UP caseloads. In both models, a month's caseload is equal to the previous month's caseload plus projected entries minus projected exits. Apparently, the models were quite successful in forecasting caseload changes until 1994, when reforms began to reduce caseloads.
The AFDC-Basic entry model regresses the entry rate (new entrants divided by the population of males less than age 19 and females less than age 49 not on AFDC) on the out-of-wedlock birth rate, seasonal dummy variables, and a reform status variable representing the impact of the Family Independence Program (FIP) initiated by Washington in 1988. The reform variable measures the weighted percentage of state community service offices operating under FIP or FSA.(9) The AFDC-Basic exit rate model regresses the exit rate (exits divided by the Basic caseload) on: the ratio of the three-person grant to typical earnings in non-manufacturing employment; the gap between the employment rate and its previous maximum, where the employment rate is the ratio of total non-agricultural employment to number of Washington residents between the ages of 18 and 64); seasonal dummies; and the reform status variable.
The AFDC-UP entry rate equation regresses the entry rate (new UP cases divided by the population under age 49) on the gap between the employment rate and its previous maximum, seasonal dummies, and the reform status variable. The AFDC-UP exit equation regresses the exit rate (UP exits divided by the UP caseload) on the gap between the employment rate and its previous maximum, seasonal dummies, and the reform status variable.
D. POOLED CROSS-SECTION TIME-SERIES: STATE AGGREGATES
1. Introduction
In this section we describe previous efforts to model AFDC caseloads that used pooled state-level data for multiple states across states and over time. These models can be viewed as individual state time-series models that have been linked by using the same explanatory variables in all states and, with some exceptions, constraining the coefficients of each variable to be the same for all states. An important aspect of these models concerns the specification of the regression disturbance.
The general specification for this class of models is:
Equation 2.1: Yts = a+ b'Xts + ets
where:
Yts is the dependent variable for year "t" in state "s" (a measure of program participation);
Xts is a vector of explanatory variables;
a is the intercept;
b is a vector of coefficients for the explanatory variables (assumed constant across states and over time); and
ets is the regression disturbance.
There are various subclasses of pooled models, which are defined through the specification of the disturbance. For our purposes the most important subclass is "fixed effects" models. These models assume that the disturbance, ts, is the sum of three terms: a "state fixed effect" that is different for each state but doesn't vary over time; a "time fixed effect" that is different each year but doesn't vary across states; and a random effect. The subclass can be specified as:
Equation 2.2: Yts = b'Xts + as + tt + uts
where:
as is the state fixed effect;
tt is the time fixed effect for time period t; and
uts is the random disturbance.
We find it useful to think of the state fixed effect as the intercept term for the state; i.e., under this specification the regression intercept varies across states. This term will "explain," in a statistical sense, all of the cross-state variation in the average of the caseload variable overtime. Another way to state this is that it captures all factors that account for cross-state variation in the dependent variable that do not change over time.
Another way to interpret the fixed state effects specification is to recognize that it is equivalent to modeling the relationship between changes in the caseload variable to changes in the explanatory variables, with no state fixed effect (assuming appropriate specification of the other parts of the disturbance). The change model can be obtained by first differencing Equation 2.2:
Equation 2.3: DYts = b'DXts + Dtt + Duts
where the prefix D indicates the one period change in the variable. Because fixed state effects don't change over time, they drop out of the change specification. From this specification it is evident that we are ignoring the cross-section relationship between the levels of the variables in estimating the models' coefficients. Note that any X variables that vary only across states, and not over time, will drop out of the model, too.
The fixed time effects capture factors that change over time, but have an equal influence on the caseload variable in all states. One important example is the implementation of a new federal AFDC policy in all states at one time (example, OBRA81). To the extent that such a change has an equal impact on the participation variable in all states, its impact will be captured in the fixed time effects. The implementation of a new policy may be captured in fixed time effects over a number of periods because the impact may not be fully realized in the first period of implementation, or because it may be partly realized in anticipation of implementation. Unit impacts that are not uniform in all states will not be captured; unless captured by explanatory variables, they become part of the regression disturbance.
Fixed time effects are usually implemented by including a time dummy for each period, omitting the dummy for an arbitrarily chosen base period. These dummies "use up" all of the information that national time-series models would use to estimate the model, as is evident from the fact that a national time-series model with a dummy variable for each period could not be estimated. Assuming state fixed effects are also included, the coefficient estimates for the explanatory variables are based on the relationship between deviations of changes in the dependent variable from the national average change and deviations of changes in the explanatory variables from changes in their respective national averages. Thus, fixed effect results can be quite different than those obtained from national time series alone.
The other commonly used subclass of pooled models is known as "random effects" models. As in fixed effect models, the disturbance is usually assumed to have three components -- one that varies across states, one that varies across time periods, and a third that varies across both. The critical difference between random effects and fixed effects models is that the state and time components of the error term are assumed to be uncorrelated with the X variables in the former, but not in the latter. The uncorrelated assumption is built into estimators for random effects models. If the assumption is correct, the estimator will be more efficient than fixed effects estimators, but if it is incorrect the estimator may be biased, perhaps substantially so.
Fixed effects models are more commonly used for studying program participation at the state level than are random effects models. Fixed state effects are important because there are many time-invariant characteristics of states (e.g., geography) that could have an impact on participation and might well be correlated with explanatory variables. Fixed time effects may or may not be important, depending on whether significant national factors changed over the period under investigation, and whether those changes are associated with changes in the explanatory variables.
The two subclasses of pooled models may be mixed. The AFDC participation studies discussed below provide examples of models with fixed state effects, but not fixed time effects.
2. Previous AFDC Studies
Four studies have used pooled state data to analyze AFDC participation: Grossman (1985); Cromwell, Hurdle, and Wedig (1986); Moffitt (1986); and Shroder (1995). The first two of these use quarterly data, while the last two use annual data. In the discussion below we give more attention to the first two than the last two, for different reasons. As discussed previously, Grossman compares the findings from her analysis of pooled state data to results from a national time-series analysis. Cromwell et al. adopt an approach that is closer to the approach we recommend for this project than any other study.
Grossman (1985) estimates pooled Basic caseload and average Basic benefits models for states using specifications for each state that are very similar to the specifications she used for her corresponding national time-series models, described earlier. This is the earliest example of a pooled model that we have found. Quarterly data are pooled for 51 states (including DC) over the period from 1974.4 through 1983.4 (37 quarters) -- a total of 1,887 observations.
The caseload variable is the average monthly caseload during the quarter. Explanatory variables in the caseload equation include: a dummy for each state (i.e., a state effect); the national series for female headed households that was used in the national model, but allowing for a different coefficient for each state by interacting the variable with the state dummy; a single dummy for OBRA81, which permanently changes from zero to one in the quarter in which the state adopted a key requirement of OBRA81;(10) four lags of the number of persons unemployed; quarterly dummies; and the state's standard of need for a family of three.
Grossman concludes that her pooled caseload model performs very poorly relative to her national model, as well as relative to time-series models estimated for individual states. This conclusion is largely based on an R-square of only 52 percent, compared to an adjusted R-square of over 97 percent in the national time-series model and similarly high R-squares in the individual state time-series models. We find the low R-square to be very surprising. Our own experience in developing similar models for SSA disability program caseloads suggests that R-squares are typically very high because the state effects (i.e., individual state intercepts) explain all of the very considerable average cross-state variation in the dependent variable. Grossman's findings for the average benefit equation are more consistent with our experience; for that equation she obtains an R-square of 93 percent in the pooled model.
The low R-square in the caseload equation suggests that there is a significant specification problem. It may be that the low R-square is due to the following problem: the coefficient of the OBRA81 dummy is constrained to be the same in all states even though one would expect that the impact of the OBRA81 change on the level of the Basic caseload (i.e., on the dependent variable) would increase with the size of the state. There is tremendous variation in size across states, and one would expect comparable variation in the size of OBRA81's impact. The same criticism applies to the specification of the quarterly dummy variables and the standard of need.(11) There may be an analogous problem in the average benefit specification, but it is presumably much less severe because relative variation in average benefits across states is much smaller than relative variation in caseload size. The lesson from this experience is that state models should be specified in such a way that it is reasonable to expect coefficients to be constant across states. Later pooled models, discussed below, solve this problem by specifying logarithmic participation variables, so that each coefficient represents (approximately) the percentage change in participation associated with a unit change in the corresponding explanatory variable.
The Cromwell et al. (1986) study is unique among the studies we have examined because the focus of the study is Medicaid enrollment; AFDC participation is examined because most AFDC participants are Medicaid eligible. The authors measure AFDC participation as Medicaid enrollees who are also AFDC recipients; no distinction is made between Basic and UP households.(12)
The authors pool quarterly data from 44 states for the period from 1976 to 1982 (28 quarters and 44 x 28 = 1,232 observations). They implicitly use fixed state effects by specifying their model in quarterly changes. They do not specify fixed time effects, however.
The model's dependent variable is the natural log of average monthly AFDC Medicaid enrollment per capita for the quarter. All continuous explanatory variables are also in logs: the unemployment rate (current period plus three lags); monthly manufacturing earnings per capita; the maximum monthly AFDC payment level for a family of unspecified size, deflated; and a "tax capacity" index; a political "liberalism" index. In addition to these continuous variables, they include dummy variables for: whether or not a state has an UP program; whether or not the state has a Medicaid eligibility option for independent children between the ages of 19 and 21; and an OBRA81 dummy that is equal to one in the third quarter of 1981 and thereafter. They also include an interaction between the UP indicator and each of the unemployment variables. They hypothesize that participation will be more sensitive to business cycles in UP states than in non-UP states because the UP program is designed to help two-parent families when both parents are unemployed. Their findings provide strong support for this hypothesis.
The estimates of the impact of increases in the unemployment rate obtained by Cromwell et al. are several times larger than those obtained in the national time-series models we have reviewed. Their estimates imply that a one percentage point increase in the unemployment rate increases the caseload in states without an UP program by 1.8 percent after three quarters -- almost identical to CBO's estimate for Basic programs. IN states with an UP program, the estimated effect of the same change is a 3.0 percent increase after three quarters. Assuming that five percent of the caseload in the latter states is in the UP program, which is approximately correct, and that the sensitivity of the Basic program in those states is the same as in states with no UP program, the results imply that a one percentage point increase in the unemployment rate increases the UP caseload by 25.8 percent after three quarters -- more than 2.5 times the estimate obtained by CBO for the national UP caseload. One reason for the stronger result may be that the pooled methodology is better able to separate the effects of the recession in the early 1980s from the effects of OBRA81.
Moffitt (1986) uses the pooled state-level methodology to investigate whether there was a positive shift in AFDC participation among female-headed households from 1967 through 1982 that cannot be explained by labor market or programmatic changes, as many have alleged. Moffitt's analysis uses annual data for nine of the 16 years during the period of interest. The reason that seven years are excluded is that the participation variable in his model is estimated using data from the March Current Population Survey (CPS) and the biennial AFDC Characteristic Surveys (AS). Many states are excluded from the analysis because of missing data. The number of states included varies across years; the average number is just over 27; the total sample size (average number of states times years) is 245.
The dependent variable in Moffitt's model is the rate of AFDC participation among female-headed households; the numerator of the rate is based on AS tabulations and the denominator is based on CPS tabulations. Explanatory variables include the AFDC guarantee level, the benefit reduction rate (BRR), a dummy variable for southern states, the unemployment rate, and each of the following for female-headed households: mean age of head, mean education of head, percent of heads who are white, mean number of children, mean hourly wage rate, and mean unearned income.
Moffitt estimates equations for each year (i.e., using the cross-state data for the year alone), and also estimates three versions of pooled models: a model with fixed time effects but random state effects, a model with fixed time and state effects, and a "between" estimator.(13) The between estimator incorporates fixed time effects also, but ignores the possible existence of an error component that varies across states but not over time -- either random or fixed. It is obtained by jointly estimating cross-state regressions for each time period, constraining all coefficients to be the same except the intercept. As a result, the coefficients depend solely on cross-state relationships between the levels of the model's variables.
Moffitt's findings, taken alone, would be discouraging for those interested in examining AFDC participation through pooled analysis of state data. Very few of his explanatory variables, except the time dummies, are statistically significant using any of the three pooled estimators he considers, and those that are significant are not significant for all three estimators. The model with fixed state and time effects is especially disappointing, with no statistically significant coefficients other than for the fixed effects themselves. Further, the unemployment rate has an insignificant coefficient in all three specifications. The most significant findings are for the guarantee and BRR variables, in both the model with random state effects and the between model. The fact that these variables are not significant in the model with fixed state effects means that their significance in the other two models relies heavily on the cross-state relationship between these variables and participation, rather than on the relationships between changes in these variables and changes in participation over time. It is possible that the significant coefficients are substantially biased because important factors that both vary across states and are correlated with the explanatory variables, are not included in the equation.
There are many possible reasons why there are so few statistically significant coefficients in Moffitt's results, especially when compared to the findings of Grossman and Cromwell et al. The use of biannual data and the relatively limited number of observations are obvious ones. Moffitt also documents a number of problems with the construction of the dependent variable, as well as with some explanatory variables. Note, too, that Moffitt controls for a key demographic variable -- the number of female-headed households -- by using it as the denominator for the dependent variable. Hence, his estimates implicitly control for the effect that any of the explanatory variables would have on AFDC participation via their effect on the number of such households.
Of course one reason the estimates are insignificant may be that the explanatory variables are not very important determinants of participation. Moffitt explores this further with analysis of individual data for three of the seven years, and does find more significant effects. Nonetheless, these estimates, like the estimates using state-level data, imply that most of the increase in AFDC participation rates for female-headed households during the 1967-82 period was due to factors not accounted for by the models.
Shroder (1995) estimates a pooled state model using annual data from 1982 to 1988 for all 50 states and the District of Columbia (357 observations). His research focuses on the issue of endogeneity of AFDC benefits in participation equations. Specifically, he investigates the hypothesis that increases in AFDC participation reduce benefit levels because they increase the cost per taxpayer of each marginal dollar spent on benefits; as a larger share of the population participates in AFDC, there are fewer taxpayers per recipient to fund the program. For this reason he develops a two-equation model in which AFDC participation and benefits are jointly determined. Another unique feature of Shroder's model is the use of variables representing benefits and economic conditions in neighboring states.
The dependent variable in his participation equation is the log of the recipiency ratio (the ratio of AFDC recipients to non-recipients). The dependent variable in his AFDC benefit equation is the log of the maximum benefit for a 3-person household, including both the AFDC income guarantee and the value of Food Stamps.
Explanatory variables in the benefit equation include: the log of the recipiency ratio; an index of "Republican power;" the log of the share of AFDC recipients who are non-Hispanic whites; the log of the share of recipient households in which the mother of the youngest child is not married; the log of per capita disposable income; and the log of the state's share of AFDC benefit payments. Explanatory variables in the participation equation are (all in logs): the AFDC benefit variable, the average annual wages for laundry, cleaning and garment services (SIC 721), the unemployment rate, the ratio of women age 15-65 to employed men (F/EM; "it proxies for the availability of the marriage option"), a wage variable for the state's "composite neighbor" (see below), the composite neighbor's unemployment rate, F/EM for the composite neighbor, and the composite neighbors AFDC benefit.
Economic conditions and AFDC benefits in neighboring states are potentially important determinants of AFDC participation in one's own state because state residents may work in other states or migrate to other states to get work or obtain better AFDC benefits. The neighbor variables are weighted averages of variables in other states, with weights based on migration patterns from the 1980 census. Technically, the weight for state "k" as a neighbor for state "I" is defined as Wik = Mik/åkMik, where Mik is sum of migration from i to k and k to i.
Shroder uses instrumental variables for the benefit variable in the participation equation and the participation variable in the benefit equation to avoid simultaneity bias. He also estimates each model in two ways. In the first, he specifies fixed state effects (but not time effects), and in the second he averages the state data over seven sample years and estimate a cross-section model using the average state data. As discussed previously, the explanatory variable coefficients from the first estimator are based on the cross-state relationship between changes in the variables, and do not depend on the cross-state relationship between the levels of the variables. The second estimator is the antithesis of the first, relying on just the cross-state relationships in the average levels. Shroder's rationale for considering these estimators is worth examining:
"The fixed-effects model is particularly appealing in analyzing the recipiency ratio. Welfare recipiency across states may be affected by differential rates of divorce, abortion, teen pregnancy, size and social isolation of minorities, level of stigma attached to recipiency, structure of the economy, school quality, and so on. Many factors are difficult to measure well; the inclusion or exclusion of numerous imperfect measures will be controversial.
Assume these factors are time-invariant characteristics of the state. With the fixed-effects model, the choice problem of the representative agent can be conceived in terms of variables that do change over time, like the AFDC benefit paid in that state or in a neighboring state, and independent of the invariant factors.
However, two problems may arise with the fixed-effects model. First, the response to a change in the explanatory variables might occur with a lag of some unknown form. Second, the change in the explanatory variables from one period to another may consist of two shocks, one permanent and one transitory; the agents may be able to distinguish between them even if the econometrician cannot, and may respond only to the permanent component. In either case, the fixed-effects estimator will then be biased toward zero (Griliches and Hausman, 1986)." (Shroder, 1995, p. 186)
He goes on to argue that the estimator based on state averages, although possibly biased due to fixed effects, will mitigate problems arising from delayed responses and permanent versus transitory "shocks."
We concur with Shroder's rationale for using state fixed effects. The rationale for the state average estimator deserves closer examination. First, although the state-average estimator is likely to mitigate problems associated with delayed responses, another way to accomplish this and still include fixed state effects is to include lagged explanatory variables. In modeling SSA disability program participation using annual data, we have successfully used lags of as long as three years for unemployment with as few as seven years of data. The lagged variable strategy is likely to be even more successful with quarterly data, as the results reported by Cromwell et al. seem to indicate.
Second, use of lagged values will also help mitigate the problem of permanent versus transitory shocks to the extent that "agent" expectations are based on past experience rather than on other information that might portend a different future.
There is a third problem that Shroder does not mention, but which is mathematically identical to the permanent versus transitory shock problem: measurement error associated with the explanatory variables. As is well known to econometricians, random measurement error on an explanatory variable generally biases the variable's coefficient toward zero (i.e., the estimate understates the magnitude of the true coefficient), and the size of the bias is positively related to the share of the variation in the variable that is due to measurement error. Measurement errors in state average data tend to cancel each other out, implying that the share of variation in state averages for a variable that is due to measurement error is lower than the corresponding share for levels of the same variable in any given year. When year-to-year changes in a variable are examined, however, the share of variation due to random measurement error is higher than the share for the level of the same variable in a given year because some permanent variation across states has been removed and the variance of the random change in the measurement error is twice as large as the variance of the measurement error itself.
While we concur that the problems of delayed behavioral responses and permanent versus transitory shocks (including the measurement error problem) are problematic for the fixed state effects estimator and are mitigated by the state average estimator, it is preferable to deal with these problems as directly as can be done in the context of the fixed state effects estimator (e.g., by using lagged explanatory variables) than to resort to the state average estimator. Even though the latter mitigates these problems, it does so at the expense of accepting bias due to the state fixed effects. There are compelling reasons to believe that state fixed effects are important, and it seems likely that the bias resulting from ignoring them would be very large.
Based on Shroder's fixed effects estimates, the relationship between the recipiency ratio and the level of AFDC benefits is dominated by the effect of the former on the latter, although a significant reverse effect is identified. The fixed effect estimate of the coefficient of the benefit variable in the recipiency equation is both significant and large; a 10 percent increase in the benefit measure is associated with an increase in participation of almost 17 percent. The fixed effect estimate of the recipiency ratio coefficient is negative and significant, but not very large; a 10 percent increase in the recipiency ratio is associated with just a one percent reduction in benefits.
The fixed effects estimates of the own wage and unemployment coefficients in the participation equation are both statistically significant. A 10 percent increase in the benefit is associated with a 17 percent increase in the recipiency ratio, while a one percentage point increase in the unemployment rate is associated with a 3.5 percent increase in the ratio. Although his dependent variable differs from those used by CBO and Cromwell, his estimated effect is of the same magnitude for states with combined programs.
Only one of the four neighbor variables in Shroder's model has a statistically significant coefficient in the fixed effect estimates of the participation equation: a 10 percent increase in the neighbor wage index is associated with a 10 percent decline in the recipiency ratio. The neighbor AFDC benefit, unemployment and marriage variables are not statistically significant.
The state average estimates differ in many ways from the fixed effects estimates, indicating that the two sets of relationships captured by the two estimators are quite different from one another. Hence, it is important to recognize that these two sets of relationships are not the same.
3. Strengths and Weaknesses of the Pooled Approach
Strengths of the pooled approach include the following:
- For a given time period and data periodicity there are up to 51 times as many observations as in the national time series or the time series for a single state. This helps solve the multicollinearity problems that are common to national time-series models and allows for a richer specification of the model. Subject to availability, more variables can be included in the model;
- As with national or individual state time-series data, the dynamic impacts of explanatory variables can be explored, and the relatively large number of observations allows for richer dynamic specifications than are possible with a single time series;
- In comparison to national or state time-series estimates, it is feasible to control for all changes in national program policy or other national factors, at least to the extent that they have the same effects on participation in all states, by using time fixed effects. In the time-series approach, sample-size restrictions severely limit the number of dummy variables that can be used to estimate the effects of such changes without obscuring the effects of other variables;
- In comparison to national time-series analysis, the prospects for obtaining strong estimates of the impacts of program variables are much better because there is much more variation in individual state program variables than in weighted national averages of these variables. This applies to AFDC and other state programs, such as Medicaid and general assistance. The studies discussed above provide examples of multiple AFDC program variables used in the same model (Moffitt (1986) uses a maximum benefit variable and the earned income reduction rate, and Cromwell et al. (1986) use a maximum benefit variable and an UP dummy);
- The pooled methodology creates opportunities to test the validity of the model that are not possible with individual time series. Perhaps most importantly, we can test a set of constraints that is implied by the methodology itself -- identical coefficients for every state. Failure to reject the constraints would bolster confidence in the validity of the model. We could also test whether some or all coefficients are the same across two sample subperiods -- something which is difficult with a single time series because of limited observations. It is also possible to learn from comparing findings for various pooled specifications (e.g., fixed effects versus random effects), and to test whether the coefficients based on, say, cross-section relationships in the levels are the same as those based on cross-section relationships in changes of the variables.
The pooled methodology does have its limitations, however:
- It is methodologically more complex than the national time-series approach, which makes it more difficult both to implement and to describe the findings.
- Cross-state relationships between participation measures and explanatory variables in the model may in part reflect substantial cross-state variation in variables that have not been included, thereby biasing estimated coefficients for the included variables. State fixed-effects may need to be used to control for such factors;
- Collecting state level data requires more effort than collecting national level data. Data for some variables may not be available and the quality of other data may be poor. Data quality is particularly problematic when state fixed effects are used because measurement error bias is exacerbated by the use of the fixed effects;
- The estimated model is likely to track the participation measure for each state less well than a state time-series model, and the sum of the simulated series (i.e., across states) may track the national series less well than a simulation from a national time-series model. The reason for this is that the pooled methodology constrains explanatory variable coefficients to be the same in all states. If the constraints are valid, however, the pooled methodology should perform relatively well.
E. CROSS-SECTIONAL AND PANEL STUDIES OF MICRO DATA
Numerous studies have examined issues related to AFDC participation using cross-sectional data on individuals, usually obtained from large national surveys such as the Survey of Income and Program Participation (SIPP), the Panel Survey of Income Dynamics (PSID), and the Current Population Survey (CPS). The focus of many of the early studies has been the impact of AFDC benefit levels and the benefit reduction rate on the labor supply of female heads of households. These studies rely on the cross-state variation in AFDC benefits to estimate the impact on labor supply and find that the AFDC program does generate work disincentives; however, the magnitudes of the effects vary considerably across studies. For example, a review by Danziger et al. (1981) found the reduction in work effort to range from one to ten hours per week (10 to 50 percent of non-transfer labor supply levels).
Other studies have involved static models of AFDC participation, that is, the researchers estimate the likelihood of AFDC participation at a point in time as a function of demographic, economic, and AFDC program variables. These studies also find that the level of AFDC benefits and the benefit reduction rate significantly affect AFDC participation. The impact of wages on participation is also found to be important in some studies. Other factors significantly and positively associated with participation include age, having less education, poor health, and having greater numbers of children.(14)
Recent cross-sectional studies of AFDC participation have examined the importance of Medicaid, private health insurance, and medical need on AFDC participation (Blank, 1988; Moffitt and Wolfe, 1992). The findings from these studies have been mixed, mainly due to the manner in which the Medicaid benefit variable is specified. When the Medicaid variable (the value of Medicaid benefits) is specified at the individual level, based on the individual family's health status and medical care utilization, the results indicate that Medicaid availability has a significant positive effect on AFDC program participation. When a cruder measure of the value of Medicaid benefits is used, specified using a state-level average cost estimate, the relationship between Medicaid availability and AFDC participation is not significant.
Other recent literature on AFDC program participation has focused on the estimation of dynamic models of welfare participation using panel data on individuals, typically from the PSID or the National Longitudinal Survey of Youth (NLSY). These studies examine the determinants of program entry and exit, and time spent on the AFDC rolls. Using data from the PSID, Bane and Ellwood (1994) find race, education, marital status, work experience, and disability status to be important determinants of first-spell duration and recidivism. In examining the reasons for the first-spell of AFDC receipt, Bane and Ellwood find that changes in family structure account for about 80 percent of first-spells: over 40 percent begin when a wife becomes a female head, and 39 percent begin when an unmarried woman without a child becomes a female head with child. Only 7 percent begin due to a fall in the female head's own earnings, and about 5 percent due to a fall in other sources of income. The study does not address the factors that influence family structure. While their findings suggest that economic factors are unimportant, the effect of economic factors on family structure is not considered.
In studying welfare exits, Bane and Ellwood found that only about 25 percent of exits are due to an increase in the female head's earnings, while about 30 percent are due to marriage. The low rate of exits due to earnings in the Bane and Ellwood study is partially due to their hierarchical classification scheme that attributes an exit to marriage rather than earnings if the woman both married and increased her earnings. Other studies have found the proportion of welfare exits due to increased earnings to be in the range of 30 to 50 percent (Blank, 1988; Gritz and McCurdy, 1991; Pavetti, 1993). When Bane and Ellwood examine earnings in the first year off welfare regardless of marital status, they find that 41 percent of former recipients earned over $6,000 (1992 dollars) in that year.
Not surprisingly, the factors found to be associated with welfare exits differ between exits due to earnings and exits due to marriage or other factors. Greater education and previous work experience significantly increase the likelihood of earnings exits, but are not strongly associated with other types of exits. Race and marital status (never married versus widowed or divorced) have a much stronger influence on exits due to other reasons than on earnings exits. Never-married women and blacks are significantly less likely to leave welfare for marriage or other reasons (Bane and Ellwood, 1994).
The cross-sectional and panel studies of the determinants of AFDC participation provide important information about specific factors found to affect the likelihood of welfare entries and exits, and the duration of time spent on the rolls. The dynamic studies of welfare participation indicate that changes in family structure play a more important role than changes in a female head's earnings. This suggests that the direct effect of changes in the economy (i.e., the effect on the female head's earnings) on AFDC caseloads may be minimal. What one cannot determine from these studies is the indirect effect of changes in the economy on the AFDC caseload, as it impacts and causes changes in family structure. If poor labor market conditions for males affect the probability of marriage and/or divorce, then AFDC participation among females is also likely to be affected.
Fitzgerald (1991) touches on this issue in his study of determinants of AFDC exits by including a variable representing the quality of the "marriage market", that is, the ratio of single employed males to single males. This variable has a significant positive effect on the likelihood of welfare exits. His estimates indicates that a ten percent increase in the ratio of single employed males to single males decreases the likelihood of being on AFDC after 24 months by 8 percent (from 0.50 to 0.46).(15) In models where the effects were estimated separately for blacks and whites, however, the availability of single employed males had a significant positive effect on exits for whites only (a 10 percent increase reduces the likelihood of AFDC participation from 0.46 to 0.35 at 24 months). Another interesting finding from this study is that the unemployment rate had a significant negative effect on exits for blacks but was insignificant for whites. Taken together, these results indicate that the marriage market is more important for whites, and the labor market is more important for blacks in contributing to welfare exits.
While cross-sectional and panel studies are useful in identifying the important determinants of AFDC participation, they are much less useful in estimating the impacts of specific factors on caseload growth over time. The primary reason is that the marginal effects estimated in a cross-section (which rely on the variation across individuals at a point in time) are likely to differ from those estimated using aggregate changes over time. This is partly because the relationships among factors may change over time, and partly because the idiosyncratic behavior of individuals may introduce sufficient "noise" in the data to mask the effects of aggregate variables, unless very large sample sizes are available.
A few panel studies have a feature that makes them especially useful for examining the impact of labor market conditions and other area factors on AFDC participation of individuals. These studies link area labor market and other variables to individual observations, permitting the researcher to examine the relationship over time between changes in participation and changes in the area variables. Some studies have used major longitudinal survey databases and state-level area variables, but have found little evidence that changes in these variables have an impact on participation measures.(16) There are several possible reasons for the lack of findings, in addition to the possibility of no real effects. First, the number of observations in these surveys is small given the level of idiosyncratic variation in participation measures. Second, the studies typically control for demographic variables such as marital status, so don't recognize the potential impacts of area variables on household structure. Third, it may be that area variables for smaller areas than states are more relevant to participation than state variables, and changes in the variables for smaller areas may not be highly correlated with state-level changes.
Hoynes (1995) is the only study we know of to estimate a panel model of AFDC participation with area factors that uses a very large micro database and sub-state area variables. Her data were constructed from administrative records for AFDC recipients who are California Medicaid (Medi-Cal) enrollees -- nearly all AFDC recipients in the state -- for the period from 1987 to 1992. She estimates models for duration on AFDC using data for households that entered AFDC during the period. Her explanatory variables include household demographic variables, several county labor market variables, and community (Census tract or zip code area) demographic and economic variables based on the 1990 Census.
Hoynes found that the county market variables had substantial, statistically significant effects on duration in a variety of specifications. Her estimates imply that a three percentage point increase in the unemployment rate -- comparable to the average state-wide increase observed in California during the 1990-91 recession -- increases the chance that AFDC household that has been on the roles for less than 6 months will continue on the roles for at least one more month by 10 percent. Smaller effects were found for longer stayers. Similar results were found for other labor market variables. The findings are especially strong given that Hoynes controls for household characteristics that could themselves be influenced by labor market conditions.
F. POOLED CROSS-SECTION TIME SERIES: MICRO DATA
Several studies have used cross-sectional data on individuals, pooled over a number of years, to estimate the impact of various factors on AFDC participation. This approach offers the advantage of being able to capture the effects of and control for detailed demographic characteristics of the household while also estimating the impact of changes in state-level factors such as programmatic and labor market variables. Thus, for instance, the researcher might specify a binary choice (logit, probit, or linear probability) model for AFDC participation of families, using some explanatory variables that are specific to the family and others that are specific to the family's state, which may vary over time, but not across families within a state and time period (e.g., the state's unemployment rate).
Another advantage of the approach is that it can use variation in variables across families within a state and time period to estimate coefficients for variables that vary across families within each state and time period -- variation that is lost when state aggregate data are used. In fact, the researcher can use or not use a variety of sources of variation in the data, depending on how the model is specified. Just as in pooled analysis of aggregate data, the researcher can include dummy variables for each state to capture and control for all effects of factors that vary across states but not over time or across individual's within a state. Symmetrically, time dummies can be included to capture and control for all effects of factors that vary over time, but not across states. In addition, state and time dummies can be interacted to capture and control for all factors that vary both across states and over time, but not across families within a state and time period. When this is done, coefficients of other explanatory variables reflect only variation and covariation of variables across families within both time periods and states -- i.e., all of the variation that is lost when state aggregate data are used. As with the pooled analysis of state data, results will depend on which specification is used and differences in findings across various specifications may provide information that is useful in interpreting the results.
Yelowitz (1993) pooled individual-level data from the CPS for the years 1989 to 1992 to estimate the impact of Medicaid availability on the labor force and AFDC participation of single mothers. He tests the hypothesis that Medicaid expansions for children mandated by OBRA89 and OBRA90, that severed the link between AFDC and Medicaid eligibility for some groups, had the effect of reducing AFDC participation and increasing labor force participation. This is because the expansions allowed single mothers, in some cases, to earn more and still retain Medicaid benefits.
The Medicaid eligibility changes made it possible to study the effects of Medicaid coverage on AFDC and labor force participation in a number of ways: analysis of within-state variation based on the age of children (mothers with children of different ages either were or were not subject to the new expansions); analysis within states over time, as the expansions occurred; and analysis across states and/or time, as states adopted the optional expansions. Yelowitz estimates a probit model in which the Medicaid expansions are captured in a single variable, "GAIN%," which represents the increase in the Medicaid need standard as a result of the eligibility expansion, measured as a percent of the family's poverty line. The value of this variable for a family depends on both the family's state of residence and the age of the family's children.
While Yelowitz controls for individual demographic characteristics such as age, education, marital status, and the age of children in the family, he does not include any state-specific economic variables, such as the average wage or unemployment rate, in his analysis. He assumes the effect of these factors are captured by his state, time, and state-time interaction variables. This assumption is clearly correct when state-time interactions are included, because they control for all factors that don't vary across individual's within a state and time period. Evidence from previous analyses of pooled state data suggest that the assumption is incorrect when the state-time interactions are not included.
Yelowitz finds that Medicaid coverage independent of AFDC eligibility has a significant effect on both AFDC and labor force participation. Using the models with both state dummies and state-time interactions, he estimates that increasing the Medicaid need standard by 25 percent of the poverty line decreases the proportion of single mothers between the ages of 18 and 55 who receive AFDC by 4.6 percent, and increases their labor force participation rate by 3.3 percent. Estimated AFDC participation effects are somewhat smaller when state dummies and time dummies alone are used, with no interactions, suggesting that smaller effects would have been found if he had used aggregate data alone. This finding may have changed, however, had he controlled for the unemployment rate and other state-level factors. While variation in the Medicaid variable across families within states and time periods clearly made a substantial contribution to the strength of Yelowitz' Medicaid findings, the fact that the findings are still significant when state-time interactions are omitted provides some reason for optimism that Medicaid eligibility expansion effects can be identified using aggregate level data.
Gabe (1992) uses data from the March 1988 and March 1992 CPS to examine the effect of demographic changes on AFDC participation over the 1987 to 1991 period; intermediate year data are ignored. Gabe's analysis decomposes the recent growth in the AFDC caseload into growth due to change in the number and type of mother-only families and that due to change in the rate of AFDC recipiency. Gabe examines the growth in AFDC participation within subsamples of mother-only families with specific marital status and living arrangement characteristics. This is equivalent to controlling for those characteristics by estimating a linear probability model of AFDC recipiency using dummy variables for all possible marital status/living arrangement combinations as explanatory variables.(17)
Gabe attributes most of the caseload growth over the period to the growing number and changing composition of mother-only families, rather than to a change in the rate at which mother-only families receive AFDC. Changes in living arrangements contribute little to the growth experienced over the period, while changes in the number of mother-only families by marital status account for a substantial share (93 percent) of the growth in the AFDC caseload between 1987 and 1991.
Gabe's analysis does not take into account economic factors and their potential effect both on the rate of AFDC recipiency within the various marital status/living arrangement subgroups, and the share of the total population within each subgroup. His results indicate, however, that the effect of economic factors on recipiency rates would have to be strong in order to account for much of the growth up to 1991. They do not provide any indication of the extent to which changes in marital status and living arrangements can be attributed to economic factors.
A case could be made for developing a pooled cross-section time series model with individual data rather than a state aggregate model. For instance, a probit model for family AFDC participation could be estimated, limiting observations to those families with children. Separate models for single and two parent households could be developed. If duration data exist, duration could also be modeled. The explanatory variables would be a combination of household demographic variables, state economic variables, and variables that combine state program and household demographics (e.g., the AFDC payment for a household with the demographic characteristics of the observation; the value of Medicaid benefit for average household of same size). We might, for instance, build a SIPP database for this.
As discussed previously, this approach has the advantage of being able to control for household demographic characteristics while estimating the impact of aggregate changes over time. This approach does, however, have a number of important limitations:
- It would require considerably more resources to develop than would a state-level model, and would not span as long a time period, particularly if SIPP data were used;
- The demographic variables that this approach allows us to include are mostly ones that may themselves be influenced by the economic factors we are considering. In fact, the existence of the family itself -- the basic unit of analysis -- may, in part, be determined by economic factors. Gabe's failure to find evidence of the impact of economic factors may be due this problem;
- Individual-level survey data are often annual in nature, and therefore would not capture important dynamics associated with AFDC participation; and
As with cross-sectional studies of individual data, the idiosyncratic behavior of individuals may obscure the effects of aggregate variables in the analysis unless sample sizes are extraordinarily large.
G. PARTICIPATION MEASURES
In this section we describe the measures of AFDC participation that have been used in previous studies of caseload growth and discuss issues relevant to the choice of a dependent variable for our analysis.
The most common measure of AFDC participation used in previous studies of caseload growth is the number of AFDC Basic or UP cases, typically measured as the number of families receiving benefits in a given month, or the average number of families for a given quarter or year (Exhibit 2.1). Quarterly data are used in the national studies of caseload growth, while the use of monthly data is more common among the individual state forecasting models. The pooled studies of state date use either quarterly or annual data.
Models that use case openings and closings for the dependent variables are rare. The state of Washington uses entries and exits to forecast its AFDC-Basic and UP caseloads in separate models. CBO includes an analysis of case openings and closing (Basic and UP cases combined) in the appendix to their main caseload analysis (CBO, 1993). The CBO study cites inconsistencies in administrative reporting of openings and closings as a major problem in using these data to analyze caseload growth. By comparing the estimated caseload, computed using changes in openings and closings, to the actual caseload, they illustrate how the estimated and actual series diverge due to the reporting problems associated with case openings and closings.
According to the CBO report, the problem arises because only families who enter the caseload through the formal application process are counted as case openings. Families who were on AFDC and return after a short period off the program are often not required to file a formal application. For these families, a closing would have been initially reported, but the subsequent opening would not be counted. It is also frequently the case that, for families who go on and off the rolls during a short period, neither the subsequent openings nor closings are documented.(18) This poses a major problem in using openings and closings to analyze the dynamics of caseload growth, as a portion of the caseload that is in transition will be lost to the analysis. This is especially unfortunate because those moving on and off the rolls during shorter periods are likely to be most affected by changes in the economic factors that determine AFDC participation.
Another important measure used as the dependent variable in a few models is AFDC expenditures or average payments. A primary reason for analyzing caseload growth is to determine the implications of changing factors on federal and state AFDC expenditures. Using expenditures or average payments as the dependent variable allows the effects of economic, demographic, and programmatic factors on AFDC expenditures to be estimated directly, rather than inferred from analyses that model caseloads. It is possible that expenditures are more sensitive to changes in the economy than are caseloads. They may be more sensitive if economic downturns not only induce additional individuals to apply for benefits, but also cause those already on the rolls to experience a fall in earned income and a corresponding increase in AFDC benefits. This effect may be negated, however, if those coming on the rolls receive lower than average benefits.
Exhibit 2.1
Measures of AFDC Participation used as Dependent Variables in Previous Studies
| Variable | Type | Description | Model(s) |
|---|---|---|---|
| AFDC-Basic
Caseload |
Quarterly, national | Grossman (1985);
CBO (1993) |
|
| Quarterly, state | Barnow (1988) | ||
| Quarterly, state | Seasonally adjusted | Florida | |
| Quarterly, state | Average number of cases receiving benefits in that quarter | Garasky (1990) | |
| Monthly, state | Texas; Oregon; Minnesota; Maryland | ||
| AFDC-UP Caseload | Quarterly, national | Grossman (1985);
CBO (1993) |
|
| Quarterly, state | Barnow (1988) | ||
| Monthly, state | Minnesota; Maryland | ||
| AFDC Entries (Openings) | Quarterly, national | AFDC-Basic and UP openings combined | CBO (1993) |
| Monthly, state | Separate data series for Basic and UP entries | Washington | |
| AFDC Exits
(Closings) |
Quarterly, national | AFDC-Basic and UP closings combined | CBO (1993) |
| Monthly, state | Separate data series for Basic and UP exits | Washington | |
| AFDC Cash Medicaid Enrollees per Capita | Quarterly, state | Cromwell et al. (1986) | |
| AFDC-Basic Expenditures | Quarterly, state | Florida | |
| Recipiency Ratio | Annual, state | Log of ratio of AFDC recipient population to non-AFDC recipient population | Shroder (1995), recipiency model |
| AFDC Participation Rate of Female Household Heads | Annual, state | AFDC participation rates of female household heads derived from the CPS. | Moffitt (1986) |
| Average Benefit per Household, AFDC-Basic | Quarterly, national | Grossman (1985) | |
| Quarterly, state | Grossman (1985) | ||
| Average Benefit per Household, AFDC-UP | Quarterly, national | Grossman (1985) | |
| Quarterly, state |
H. EXPLANATORY VARIABLES
In this section we describe the main explanatory variables that have been used in previous studies. We focus on the variables included in time-series and pooled models using aggregate data, which are the most relevant for the purposes of this project. We organize the section by the different types of variables -- demographic, economic, AFDC program, and other programs and laws.
1. Demographic Factors
All the models of AFDC caseload growth we reviewed include a number of demographic explanatory variables, the most common being the size of the population of female-headed households; however, a number of studies have simply used total population or total female population measures. Other commonly used variables are births (out-of-wedlock, in-wedlock, or fertility rates), and the number of divorces (Exhibit 2.2).
Several issues arise in considering which demographic variables to include in a model of AFDC caseload growth. First, should overall population measures be used or population measures that also incorporate family structure (e.g., total female population ages 15 to 45 versus the number of female-headed households)? Because economic factors are likely to determine family structure and therefore, their importance may be understated in models that use family structure as an explanatory variable.
Second, there is an issue surrounding the changing age distribution of the female population. As the population ages, presumably the propensity to participate in the AFDC program among female-headed households also changes. None of the studies we reviewed addressed the changing age distribution of the population or the potential impact on AFDC caseloads.
Third, there is the issue of stock versus flow measures when using births, marriages, or divorces as explanatory variables. Births, marriages, and divorces all are flow variables that each have marginal impacts on the size of the population at risk for AFDC participation (single mothers). Such variables would be appropriate for models that focus on openings and closings because these, too, are flow variables, but are inappropriate for modeling the size of the caseload directly. For the latter, explanatory variables reflecting the stock of individuals at risk for AFDC participation seem more appropriate.
Fourth, while detailed family structure data are available from surveys at the national level, they are not generally available at the state level. One pooled model (Grossman, 1985) used a national series for female-headed households in the equation for each state, allowing the coefficient to vary across states. Two state models, for Maryland and Texas, use monthly state female-headed household series. In the case of Maryland, however this series is interpolated between Census observations. We have not received information on how the series for Texas was constructed, but note that Texas is large enough so that estimates based on the Current Population Survey would be reasonably accurate.
Exhibit 2.2
Demographic Variables used in Previous Analyses of AFDC Caseload Growth
| Variable | Type | Description | Model(s) |
|---|---|---|---|
| State Population | Quarterly, state | Total state population; quarterly data interpolated from annual data | Cromwell et al. (1986); Barnow (1988) |
| Quarterly, state | State Population, ages 15-44 | Garasky (1990) | |
| Female Population | Quarterly, state | Female Population, ages 15-45 | Florida |
| Monthly, state | Female Population, ages 15-44 | Oregon, AFDC-Basic model | |
| Female Headed Households | Quarterly, national | Number of families headed by women with own children under 18 multiplied by ratio of never married mothers to mothers who have been married | CBO(July 1993), AFDC-Basic model |
| Quarterly, national | Number of female headed households | Grossman(1985), AFDC-Basic model. | |
| Monthly, state | Number of never-married female headed households with children under 18 | Texas | |
| Monthly,
state |
Number of separated/divorced female headed households with children under 18 | Texas | |
| Monthly, state | Number of female headed households with children under age 18; data interpolated from 1980 and 1990 data using the Maryland Demographic Model | Maryland, Balance of state AFDC-Basic model | |
| Unmarried mothers | Annual, state | Log of proportion of recipient households for whom the mother of the youngest child is not married | Shroder (1995), benefit model only. |
| Births | Quarterly, state | Sum of out-of-wedlock births over previous two years | Barnow (1988) |
| Quarterly, state | Number of live births to all mothers aged 15 through 19 (lagged one quarter) | Garasky (1990) | |
| Monthly, state | Fertility rate of unwed women, ages 15-44 | Oregon, AFDC-Basic model | |
| Monthly, state | Number of births | Oregon, AFDC-Basic model | |
| Monthly, state | Number of out-of-wedlock births | Minnesota (AFDC-Basic Model) | |
| Monthly, state | Number of in-wedlock births | Minnesota (AFDC-UP Model) | |
| Monthly, state | Out-of-wedlock birth rate | Washington, AFDC-Basic entry equation | |
| Number of Children under Age 18 | Annual, individual | Number of children under Age 18 of female household heads | Moffitt (1986) |
| Divorces | Quarterly, state | Number of divorces | Barnow (1988) |
| Monthly, state | Number of divorces | Oregon, AFDC-Basic model | |
| Marital Status of Mother-Only Families | Annual, national | Decomposition into never married, separated/other, divorced, and widowed categories | Gabe(1992) |
| Living Arrangements of Mother-Only Families | Annual, national | Decomposition into independent families, extended families, cohabitation, and unrelated families categories | Gabe (1992) |
| Size of Labor Force in States with UP Programs | Quarterly, national | Grossman(1985), AFDC-UP model | |
| State's Own F/EM Ratio | Annual, state | Log of ratio of women age 15-65 to employed men in state | Shroder (1995), recipiency model. |
| State's "Composite Neighbor's" F/EM Ratio | Annual, state | Log of ratio of women age 15-65 to employed men in state's "composite neighbor" | Shroder (1995), recipiency model. |
| Anglo Recipients | Annual, state | Log of proportion of AFDC household heads who are non-Hispanic whites | Shroder (1995), benefit model. |
2. Labor Market and Economic Factors
Nearly all models of AFDC participation include measures of labor market conditions as explanatory variables (Exhibit 2.3). The most commonly used measure is the unemployment rate. Many models include both current and lagged values of the unemployment rate in their specifications. Other variables intended to capture labor market conditions that were used instead of the unemployment rate include: the number of unemployment insurance claims filed, employment rates of females or in female-dominated industries, and employment gap measures (the difference between current and full employment).
In addition to the unemployment rate, models frequently include a measure of earnings. These range from overall average earnings for females within a specified age/education group (males, in UP models), to average wages in specific industries. Wage data for the retail trade industry or for "predominantly female" industries were used in some Basic models, while manufacturing wages were used in some UP models as well as in one Basic model (Cromwell et al., 1986). Many researchers have found that both the unemployment rate, or some other employment measure, and an earnings variable have statistically significant coefficients -- experience that suggests there is room for both types of measures in our models.
Availability of accurate data at the state level and by quarter is a key issue. The unemployment rate is available at this level and is generally considered to be of high quality. It is our understanding that the Bureau of Labor Statistics (BLS) collects state-level earnings data by industry on a monthly basis, but does not tabulate it at the state level other than annually. The state-level monthly or quarterly earnings data used in some models evidently come from special tabulations of BLS data. We are investigating the feasibility of having BLS prepare special tabulations for this project.
Another issue related to the use of an earnings variable is whether or not earnings should be adjusted to reflect taxes. Only one model has used an after-tax measure of earnings, and in this case, it is used in combination with the AFDC benefit to construct a variable representing the net gain to participating in the AFDC program.(19) Federal tax adjustments, including potentially important Earned Income Tax Credits, can be made fairly simply based on a set of standard assumption about a family. State adjustments are probably not feasible because they vary by state.
A final issue concerns the inclusion of lagged values. CBO (1993) uses the longest lag specification on a labor market variable of any study reviewed -- six quarters in the UP equation only (three quarters in the Basic equation). No other specification uses a lag length of more than one year. Use of pooled data for states makes it feasible to explore longer lag lengths in comparison to what might be feasible using time-series for a single geographic area. This could be important because national time-series data suggest that economic recovery from a recession is followed by very slow declines in program participation. The pooled studies to date, however, have not considered longer lag lengths.
Exhibit 2.3
Economic Variables Used in Previous Studies of AFDC Caseload Growth
| Variable | Type | Description | Model(s) |
|---|---|---|---|
| Unemployment | Annual, state | State unemployment rate | Moffitt (1986) |
| Annual, state | Log of average unemployment rate in state | Shroder(1995), recipiency model | |
| Quarterly, national | Current and lagged unemployment rates | Grossman (1985) | |
| Quarterly, state | Three month average; seasonally adjusted and unadjusted rates | Barnow (1988) | |
| Quarterly, state | Seasonally adjusted unemployment rate | Florida | |
| Quarterly, state | The number of unemployed persons, three month average | Barnow (1988) | |
| Quarterly, state | Average number of weekly unemployment insurance claims measured in thousands of claims (current and lagged one and two quarters) | Garasky (1990) | |
| Monthly, state | New unemployment claims smoothed two months | Maryland, AFDC-UP model | |
| Monthly, state | Various lags of unemployment rate | Minnesota, Basic and UP models | |
| Employment | Annual, state | Proportion of female household heads employed full time | Moffitt (1986) |
| Annual,
state |
Proportion of female household heads employed part time | Moffitt (1986) | |
| Monthly, county | Ratio of aggregate level of employment in seventeen female dominated industries (females> 40% of workers) and the number of female headed households with related children | Maryland, Prince George's County AFDC-Basic model | |
| Employment Gap | Quarterly, national | Percent difference between potential and actual employment (current and lagged three quarters for Basic; current and lagged five quarters for UP) | CBO(1993), AFDC-Basic and AFDC-UP models |
| Monthly, state | Gap between "full" employment (5.5 percent unemployment) and actual non-agricultural employment | Texas | |
| Monthly, state | Gap between current employment rate and its previous maximum | Washington, Basic exit model, UP entry and exit models | |
| State's "Composite Neighbor's" Unemployment Rate | Annual, state | Log of average unemployment rate in state's "composite neighbor" | Shroder (1995), recipiency model |
| Product of UP Program Dummy and State's Unemployment Rate | Quarterly, state | Unemployment rate, current and lagged three quarters, for states with UP program | Cromwell et al. (1986) |
| Real Earnings of Women, HS, 18-24 | Quarterly, national | Average earnings of women aged 18 -24 with exactly four years of high school and who work full time, year round, in 1991 dollars | CBO (1993), AFDC-Basic |
Exhibit 2.3 (Continued)
Economic Variables Used in Previous Studies of AFDC Caseload Growth
| Variable | Type | Description | Model(s) |
| Real Earnings of Men, HS, 18-24 | Quarterly, national | Average earnings of men aged 18 -24 with exactly four years of high school and who work full time, year round, in 1991 dollars | CBO (1993), AFDC-UP |
| State's Own Wage Level | Annual, state | Log of average weekly wages for laundry, cleaning, and garment services in state (SIC 271) (nominal). Source: Employment and Wages Annual Averages, Bureau of Labor Statistics, 1982-1988. | Shroder (1995), recipiency model |
| Disposable Income | Annual, state | Log of per capita after tax income | Shroder (1995), benefit model |
| State's "Composite Neighbor's" Wage Level | Annual, state | Log of average annual wages for laundry, cleaning, and garment services in state's "composite neighbor" (SIC 271) (nominal) | Shroder (1995), recipiency model |
| Manufacturing Wage | Quarterly, state | Average monthly manufacturing earnings (real) | Cromwell et al. (1986) |
| Retail Wage | Quarterly, state | Average weekly wage in retail trade (real) | Barnow (1988), Garasky (1990) |
| Monthly, state | Average real wage rate in retail industry | Texas | |
| Retail/Wholesale Wage Index | Monthly, state | Calculated from total wage bill for selected retail and wholesale trade industries | Maryland, AFDC-UP model |
| Interaction Weekly Wage in Retail Trade Variable | Quarterly, state | OBRA dummy variable multiplied by average weekly wage in retail trade (real) | Barnow (1988) |
| Monthly Non-wage Income | Annual, individual | Sum of non-transfer non-wage income and earnings of others in 1977 dollars, divided by 100, for female household heads | Moffitt (1986) |
| Tax Capacity per Capita (in $1000s) | Quarterly, state | Measure reflects alternative forms of taxpayer revenues in addition to personal income, e.g., property and corporate taxes, severance taxes; Source: Advisory Commission on Intergovernmental Relations (1983) | Cromwell et al. (1986) |
| Poverty Level | Monthly, state | Federal poverty level income for a family of three | Oregon, AFDC-Basic model |
| Index of Help Wanted Advertisements | Monthly, state | Index of help wanted advertisements (lagged twelve months, smoothed two months in recovery model; lagged eight months, smoothed two months in recession model); Source: Regional Economic Studies Program, University of Baltimore | Maryland, Balance of state AFDC-Basic model, excludes Prince George's County |
| Monthly, metro area | Index of help wanted advertisements for District of Columbia metro area, lagged thirteen months, smoothed four months; Source: Regional Economic Studies Program, University of Baltimore | Maryland, Prince George's County AFDC-Basic model | |
| Seasonal Dummies | Quarterly | Grossman (1985); Cromwell et al. (1986); Barnow (1988); CBO (1993) | |
| Monthly Dummies | Monthly | Washington, AFDC-Basic and AFDC-UP entry and exit models |
3. AFDC Program Variables
Variables reflecting changes in AFDC benefit levels and the implementation of new policies that either affect eligibility or the conditions under which individuals may receive benefits are typically incorporated in models of AFDC caseload growth (Exhibit 2.4).
The AFDC benefit variable is expressed in a variety of ways. It is most commonly expressed as the real dollar value of the maximum benefits for a family of a given size, typically a three person household. In some studies, the value of Food Stamp benefits combined with the AFDC benefit is used instead of the AFDC benefit alone. The combined variable more accurately reflects the benefits to a household that participates in the AFDC program than the AFDC benefit alone because Food Stamp benefits are reduced by 30 cents for each additional dollar of income, including income from AFDC. As a result, Food Stamp benefits are relatively high in states with relatively low AFDC benefit levels. This leads to less variation across states when the combined benefit measure is used than when the AFDC benefit alone is used as the explanatory variable.
A few studies have used measures of AFDC benefit levels that express benefits relative to some measure of earnings, either as a ratio of benefits to earnings, or as the difference between after-tax earnings and AFDC benefits. Incorporating earnings and benefits in this manner imposes a restriction on the independent effects of earnings and benefits on participation. An alternative strategy is to specify the two variables separately and then test the implied restriction. We think this strategy is especially important in a study that seeks to identify causal relationships.
One study treats the AFDC benefit level as an endogenous variable, jointly determined with the rate of recipiency (Shroder, 1995). The logic is that welfare benefits are a public good and their provision is, in part, determined by the preferences of voters (taxpayers). In states with a high proportion of AFDC recipients, AFDC benefits will be lower because the cost of an additional dollar of benefits to taxpayers is higher. An instrumental variable is used for the AFDC benefit level in the recipiency model. This study finds a very large estimated effect for increases in the maximum monthly benefits -- about twice as large as when no instruments are used.
Variables reflecting changes in national AFDC policies over time are also included in a number of models. Examples of these are OBRA81, the Deficit Reduction Act of 1984, and the JOBS program in 1990. In many of the individual state models, variables reflecting state AFDC policy changes are also included. None of the national studies cover the most recent years when a variety of waivers have been granted to states to experiment with their AFDC programs, and therefore do not address these policy changes in their models. Such variables are included in some of the individual state models we reviewed.
Exhibit 2.4
AFDC Program Variables Used in Previous Studies of AFDC Caseload Growth
| Variable | Type | Description | Model(s) |
|---|---|---|---|
| AFDC State Share | Annual, State | Log of difference of one minus federal matching rate | Shroder (1995), benefit model |
| AFDC Benefit | Annual, state | Log of state's own maximum monthly AFDC grant to a three person household plus Food Stamp benefit dollar value | Shroder (1995), recipiency model |
| Annual, state | Dollar value of maximum monthly AFDC benefit for a family of four in 1977 dollars, divided by 100 | Moffitt (1986) | |
| Quarterly, national | Maximum AFDC Benefit for a family of three, expressed in 1991 dollars; weighted average of state benefits | CBO (1993) | |
| Quarterly, state | Real maximum AFDC payment level | Cromwell et al. (1986) | |
| Monthly, state | Real value of average annual AFDC cash grant to a family of three | Oregon | |
| Monthly, state | Combined real cash value of monthly AFDC, Food Stamp, and Medicaid benefits for the average three person AFDC family | Texas | |
| Net Gain Index | Monthly, state | Real difference between after tax earnings (Wages + EITC + Food Stamps - FICA) received by female workers in female dominated industries and benefits paid to a three person AFDC family (maximum monthly AFDC benefit + the maximum monthly Food Stamp grant + average monthly Medicare expenditure); values lagged 12 months in recovery model and 6 months in recession model | Maryland, Balance of state AFDC-Basic model, excludes Prince George's County |
| Grant-Earnings Ratio | Monthly, state | Ratio of three person grant to typical earnings in non-manufacturing employment | Washington, AFDC-Basic exit |
| AFDC-Basic Need Standard | Quarterly, state | Real AFDC-Basic need standard for a family of three taken at the midpoint of quarter | Garasky (1990) |
| State's "Composite Neighbor's" AFDC Benefit | Annual, state | Log of state's "composite neighbor's" maximum monthly AFDC grant to a three person household plus Food Stamp benefit dollar value | Shroder (1995), recipiency model |
| Benefit Reduction Rate | Annual, state | Percent reduction in benefits for each additional dollar of earnings | Moffitt (1986) |
| OBRA81 Immediate Effect | Quarterly, national | Dummy equals one in 1981.4 and zero in all other quarters | Grossman (1985); CBO (1993) |
| Quarterly, state | Dummy equal to one in 1981.4 and zero in all other quarters | Barnow (1988) | |
| OBRA81Phase-In Effect | Quarterly, national | Dummy equals one in 1982.1 and zero in all other quarters | Grossman (1985); CBO (1993) |
| Quarterly, state | Dummy equal to one in 1982.1 and zero in all other quarters | Barnow (1988) |
Exhibit 2.4 (Continued)
AFDC Program Variables Used in Previous Studies of AFDC Caseload Growth
| Variable | Type | Description | Model(s) |
|---|
| OBRA81 Permanent Effect | Quarterly, national | Dummy equals one in 1982.2 and all subsequent quarters. Dummy equals zero in all quarters before 1982.2 | Grossman (1985) |
| Quarterly, national | Dummy equals one in 1981.4 and all subsequent quarters. Dummy equals zero in all quarters before 1981.4 | CBO (1993) | |
| Quarterly, state | Dummy equal to one in quarter when state adopted OBRA81 standard of need rule and all subsequent quarters | Grossman (1985) | |
| Quarterly, state | Dummy equal to one in 1981.4 and all subsequent quarters | Barnow (1988) | |
| Quarterly, state | Dummy equal to one in 1981.3 through 1982 | Cromwell et al. (1986) | |
| AFDC Kids 18-21 Option Dummy | Quarterly, state | Dummy equal to one if state has AFDC Kids 18-21 option | Cromwell et al. (1986) |
| AFDC-UP Dummy | Quarterly, state | Dummy equal to one if state has an AFDC-UP program | Cromwell et al. (1986) |
| Deficit Reduction Act of 1984 | Quarterly, state | Dummy equal to one in 1984.1 and all subsequent quarters | Barnow (1988) |
| AFDC Policy Dummy | Quarterly, state | Dummy equal to one from 1987.4 to 1992.4 to represent various state policy changes | Florida (Legislative model) |
| JOBS Implementation Effect Dummy | Monthly, state | Dummy equal to one in 1990.4 | Texas |
| FIP or FSA Variable | Monthly, state | Percentage of state operating under Washington's Family Independence Program (1988) or federal Family Support Act (1990) | Washington, all models |
| Lagged AFDC-UP Caseload Index | Monthly, state | Lagged one month | Maryland, AFDC-UP model |
| AFDC-Basic Case Closure Rate | Monthly, state | Maryland, AFDC-Basic model | |
| Workfare Dummy | Monthly, state | Dummy representing the effect of a new workfare program providing transitional benefits | Kansas |
4. Other Variables
Other than demographic, economic, and AFDC program variables, there are few examples of additional explanatory variables used in studies of AFDC caseload growth (Exhibit 2.5). Two studies have used indicators of a state's political climate, and several of the individual state models include indicators for policy changes indirectly related to the AFDC program.
One potentially important factor, included in only one caseload model we reviewed, is the Medicaid eligibility expansions that took place during the late 1980s and early 1990s. These changes expanded eligibility for Medicaid beyond AFDC eligibility for certain groups, including pregnant women and young children. Yelowitz (1993) finds that the expansions had a significant negative impact on AFDC participation.
No studies we have examined have looked at the potential impacts of changes in SSI (including state supplements), Social Security Disability Insurance, general assistance, unemployment insurance, or any other program on participation in AFDC. Further, none have included variables for changes in laws concerning child support, abortion policy, or others that might have an impact on participation.
Exhibit 2.5
Other Variables Used in Previous Studies of AFDC Caseload Growth
| Variable | Type | Description | Model(s) |
|---|---|---|---|
| Republican Power | Annual, state | Log of weighted average of percent Republican vote for president and percent of house seats captured by Republicans; values interpolated between election years | Shroder (1995) |
| Liberalism Index | Quarterly, state | Based on liberal quotients produced by the Americans for Democratic Action in which each U.S. senator and congressperson is assigned a number between 0 to 100 based on their votes on twenty key issues each year; liberalism index averages quotients within each state and standardizes by the national average to avoid temporal bias | Cromwell et al. (1986) |
| Medical Assistance Expansion | Monthly, state | Dummy representing the expansion of medical assistance for pregnant women and their children | Kansas |
| MinnesotaCare | Monthly,
state |
Dummy representing implementation of a subsidized health insurance alternative to Medicaid. | Minnesota |
| Sex Education | Monthly, state | Dummy equal to one after 1974 when mandatory sex education in schools was initiated. | Alabama |
| Right to Work Bill, 1986 | Monthly, state | Dummy captures effect of 1986 Right to Work Bill | Tennessee |
I. CONCLUSIONS
In this section we discuss how our findings from the literature review have influenced how we have specified our models. We begin with a discussion of substantive issues concerning the specification of econometric models, then turn to a discussion of more technical specification issues.
1. Substantive Issues
Basic and UP Models
Although some previous researchers have examined the combination of Basic and UP participation, the predominant approach is to consider these programs separately. There are sound methodological reasons for considering them separately, especially given the fact that the UP program became mandatory in 1990, and because data for doing so are readily available -- although potential interactions between the programs should be recognized. Hence, we have developed separate participation models for these programs. It should be recognized, however, that cases in one program may shift, over time, into the other program. We have allowed for potential interactions in only a very simple way -- by including dummy variables for the presence and type (6-month or 12-month) of UP program in the Basic participation equations.
Household Demographic Variables
Past efforts have commonly used the number of female-headed households with children under the age of 18 or similar measures as explanatory variables, rather than more general population measures such as the size of the female or male population in a specific age group. There is reason to believe, however, that such variables themselves are sensitive to economic factors, and controlling for such variables may result in an understatement of the impact of changes in economic variables on AFDC participation. We examine this issue by estimating models with and without such variables included.
Age Distribution of the Population
We did not find any studies using aggregate data at either the national or state level that directly examined the impact of changes in the age distribution of the population on AFDC participation, although there is evidence from studies using individual data that participation varies with the age of the household head. During the time period we are examining, there was a substantial change in the age distribution of the population that is most at risk for AFDC -- those between 16 and 45 -- as the Post World War II "baby boom" generation completed its entrance into this age group earlier in the period and began to age out of the age group by the end of the period. In our previous work in modeling participation in the Social Security Administration's disability programs over the same period, we have taken this factor into account and found it to be important (Lewin-VHI, 1995b and 1995c).
Labor Market Variables
The specifications and findings in the literature we have reviewed suggest that the unemployment rate and some measure of average hourly earnings will be key explanatory variables and that the full impact of changes in these variables on AFDC participation will be realized only after four to six quarters have passed, especially for the unemployment rate. As discussed above, even longer lags may be important. State-level data for such variables are available although only at the annual level. Earnings adjustments to reflect federal taxes and earned income tax credits are feasible, although they have rarely been done in previous studies, and we have followed suit. Previous studies have not considered industry level measures of employment, but such measures may more accurately reflect the effects of business cycles on the segment of the labor market that is most relevant to potential AFDC recipients.
Measuring AFDC Benefits
Most studies use a maximum monthly benefit variable for a household of specified size, and some adjust this variable for Food Stamps. Failure to adjust for Food Stamps results in an overstatement of the effect of an increase in the benefit of the family's income. The AFDC benefit variable is sometimes combined with the earnings variable into a single variable, but we think this is a mistake if it is feasible to start with separate variables and test the restriction that combining the variables implies. One study that is methodologically similar to this study also uses a benefit reduction rate and obtains strong results (Moffitt, 1986). Hence, we were encouraged to develop a similar measure for this study.
Simultaneous Determination of AFDC Benefits
While most studies have assumed that the AFDC benefit variable is exogenous to participation, there are theoretical reasons and empirical evidence to support the hypothesis that increases in participation create down-ward fiscal and political pressure on the level of benefits. If so, the coefficient of the benefit variable may understate the effect of an increase in benefits on participation. Correction of this problem requires use of an instrumental variables technique, but it may be difficult to find the right instruments. This is complicated when more than one benefit variable is used, as in our models. While this issue may be an important one, we have neglected it here in favor of addressing other issues that seemed more important and easily dealt with.
Average Benefits per Case
We originally had planned to focus on participation in our analysis, ignoring the issue of average benefits per case. Some previous studies have, however, examined average benefits per case and found some evidence of sensitivity to economic factors -- even though average benefits are largely determined by maximum benefit levels. We decided to develop a model of average benefits per case in order to more fully understand the impacts of the business cycle and other economic factors on AFDC expenditures.
Other Programs
The literature we reviewed has not examined the impact of changes in other state programs on AFDC participation, with the exception of Medicaid. The findings from the Yelowitz (1993) study on Medicaid expansions encouraged us to think we would find a similar Medicaid impact. Based on our previous analysis of SSI participation, it seemed likely that impacts of changes in other programs on AFDC might be identified using the pooled state methodology.
2. Technical Issues
Pooled analysis of state data versus alternative methods
Based on our prior experiences and the findings of this review, we concluded that pooled analysis of state-level data shows greater promise than other approaches to studying the determinants of program participation. In comparison to time-series approaches for the nation as a whole, this approach allows examination of state-level programmatic changes, provides a much richer way to study the impact of other factors that vary at the state level, and provides many more opportunities for testing the validity of the model. Individual state time-series models offer some of these advantages, but don't take advantage of the efficiency gains and testing opportunities that are afforded by pooled analysis.
Pooled analysis of individual-level data also has considerable appeal, but would require a substantially greater effort. An advantage of that approach is its ability to capture the influence of household demographic variables; this becomes a disadvantage, however, when the possibility that economic factors have a significant influence on household demographic variables is considered. Further, idiosyncratic variation in participation for individuals may mask the effects of state-level variables on participation; such variation is averaged out in aggregate state data.
Caseloads versus Openings and Closings
While some investigators have developed models of openings and closings rather than caseloads, difficulties in the administrative measures of openings and closings led us to conclude that it would be better to follow the direction taken by most investigators and model the size of caseloads directly. Despite these difficulties, it may well be worth developing an openings/closings model in the future.
Logs vs. Levels
While some researchers have used caseload levels for their dependent variable, many others have used logarithms. There is an important reason to use logarithms rather than levels in the pooled analysis: in a levels specification the coefficient of an explanatory variable estimates the effect of a unit change in the variable on the level of participation, while in a log specification it represent the percentage effect of a unit change. Looking across states that vary greatly in population size, the latter is more likely to be constant than the former. A reasonable alternative would be to use a caseload rate -- caseloads divided by the number of women in the relevant age group or some other measure of the at-risk population.
Mixing data with differing periodicities
One problem in specifying a quarterly or monthly model using state-level data is that quarterly or monthly data may not be available for some key variables. Other studies have addressed this problem by interpolating between annual data points. We have made substantial efforts to obtain quarterly data for many variables, but have had to resort to interpolation in a number of cases. This is especially unfortunate for variables that have lagged impacts on the caseload because the timing of major changes in the variable will not be captured accurately by interpolation methods. We necessarily are more skeptical about our findings for these variables than for others.
Notes
1. The model discussed is an update to the model described in CBO (1991). CBO staff have informed us that the CBO (1993) study has not been updated and that there are no immediate plans to update it in the future.
2. An analysis of Basic openings and closings appears in the appendix to CBO (1993). We discuss this analysis further in Section III.
3. Specifically, the disturbance term is assumed to have a "second-order autoregressive regressive" structure -- the current quarter's error is a linear function of the errors in the previous two quarters, plus a random error.
4. This variable is defined as the number of families headed by women with their own children under age 18, multiplied by the ratio of never-married mothers to ever-married mothers.
5. This discussion refers to the equation reported by Grossman (1985) in Table V.4. A latter specification omits some of the explanatory variables because forecasts of the omitted variables are not available.
6. The CBO sample period includes the entire sample period used by Grossman, plus an additional period of almost the same length (73 quarters for CBO versus 37 for Grossman).
7. An ARIMA model is an autoregressive integrated moving average specification--such data series are not stationary and differencing is required to convert them into a stationary series (an ARMA model) that can be modeled.
8. The Maryland model defines the real average monthly wages after taxes for the at-risk population as the average monthly wages of females in low-wage, female dominated industries (i.e., industries in which females represent at least 40% of the total work force) adjusted for the EITC, FICA, state income tax, and food stamp benefits.
9. Washington's FIP is virtually identical to the 1990 Family Support Act which created the JOBS program.
10. The requirement referenced is the stipulation that a household must have an income that is less than or equal to 150 percent of the state's standard of need before deductions -- known as the "150 percent rule."
11. We note that Grossman uses the level of unemployment in place of the unemployment rate in order to solve this scale problem for the unemployment variable.
12. Additional equations for Medicaid enrollees who are SSI recipients and "non-cash" Medicaid enrollees are also estimated.
13. The South dummy is omitted from the model with state fixed effects because that model already includes a dummy variable for each state.
14. See Moffitt (1992) for a review.
15. Fitzgerald estimates a hazard model of exits from AFDC. Using the results of his model, he simulates average survivor functions at 6, 12, and 24 months for particular variables, holding all other variables constant at their mean values.
16. See, for example, Blank and Ruggles (1996) and Hoynes and McCurdy (1994).
17. The categories of marital status used in this study are never married, divorced, widowed, and separated/other. Living arrangements are categorized as independent families, extended families, cohabiting with a single, unrelated adult male, and unrelated families.
18. Based on a phone conversation with Herbert Lieberman of the Office of Family Assistance in the Agency for Children and Families.
19. This type of variable, one that expresses earnings relative to AFDC benefits, is discussed further in the next section.
CHAPTER THREE: METHODOLOGY
A. INTRODUCTION
The methodology we use is technically described as "pooled cross-section time-series analysis" because it "pools" time-series data for a cross-section of individual states. We estimated the models using quarterly data for 51 "states" (including the District of Columbia) from 1979.4 through 1994.3 .
The methodology is described in generic terms here. Plans for the specifications of the dependent and explanatory variables are discussed in Chapter Four. We describe the econometric model in Section B. In Section C, we discuss the methodology we use to control for changes in the age distribution of the population. The construction of quarterly time series for explanatory variables that are only observed annually is discussed in Section D. The estimation methodology is discussed in Section E, and the simulation techniques are described in Section F.
B. ECONOMETRIC MODELS
We estimate separate Basic and UP models for caseloads, recipients, and child recipients. In addition, we estimate an average monthly benefit (AMB) equation for the combined programs. All equations are methodologically identical, differing only in the specification of their variables. In this section we first describe the "generic" structure of the equations.
Each equation estimated has the following general form:
Equation 3.1: Dln(Yst) = a1 Z1st + ... +a JZJst + b1 DX1st + ... + bKDXKst
+ g2Q2t + ... + g4Q4t + d80T80t + ... + d94T94t + est
where:
- Dln(Yst) is the change in the natural logarithm of the caseload, recipients, child recipients, or average monthly benefits in State "s" and from quarter "t-1" to quarter "t;"
- Z1st + ... + ZJst are dummy (binary) explanatory variables and current year values of selected "flow" variables (see below);
- a1 ... aJ are the coefficients of the dummy variables;?
- DX1st,..., DXKst are quarter to quarter changes in continuous explanatory variables. These include both current and lagged values for selected variables;
- b1,...,bK are the coefficients of the continuous explanatory variables;
- Q2t ... Q4t are quarterly dummy variables (the first quarter is the base quarter). Each dummy variable equals .25 for the quarter indicated by its name, and zero for all other quarters;
- g2 ... g4 are the coefficients of the quarterly dummies, interpreted as the difference between the annualized growth rate of Y in the reference quarter and the first quarter, other things constant;
- T80t ... T94t are year dummies, equal to .25 for every quarter during the reference calendar year, and 0 in all other quarters;
- d80 ... d94 are the coefficients of the year dummies, interpreted as the annual rate of growth in the first quarter of the reference year after controlling for other explanatory variables; and
- est is the regression disturbance.
The model is specified in changes in order to eliminate state "fixed effects" -- factors that vary across states, but not over time. "Time," or "year" effects are captured by the time dummies. Hence, we are essentially relying on covariation in changes across states to estimate the model's parameters. Purely cross-sectional covariation is not used at all, and use of purely time-series covariation to estimate parameters other than the year and quarterly dummy coefficients is minimal.(1)
We specify the dependent variable as a change in the logarithm because we expect the effects of changes in the explanatory variables to be proportional to the size of the caseload, rather than independent of the caseload size. For instance, a change in the maximum monthly benefit and a change in the unemployment rate are both expected to have an impact on caseload size that is proportional to the size of the caseload -- the more cases, or potential cases, that may be affected, the larger is the effect.
Some continuous explanatory variables are also in logarithms; for such variables the corresponding coefficient is an elasticity -- the percent change in the dependent variable per percent change in the independent variable. Those not in logarithms are all rates of some sort (e.g., the average benefit reduction rate).(2)
Continuous variables are specified in changes in most cases. Some "flow" variables -- representing potential case openings (e.g., immigrants) or closings -- are specified in levels. (3) The regression disturbance is assumed to follow a first-order autoregressive process, with different parameters in each state. Formally:
Equation 3.2: est = rsest-1 + vst,
where rs is the autocorrelation coefficient for state s (-1 < rs < 1), and vst is a random variable that is independent over time, but not across states. We assume that the variances and contemporaneous covariances of the vst are constant over time. This model is sometimes referred to as the "Parks" model (Parks, 1967).(4)
The Parks methodology has an important limitation -- the number of explanatory variables can be no larger than the number of time-series observations.(5) This prevented us from using the methodology for estimating models within subperiods and testing for stability across subperiods. (6) We did, however, estimate an UP model for all states using just the sub-period following the federal mandate, implemented in the fourth quarter of 1991, using an alternative specification. We assumed in this case that contemporaneous cross-state covariances of the disturbances are zero and that the autocorrelation coefficient is the same for all states. We also weighted each observation by the state's population.(7) To assess the influence of the alternative estimation methodology on the findings, we re-estimated our final caseload models for the full period via this method and compared the results to the Park estimates.
C. MODELING CHANGES IN THE AGE DISTRIBUTION OF THE POPULATION
The age distribution of the population has changed substantially during the period under examination as the "baby boom" generation has aged. Since the proportion of households on AFDC varies by the age of household head, we developed variables to capture the effects of population age distribution changes on AFDC participation. These variables also capture the effects of population growth. For each program (Basic and UP), we developed three "expected participation" variables -- one each for caseloads, total recipients, and child recipients. Construction of these variables is discussed in Section C.1, below.
A second, related, issue is that some explanatory variables in the model can be expected to change with changes in the age distribution (e.g., the unemployment rate), but such changes would not be expected to have an impact on AFDC participation -- although they might be associated with changes in participation because AFDC participation is affected by changes in the age distribution. When feasible, we adjusted such variables to remove the effect of age distribution changes. We describe the construction of the adjusted variables in Section C.2.
1. "Expected" Participation
The value of the expected participation variable for a specific State and quarter is the level of participation we would expect if age-specific participation rates were the same as national monthly average age-specific participation rates in 1990. We chose 1990 as the base year because the national age-specific data needed to construct the variable is better in that year than in others, due to the Decennial Census.
For the Basic caseload, the age-specific participation rate is defined as the number households in the Basic program headed by women in the age group divided by the number of women in the age group. Age-specific participation rates for the UP caseload are defined analogously, but using the number of households in the UP caseload, the age of the adult male in the household, and male population data. For expected recipients and expected child recipients in each program, we used the same scheme to classify households into age groups. The age-specific participation rate for recipients is the number of recipients in households in the age category divided by the number of women (Basic) or men (UP) in the age group, and the age-specific participation rate for child recipients is defined in the same way, but only including children. National age-specific participation rates for 1990 were estimated using the 1990 Survey of Income and Program Participation (see Chapter Four).
We constructed annual expected participation variables for each state by computing a weighted sum of the 1990 national age-specific participation rates, with the weight for each age group equal to the State's population of the relevant sex in the age category in the current year:
Equation 3.3: A*st = Sa Aa90 Past
where A*st is "expected" AFDC participation (i.e., expected caseload, recipients, or child recipients in one of the programs) in State s and year t, Aa90 is the 1990 national AFDC participation rate in age group a, and Past is the size of the population of the relevant sex in State s and year t that is in age group a. The final step was to convert the annual series to quarterly series, using the methodology discussed in Section E, below.
The change in the logarithm of each expected participation variable is used as an explanatory variable in the relevant participation equation. The coefficient of this variable can be interpreted as the percent change in the caseload associated with a one percent increase in the size of the population, holding the age distribution of the population and other explanatory variables constant. Hence, we would expect them to be close to one. In the initial models we estimated the coefficients of these variables were very significant, but not significantly different from one. In the models reported here, we have constrained the coefficient of these variables to be one.
2. Age-adjusted Explanatory Variables
Each age-adjusted variable is the logarithm of the ratio of the unadjusted variable to its "expected" value. Expected values are computed analogously to the computation of expected participation: they are a weighted average of age-specific national values for 1990, with the weight for each age group equal to the share of the State's population in the age category in the current year. Mathematically, the index variable (Xst ) is defined by:
Equation 3.4: Xst = ln(Wst / W*st)
where Wst is the unadjusted variable, and W*st is the "expected" value of the variable, defined as:
Equation 3.5: W*st = Sa Wa90 Past/Pst
where Wa90 is the 1990 national value of the variable for age group a and Pst is the total population of State s in period t. Thus, for example, the unemployment rate index for State A in 1982 is the log of the actual rate divided by the rate we expect given the age distribution of State A's working age population in 1982 and national unemployment rates by age in 1990. Annual figures were converted to quarterly series as described in Section E, below.
The complexity of the construction of each age-adjusted variable may diminish the ability of policy makers and others to understand and use the findings. The interpretation of the results and their potential use are not as difficult as they may first appear, however, and the results may be substantially more useful if adjusted variables are used than if unadjusted ones are used.
To illustrate, consider the logarithm of the age-adjusted unemployment rate as it would appear in a typical model:
Equation 3.6: ln(Ast) = ... + bu ln(ust/ust*) + ... = ... + bu ln(ust) - bu ln(ust*) + ....
where ust is the unemployment rate and ust* is the "expected" rate, defined as in Equation 3.5. It is apparent from the second representation of the unemployment term above that the coefficient of the age-adjusted variable can be interpreted as the elasticity of the caseload with respect to unemployment holding the other explanatory variables constant, and provided that the unemployment rate change is not due to a change in expected unemployment -- i.e., not due to a change in the age distribution of the population. This is no different than what the interpretation would be if we used the logarithm of the unadjusted unemployment rate as the explanatory variable, except in that case the interpretation would apply to changes due to changes in the age distribution of the population as well as any others. This also illustrates the reason for making an age adjustment: we would not expect a change in unemployment that is due to a change in the age distribution of the population to have the same impact on AFDC participation as a change that is due to the business cycle. In fact, we would expect it to have no effect other than the effect that is accounted for by the expected participation variables.
Continuing the illustration, contingency loans to States, intended to help them finance their AFDC payments during a recession, could be tied to the unemployment rate, with the maximum loan amount related to the gap between the unemployment rate and some "standard" unemployment rate. Some specific value for the unemployment rate would be the simplest choice for the standard rate, but the fact that unemployment rates vary because of changes in the age distribution of the population, not just because of the business cycle, means that the "standard" that would be appropriate for a given age distribution would be inappropriate for another one. The expected unemployment rate could be used as the standard instead, thereby recognizing the effect of a change in the age distribution of the population on the unemployment rate. Under the latter system, the maximum loan amount would be insulated from changes in the unemployment rate that are caused by changes in the age distribution of the population rather than by the business cycle.
D. MODELING DELAYED IMPACTS
There are strong reasons to believe that the impact of changes in many determinants of AFDC participation are delayed. The most prominent example is the unemployment rate; substantial evidence already exists that increases in the unemployment rate have their full impact on participation only after several quarters have passed (see Lewin-VHI, 1995a).
The simplest way to capture delayed impacts of a specific explanatory variable is to include "lagged" (i.e., previous period) values of the variable as separate explanatory variables. For instance, in all models we include the current quarter's unemployment rate, the previous quarter's rate ("first lag"), the rate from the second previous quarter ("second lag"), etc., for as many as nine quarters. If DlnUst-l is the change in the log of the age-adjusted unemployment rate lagged l periods, and bl is its coefficient, the unemployment rate specification can be represented as:
Equation 3.7: Dln(Yst) = ... + b0DlnUst + b1DlnUst-1 + ... bl DlnUst-l + ... bLDlnUst-L+ ....
where L is the longest lag length. The sum of the coefficients of the current and lagged coefficients is the total, or long-run, elasticity of a permanent increase in the age-adjusted unemployment rate.(8)
E. CONVERTING ANNUAL SERIES TO QUARTERLY SERIES
Some of the series to be used in the analysis are available annually only. In order to use them, we created quarterly series that fit the annual series exactly and that also follow a smooth pattern across quarters in each year. An example is a State's population in a specific age group. For most of the annual series, we utilized a method that first fits a smooth curve called a "cubic spline" to the annual series and then uses the fitted curve to generate quarterly series.(9) In some instances, however, this method produced unreasonable quarterly values. When this was the case, we used a method that first fits a linear spline to the annual series and then uses the fitted curve to generate the quarterly series.(10) The exact method applied to each series depends on the nature of the original series -- stock data are treated differently than flow data and "end-of-year" series are treated differently than "annual averages."(11) The fact that we had to estimate quarterly values from annual series implies that the quarterly values are measured with error. This specification presumably biases coefficients toward zero.
F. SIMULATIONS
We use the regression estimates to simulate the estimated effects of all explanatory variables, and selected subsets of the explanatory variables, on historical growth in AFDC participation over various subperiods of our sample.
For each simulation, we first calculate the change in the log of participation from the first quarter in the period to the last that is explained by the changes in the relevant explanatory variables by state. This change is divided by the number of quarters in the period and multiplied by four to get an estimate of the average annual rate of change due to the set of explanatory variables in the state over the period. We report these results directly for selected states.
To obtain a national average rate of change due to the explanatory variables, we compute the weighted average of the state changes using weights that are proportional to average participation in each state over the entire period.
Notes
1. If we had included a dummy variable for each quarter of the entire period, we would have eliminated entirely the role of purely time-series covariation in determining the coefficients. Our quarterly and yearly dummies are more restrictive than such a specification, but we think the difference is inconsequential. We also include separate dummies for OBRA81 and DEFRA84 in the reported results, to capture any nationwide effects of the implementation of those laws that was missed by the year and quarterly dummies. We also tried dummies for implementation of other legislation, but the estimated coefficients were not at all significant.
2. Grossman (1985) provides an example of a State model in which the dependent variable, caseloads, is in the levels. One of the explanatory variables in the model is a dummy for OBRA-81 implementation. The coefficient of this dummy represents the estimated effect of implementation on the level of the caseload in each State under the implicit assumption that the effect on the level is the same in all States. It would be more reasonable to assume that the effect in each State would be proportional to the size of the caseload -- the assumption implicit if the dependent variable were in logarithms.
3. We initially specified vital statistic variables -- marriages, out-of-wedlock births, and divorces -- in levels but switched to a change specification after finding that the latter had substantially more predictive power.
4. The autocorrelation parameter for each state could be negative because the dependent variable is a first difference. A value of zero in the first-difference specification corresponds to a value of one in a levels specifications. We estimated the model using the SAS/ETS, Release 6.10,procedure TSCSREG. We adjusted the standard errors and t-statistics obtained from SAS because of an error in the program that was confirmed by the SAS Institute. The standard errors reported by SAS were multiplied by [T/(T-P)].5, where T is the number of quarters in the sample period and P is the number of explanatory variables in the equation, and the t-statistics were divided by the same factor.
5. This limitation can be solved by imposing more structure on the variance and covariance parameters in the model, but this could not be implemented with TSCSREG.
6. For the same reason, we did not test for fixed state effects as originally planned. This would have required specifying the model in levels rather than changes and including 51 state dummies for the fixed effects, which was not possible given the length of the time series. Based on our earlier work concerning participation in SSA's disability programs, however, we were confident that we would not have rejected the fixed effect model.
7. The estimation was performed using the SAS procedure MODEL.
8. We initially planned to use polynomial distributed lags to impose some structure on the coefficients of the lagged unemployment rate variables because we expected collinearity among the lagged values to result in erratic patterns of the estimated coefficients. Collinearity was not, however, a serious problem, even with as many as nine lags.
9. The cubic spline specification requires each adjacent pair of annual observations to fall on a cubic function of time. The cubic function can be different for each adjacent pair, but the first and second derivatives of the two functions passing through a specific year's value are constrained to be the same.
10. The linear spline specification fits a continuous curve to the data by connecting successive input values with straight line segments. This method was used to produce the following quarterly series: IMMGTOTL, IRCA, MEDGAIN, MEDFAM3, SSIKIDS, and ZEBLEY. These variables are defined in Chapter 4.
11. This method is implemented using the EXPAND procedure in the Economic Time Series (ETS) component of SAS (see SAS/ETS Users Guide, 1993).
CHAPTER FOUR: VARIABLE SPECIFICATIONS
A. INTRODUCTION
In this chapter we describe the data set we have constructed for this project. Variable definitions and sources are listed in the Appendix. We discuss the dependent variables in Section B and explanatory variables in Section C.
B. DEPENDENT VARIABLES
For both the Basic and UP programs, we estimate three participation models: caseload, total recipients, and child recipients. In addition, we estimate an average monthly benefit per family (AMB) for the combined programs. We have defined the dependent variables for each model as follows:
- Caseload -- the natural logarithm of the average monthly caseload (i.e., families receiving a payment of at least $10 during the month) in the program during the quarter.(1)
- Total Recipients -- the natural logarithm of the average monthly number of recipients (i.e., individuals in families receiving a payment of at least $10 during the month) in the program during the quarter.
- Child Recipients -- the natural logarithm of the average monthly number of child recipients ( i.e., children in families receiving a payment of at least $10 during the month) in the program during the quarter.
- Average Monthly Benefits (AMB) -- the natural log of the combined average monthly payment per family for the Basic and UP programs during the quarter divided by the appropriate regional CPI-U, for each program.(2)
We acquired electronic caseload data from the Administration for Children and Families (ACF) for both the Basic and UP programs, by month, for the period from October 1978 through March 1995. ACF likewise provided us with total recipient data for both the Basic and UP programs for the period from October 1982 through March 1995. ASPE supplemented the ACF data with total recipient data extracted from the database assembled by Grossman (1985) for the period from January 1978 through September 1982. ACF also supplied us with child recipient data from January 1978 through March 1995. We received these data in a combination of electronic and hard copy formats. All participation data used in the model match those published in the ACF publication Quarterly Public Assistance Statistics and its monthly predecessor, Public Assistance Statistics.
The state-level AMB data are for the period from 1980.1 through 1993.4 only, and were obtained from numerous editions of Quarterly Public Assistance Statistics.
We obtained the regional CPIs electronically from the Bureau of Labor Statistics. There are indices for four regions: North East, North Central, Southern, and Western. The regional CPIs appear bimonthly from 1980 through 1986 and monthly from 1986 to the present. We calculate quarterly values from the bimonthly/monthly indices.(3)
C. EXPLANATORY VARIABLES
Four types of explanatory variables appear in the models:
1. Demographic variables;
2. Labor market variables;
3. AFDC program variables; and
4. Variables for other programs and state laws.
We discuss the construction and use of these groups of variables below.
1. Demographic Variables
We group demographic variables into two subgroups: population characteristics and vital statistics. Population characteristics include the size of the population by age and sex, while vital statistics (e.g., out-of-wedlock births) refer to the structure of families. Population characteristics appear in all models. We have, however, explored the extent to which changes in economic factors affect AFDC caseloads and spending through their impact on family characteristics by including these characteristics in some models, but not in others
a. Population Characteristics
A general description of the methodology we use to capture the effects of population characteristics appears in Chapter Three. Recall that this requires the construction of "expected participation" variables, plus age adjustments to selected economic variables. We provide more details on the construction of expected participation variables here; details of the age-adjustments appear in later discussions of the variables to be adjusted. We also discuss the immigration variables here.
Expected Participation
The state-level population characteristic estimates needed for constructing the expected participation variables are available only on an annual basis. Hence, we have constructed an annual average monthly participation series for each program and then expanded the series to a quarterly series, using the methodology described in Chapter Three.
The following is a description of the construction of the expected Basic and UP caseload variables. Calculation of the expected total recipient and child recipient variables follows this same methodology (see the Appendix).
We employ three types of data to construct the expected caseload variables. The first type is AFDC participation by type of family (one-parent versus two-parent) and age of head for 1990, estimated using the 1990 Survey of Income and Program Participation (SIPP).(4) We use the SIPP data to compute initial national age-specific participation rates in the base period for the two programs. The rate for the Basic program in each specific age group is the proportion of women in an age group who head a one-parent AFDC family. The corresponding initial rate for the UP program is the number of men in the age group who are a parent in a two-parent AFDC family.(5)
The second type of data is national Current Population Estimates by age and sex in 1990 from the Bureau of the Census, and were used to control our initial participation rate estimates to national totals. For the Basic program, we multiply the initial age-specific participation rates by the number of women in the corresponding age group and then add across age groups to get implied estimates of the national Basic caseload in the base period. We then adjust all of the initial age-specific participation rates by the ratio of the actual caseload average monthly caseload for the period (from ACF statistics) to the estimated caseload. We repeat this process for the UP program, but using age-specific estimates for the number of men.
The third type of data is state Current Population Estimates by age and sex, from the Bureau of the Census, used with age-specific participation rates to construct the expected participation series for each state. For the Basic program, we multiply the age-specific participation rates for the base period by the number of women in the corresponding age group for each state and quarter and then add across age groups to obtain the value for the expected Basic caseload in that state for that quarter. We follow this same procedure for the UP program, but using the population estimates for men.
Immigration
We employ two measures of immigration in our models: the total number of immigrants by state and the number of aliens per thousand population legalized under the Immigration Reform and Control Act (IRCA) of 1986. We obtained fiscal year data for both series from the Immigration and Naturalization Service (INS). INS data for total immigrants cover the period from FY1978 through FY1994 while data for IRCA legalizations cover the period from FY1989 through FY1994; no IRCA legalizations occurred before FY1989. We interpolate quarterly values for each variable from the fiscal year series to obtain the series used in the models. We experimented with several variants of the IRCA variable including lagged and lagged moving average constructions. The final construction included in the models is the movement of the four previous quarters.
b. Vital Statistics
The number of female headed households with children under the age of 18 has proven to be a strong predictor of AFDC Basic participation in previous studies. Unfortunately, reliable estimates of the number of female headed households at the state level are unavailable. Therefore, we relied on variables constructed from state-level vital statistics on marriages, divorces, and out-of-wedlock births to proxy for female-headed households in our Basic models.(6) The quarterly series used in the model are interpolated from the annual data provided by the Natality, Marriage, and Divorce Statistics Branch, National Center for Health Statistics. We also tried a "marriage market" variable in some models.
We expect the changes in the vital statistics variables to result in changes in the number of female headed households and, consequently, have an impact on the Basic caseload. We estimated Basic participation models with and without these data to determine whether the coefficients of business cycle variables are sensitive to their inclusion. It could be that business cycle effects work, in part, through their effects on formation of female-headed households. We also explore the effects of these factors in our UP models because changes in the number of two-parent households are expected to affect UP participation. In addition to the current values of these variables, we experimented with both multiple lag and lagged moving average specifications. In the results reported we use the moving average of the four previous quarters.
At least one previous study of participation in the AFDC has included a measure of "marriage market conditions" as an explanatory variable (Shroder, 1995). The variable used is a mixture of a demographic variable and an economic variable: the log of the number of women between the ages of 15 and 64 in the state divided by the number of employed men in the state. We obtained annual state-level employment data by sex from the Bureau of Labor Statistics (BLS) and annual state population data by age and sex from the Bureau of the Census to create an annual series. The quarterly series included in the models is interpolated from this annual series. We experimented with a few variants of this variable, including lag specifications and the moving average of the last four quarters.
2. Labor Market Variables
We assess the explanatory power of several labor market variables in our models:
1. the unemployment rate;
2. unemployed persons, total and per capita;
3. employed persons, total and per capita;
4. persons employed in trade industries, total and per capita;
5. persons employed in manufacturing industries, total and per capita;
6. average weekly wage in retail trade industries; and,
7. average weekly wage in manufacturing industries.
We obtained monthly, state-level unemployment rate data from BLS for the period from January 1976 through December 1994. We converted this series to a quarterly series by averaging the monthly values within a given quarter. The specification used in all models is age-adjusted: the log of the actual value for each quarter divided by an expected value for the quarter.
The expected value is constructed at an annual level first, using national unemployment rates by age and sex for 1990 and state population data by age and sex for each year, then interpolated to get quarterly figures. As discussed in Chapter Two, substantial evidence already exists that increases in the unemployment rate have their full impact on participation only after several quarters have passed, and therefore we experimented with various lag specifications for this variable.
We similarly obtained monthly data series for total employment, employment in trade, and employment in manufacturing from the BLS for the period from January 1976 through December 1994. We converted these monthly series to quarterly series by averaging the monthly values within a given quarter. The total unemployment series was calculated from the total employment and unemployment rate series.(7) The per capita series were obtained simply by dividing by the state population and then multiplying by 1000. All variables were entered in log form. As with the unemployment rate variable, we experimented with various lag specifications for these variables.
Annual average-weekly wage data at the state level for both the retail and manufacturing industries were obtained from BLS for 1978 through 1994. The quarterly values used in the model are interpolated from the annual series and then divided by the appropriate regional CPI-U. The variable as it appears in the models is equal to the log of the real wage.
Following previous researchers (Chapter Two), we initially used the retail wage variable for the Basic model and the manufacturing wage variable for the UP model. As with the unemployment rate variable, we experimented with various lag specifications of the wage variables.
3. AFDC Program Variables
In Chapter One we presented a stylized, but essentially correct, version of the budget constraint for an AFDC household. Ignoring the value of Medicaid benefits, which we consider separately, the constraint reflects earnings, AFDC cash payments, the value of Food Stamps, the earned income tax credit (EITC) and payroll (FICA) taxes. The stylized constraint is characterized by four parameters: the maximum monthly benefit (MMB), the average tax and benefit reduction rate (ATBRR), the marginal tax and benefit reduction rate (MTBRR), and the gross income limit (CUTGIL). We constructed quarterly series for the first three of these parameters for each state using program data. For CUTGIL, which may be inconsequential in some cases, but binding in others, we constructed a measure of how restrictive the limit is likely to be. One of the four series, MTBRR, varies relatively across states in any given year during the sample period and, therefore, is not used in the models we report.(8)
In addition to these four parameters, we constructed a series of dummy variables to capture the effects of program changes that are not fully reflected in changes to the parameters.
a. Program Parameters
All of the program parameters are for a hypothetical AFDC family of three -- one parent and two children.
Maximum Monthly Benefit
The most commonly used program parameter in past studies is the maximum monthly benefit (MMB). The reasons for this may be that: it is intuitively appealing; the data are easily constructed; MMB varies substantially both across states and over time; and the MMB may be highly correlated with other aspects of the program that determine both eligibility and benefit levels.
We define MMB as the typical maximum AFDC benefit for a three-person family during the quarter plus the value of Food Stamps for a family receiving that benefit, deflated by the regional CPI-U.(9) If a state changes its nominal AFDC payment rate during the quarter, we use the average rate applicable over the three months.
We use several data types and sources to create the MMB variable. ACF provided us with state-level typical maximum monthly payment (MAXPAY) data for a family of three from 1979 through 1994. Quarterly MAXPAY data were not compiled before July 1982; therefore, we estimated quarterly MAXPAY values from 1979.1 to 1982.2 based on historical state fiscal year budgeting patterns.(10) We obtained maximum monthly Food Stamp benefit and standard deduction data by quarter from the Program Reports and Analysis Branch, USDA. The Food Stamp benefit for a three-person family receiving the typical maximum AFDC benefit is equal to the maximum Food Stamp benefit for a three-person family less 30 percent of the difference between MAXPAY and the Food Stamp standard deduction.
For practical reasons, our treatment of other program variables is not symmetric with our treatment of the MMB measure in that we do not assume they are simultaneously determined with participation and average monthly benefits. Instead, we treat them as exogenous, with some risk of reporting findings that are biased estimates of their impact on participation.
Average Tax and Benefit Reduction Rates
The average tax and benefit reduction rate (ATBRR) is the average rate at which disposable income is reduced per each dollar of income, earned or unearned, between zero earnings and the AFDC "earnings cut-off" -- the highest level of gross earnings that a family of three can have and still receive some benefit . Formally:
Equation 4.1: ATBRR = 1 - (Yc - Y0)/Ec,
where Yc is disposable income at the earnings cut-off, Y0 is disposable income at zero earnings, and Ec is the AFDC earnings cut-off. We define disposable income as the sum of earnings, EITC, AFDC benefits, Food Stamp benefits, and less FICA where the AFDC benefit is calculated using the earnings disregard for a family that has received AFDC benefits for more than 12 months. Thus, Y0 is identical to MMB.
ATBRR varies across states as a result of a state's MMB, earnings cutoffs, and other program characteristics. ATBRR also varies over time within states as a result of federal program provisions, most notably OBRA81 and DEFRA84, and changes in the EITC. These latter changes had differential effects across states because of the initial cross-state variation in the variable. This is especially true for OBRA81. We experimented with various lags of ATBRR in the models.(11)
Marginal Tax and Benefit Reduction Rate
The marginal tax and benefit reduction rate (MTBRR) is the rate at which disposable income decreases for each additional dollar of earnings; we calculated the MTBRR for the level of earnings just below the AFDC earnings cut-off. Specifically,
Equation 4.2: MTBRR = 1 - (Yc - Yc-20)/20,
where, Yc is disposable income at the earnings cut-off, and Yc-20 is disposable income at $20 below the AFDC earnings cut-off.(12) Like ATBRR, MTBRR is sensitive to both state and federal program provisions. We experimented with various lags of MTBRR in the models.
Gross Income Limit
Prior to October 1, 1981, there was no federal provision for a gross income limit at which families became ineligible for AFDC benefits. In some states, families with very substantial earnings could obtain AFDC benefits because of income disregards for employment expenses and child care. OBRA81 imposed a limit on the gross income that a family could have and still received any benefit, at 150 percent of the state's need standard; i.e., a family became ineligible for AFDC benefits if its income exceeded 150 percent of the applicable need standard. DEFRA84 raised the gross income limit to 185 percent of a state's need standard.
The practical effect of a federally mandated gross income limit varies across states and is dependent on the level of the gross income limit in relation to the AFDC earnings cut-off. In fact, the gross income limit enacted under OBRA81 exceeded the AFDC earnings cutoff for our hypothetical family in every state. We have assumed very small disregards however -- the monthly standard allowance after twelve months of receiving benefits and no child care.(13) If the same family had substantially greater employment or child care expenses, the gross income limit might have been binding in many states after OBRA81, and in fewer states after DEFRA84. The closer a state's gross income limit is to the AFDC earnings cutoff we have computed, the more likely it is to be binding.
To reflect these considerations, our measure of how binding the gross-income limit is in a state, CUTGIL, is equal to the AFDC earnings cutoff relative to the gross income limit. Prior to 1981.4, CUTGIL is equal to zero in all states because the gross income limit during that period was, implicitly, infinity. The larger this ratio is, the more likely the gross income limit is binding for some potential AFDC families.
b. Dummy Variables for Other Program Features
The Unemployed Parent Program
The introduction of the Unemployed Parent (UP) program in a state may reduce participation in the Basic program. It may also reduce the sensitivity of participation in the Basic program to changes in the labor market -- in the absence of the UP program, the best option for a pair of unemployed parents may be to not marry, or to get divorced, so that the mother and children can obtain Basic benefits.
In addition, the length of UP program benefits may have a significant impact on participation in the both programs. FSA88 requires that states provide benefits for a minimum of sixth months per year; many states, however, provide benefits for the entire year, and states with 12-month programs before October 1, 1990 were required to continue 12-month programs under FSA88.
To gauge the effects of both the existence and the length of UP programs, we include two separate dummy variables in our Basic models: UP12M and UP6M. UP12M, is equal to one in those quarters during which a state administers an UP program with no time-limited eligibility; otherwise, it is equal to zero. Similarly, UP6M is equal to one in those quarters during which a state administers an UP program limiting eligibility to six months out of every twelve months and equal to zero elsewhere.
It is possible that UP programs introduced in 1990 under Federal mandate have different impacts on participation than those introduced voluntarily by states in earlier years, holding the months of coverage constant. States may, for instance, introduce a Federally mandated program in a way that minimizes its fiscal impact on the state's budget, whereas states may place more weight on other objectives in implementing a voluntary program. Hence, we define a third UP dummy, UP90, to distinguish programs that were introduced in the fourth quarter of 1990, under the Federal mandate, from others.
Implementation of New Federal Requirements
Changes were made in federal AFDC requirements under each of the following acts during the 1980-95 period: the Omnibus Budget Reconciliation Act of 1981 (OBRA81), the Deficit Reduction Act of 1984 (DEFRA84), OBRA87, the Family Support Act of 1988 (FSA88), OBRA90, and OBRA93 (Committee on Ways and Means, 1994).
To some extent, the effects of these changes in Federal requirements are captured through changes in the program parameter variables - especially the ATBRR and CUTGIL. Furthermore, the methodology used to model the UP program also captures one of the major changes mandated by FSA88. Other provisions of these acts, especially the JOBS program and the Medicaid and child care expansions mandated by FSA88, are not, however, captured in these variables. The year dummies may also capture some of the effects of these acts to the extent that the effects are proportional and contemporaneous in all states. Recall, however that the year dummies are constrained to be the same in each quarter of the year, so their ability to capture the proportional, contemporaneous effects of a requirement that is implemented in a specific quarter is limited.
We experimented with nine different dummy variables related to federal AFDC requirements. They are:
1. OBRA81;
2. DEFRA84;
3. OBRA87;
4. MEDCCXPN, for effects of transitional Medicaid and child care expansion provisions in FSA88;
5. JOBS, for effects of implementation of state job programs;
6. FSAUP1, for effects of FSA88 provisions requiring states implement UP programs;
7. FSAUP2, for effects of work and educational program requirements in FSA88 for UP families;
8. OBRA90, for the exclusion of any children receiving foster care maintenance or adoption assistance payments from the AFDC assistance unit mandated under OBRA90; and,
9. OBRA93.
Details for each variable appear in the Appendix. With two exceptions, all of these variables change from zero to one in a specific quarter in all states -- the quarter of implementation. The first exception is JOBS which changes from zero to one in the quarter during which a state initiated its JOBS program. The second exception is FSAUP1 which changes from zero to one in 1990.4 for states with no UP program before the federal mandate. FSAUP1 equals zero throughout for those states with UP programs before October 1990. We experimented with lagged specifications for some of these variables, on the assumption that the full impact of implementation on participation or average monthly benefits did not occur in the first quarter of implementation.
Waivers
Many states have obtained and implemented waivers to federal rules under Section 1115 of the Social Security Act ("1115 Waivers") during the period under investigation, especially during the last few years. Based on descriptions of all waivers granted during this period provided by ACF, we identified those waivers that were both implemented for a large share of the state's population at some point during the sample period and expected to have an impact on participation and/or average monthly payments.(14) We have grouped these waivers into five categories based on the provisions of the waivers, and have created a dummy variable to capture them:
- NOKIDS is a dummy for waiver provisions reducing or eliminating AFDC benefits for children born or conceived while the family is receiving AFDC;
- WORKREQ is a dummy for waiver provisions requiring AFDC recipients to engage in work, education, or training activities outside of those under the state's JOBS program;
- MEDEXPAN is a dummy for waiver provisions extending transitional Medicaid benefits for an additional one to two years;
- UP100 is a dummy for waiver provisions eliminating the 100-hour work limitation rule for AFDC-UP eligibility; and
- UP100WH is a dummy for waiver provisions eliminating both the 100-hour work limitation rule and the work history requirement for AFDC-UP eligibility.
The dummy for a particular waiver equals one in each state that implements the waiver (sometimes just one state) for all quarters from the first quarter of implementation in the state forward, and is zero for all earlier quarters; the dummy's value is zero in all quarters for all other states. This specification assumes a once and for all proportional change in participation and/or average monthly benefits as the result of the waiver. We also experimented with lagged values of the dummies to allow for transitional effects. See the Appendix for further details.
4. Other Program Variables and State Laws
All of the following programs are either substitutes or complements for AFDC: Medicaid, general assistance (GA), Supplemental Security Income (SSI), and unemployment insurance (UI). That is, these programs provide benefits to some members of AFDC families that, in the case of substitutes, are counted against AFDC benefits (GA, SSI, and UI) or that, in the case of complements, are obtained because the family receives AFDC (Medicaid). All of these programs changed substantially in at least some states during the sample period, and we attempt to capture the effects of these changes on AFDC participation and average monthly benefits through a set of program variables. Note that we also take the effects of changes in the Food Stamp program into account via adjustments to the maximum monthly AFDC benefit variable.
We also attempt to estimate the impacts of state laws concerning establishment of paternity; enforcement of child support; and limits on abortions on AFDC participation and/or average monthly benefits. The variables we develop to capture changes in other programs and changes in state laws are described below.
a. Medicaid
We use three Medicaid variables. The first is an estimate of the value of Medicaid benefits for an AFDC family with an adult and two children. Other things equal, we expect increases in this variable to increase participation. Robert Moffitt has constructed a similar variable valuing the Medicaid benefits for an AFDC family with an adult and three children (Personal correspondence with Robert Moffitt). Following Moffitt's' methodology, our Medicaid benefit for a family of three equals the mean Medicaid expenditures for AFDC mothers in a state plus two times the mean for AFDC children. The raw data for this variable are for fiscal years and come from Form HCFA-2082 Data Tables. We interpolate quarterly values from the fiscal year series and deflate the value by the appropriate regional CPI-U to obtain the series used in the model. We use the logarithm of this variable in the model.
The second Medicaid variable is intended to capture the potential effects of expansions of Medicaid benefits to low-income mothers and children who are not AFDC eligible, under OBRA86, OBRA87, OBRA89 and OBRA90. At our request, Aaron Yelowitz has compiled a measure of the share of children affected by these expansions for the years from 1988 to 1993, using data from the March Current Population Surveys and information about the expansions that he had compiled in the process of analyzing this issue using micro data (see Yelowitz, 1994). The measure is the percent of children made eligible for Medicaid whether or not they are in an AFDC household. We assume that the share is zero in every state before 1988, although a small number of children under the age of two and living in families with incomes below the federal poverty line were eligible in some states. We interpolate quarterly values from the annual series we received from Aaron Yelowitz to obtain the series used in the model. We experimented with several specifications of this variable including lagged specifications and the moving average of the previous four quarters.
The third Medicaid variable is a dummy variable representing restrictions on Medicaid funding for abortions. Because restrictions and the exact wording of Medicaid funding guidelines vary substantially by state and over time, it would be possible to group states into several different categories based on the relative restrictiveness of their guidelines. For this analysis, however, we simply construct a dummy variable identifying the existence of state Medicaid policies that deny payment for "therapeutic" abortions.(15) Medicaid programs not paying for "therapeutic" abortions maintain "substantive restrictions" on funding, permitting Medicaid funding of abortions only to save the life of the mother, to prevent "substantial physical health hazard," in the case of severe fetal deformity, and/or when a pregnancy is a result of rape or incest. We construct this variable based on month specific data obtained from Merz, et al (1995). For each state, the dummy variable is equal to one in those quarters during which the state refused Medicaid funding for therapeutic abortions. Otherwise, the variable is equal to zero.
The directions of the effects of such restrictions on AFDC participation and average monthly benefits are uncertain, in part because the directions of the effect on fertility are uncertain. Recent studies by Hass-Wilson (1996) and Currie, Nixon, and Cole (1995) show a negative relationship between restrictions on Medicaid payments for abortions and the share of pregnancies that are terminated by abortion. However, more restrictive abortion funding policies may also reduce pregnancies by increasing the risk or cost associated with pregnancy. The effect on AFDC participation is also ambiguous because the benefit is of little value to a pregnant mother unless she is already a participant. The effect on average monthly benefits is likely to depend on the effect on fertility -- if the mean number of children increase, the value of the benefit will increase.
b. General Assistance
In our previous work on SSA's disability programs, we identified 20 instances in which individual states significantly reduced their general assistance (GA) caseloads between 1980 and 1993 (Exhibit IV.E.1 in Lewin-VHI, 1995b). The termination of Michigan's GA program in 1991 resulted in the largest single reduction on a per capita basis, over 15 per thousand population, but five other reductions exceeded seven cases per thousand. Four of these six very large cuts occurred in 1991 or 1992. We also found one instance of a substantial increase in a state's program.
We have constructed a "GA reductions" variable to use in the AFDC model following the same methodology that we used in our disability program work. In each state, the GA change is zero in the first quarter of the sample period. When a GA cut or increase occurs in a state, we measure the size of the cut per capita as the difference between the average monthly GA caseload in the three months following the quarter in which the change occurred and in the three months preceding that quarter, divided by the state's population (Exhibit 4.1). The value of the GA reductions variable is set equal to the resulting number for the quarter in which the change occurred. We also experimented with lagged values of this variable.
Exhibit 4.1
General Assistance Caseload Reductions, 1980 - 1993
| State | Year.qtr | GA Caseload Reductions* | Cuts per Thousand** |
| Delaware | 1985.1 | 1,159 | 2.98 |
| District of Columbia | 1981.2 | 790 | 1.88 |
| 1992.1 | 1,330 | 3.40 | |
| Illinois | 1992.3 | 45,421 | 6.39 |
| Indiana | 1987.1 | 26,535 | 7.93 |
| Kansas | 1987.2 | 1,852 | 1.27 |
| Louisiana | 1986.1 | 1,679 | 0.64 |
| Maine | 1992.3 | 4,070 | 5.34 |
| Maryland | 1992.4 | 1,307 | 0.42 |
| 1993.4 | 2,276 | 0.72 | |
| Massachusetts | 1992.2 | 7,216 | 1.91 |
| Michigan | 1992.1 | 90,946 | 15.73 |
| Minnesota | 1984.3 | -9,512 | -3.78 |
| 1992.1 | 14,424 | 5.34 | |
| New Hampshire | 1981.3 | 394 | 0.68 |
| Ohio | 1992.2 | 66,834 | 9.92 |
| Oklahoma | 1986.3 | 1,247 | 0.64 |
| Pennsylvania | 1983.3 | 49,774 | 6.88 |
| Rhode Island | 1993.4 | 4,050 | 6.59 |
| Virginia | 1992.2 | 2,947 | 0.71 |
| West Virginia | 1987.1 | 2,146 | 1.9 |
* GA caseload reductions are calculated as the reduction in the average monthly GA caseload from the three months before the quarter in which the change occurred to the average in the three months following that quarter. This difference was calculated only for those states which substantially changed their GA caseloads during a year and for which we were able to confirm a program change.
**Cuts per thousand are GA caseload reductions divided by the population (in thousands) age 18 to 64.
Source: Administration for Children and Families and Lewin-VHI calculations.
We consistently found strong evidence that GA reductions were associated with increases in SSI participation in our earlier analysis (Lewin-VHI, 1995b, 1995d). We expected weaker results for AFDC because GA programs generally serve adults who are not custodians of children. It is also possible that GA reductions are associated with reductions in AFDC caseloads and payments because states that are making programmatic changes to reduce GA spending may be making analogous changes to reduce AFDC spending. If the latter changes are not fully captured in the AFDC program variables, they may be captured by the GA change variable.
It must be recognized that the GA change variable is a crude measure of changes in GA programs, for several reasons. First many states do not have state-wide programs. Although major counties in such states often do have programs, their caseloads are not included in the state statistics used to construct the GA change variable. Second, this variable does not distinguish between the many different methods used to reduce caseloads (e.g., time limits versus "able-bodied" restrictions versus reductions in benefit levels). Presumably the size of any effect of a reduction on AFDC would depend on the nature of the reduction, as well as its size.
c. Supplemental Security Income
Parents and children with sufficiently severe disabilities in AFDC families are eligible for SSI. While individuals cannot receive benefits from both programs, families can -- family members who are receiving SSI benefits are not counted in the AFDC family unit. Although SSI benefits are greater than AFDC benefits, AFDC family members who qualify for SSI may not apply for benefits, for a variety of reasons: the SSI application process is difficult and the outcome is uncertain; parents may be unaware that they or their children qualify; or parents may be misinformed about the effect of obtaining SSI benefits on AFDC eligibility and benefits for other family members.
Increases in SSI benefits would presumably increase the number of individuals in AFDC families that obtain SSI benefits, and therefore reduce average monthly payments. In some cases, the whole family may switch, thereby reducing the AFDC caseload. Changes in the determination of disability for SSI could also have an impact on AFDC payments and participation.
The federal SSI payment schedule has not changed in real terms since the inception of the program in 1974. Many states supplement the federal payment, however, and over the period under examination the real value of the sum of the supplement and the federal benefit have changed substantially in some states. In our work on SSA's disability programs, we found that increases in the real value of the maximum SSI payment (federal plus state supplement) relative to average monthly earnings were strongly associated with increases in SSI participation.
Here, we use the log of the maximum payment variable as an explanatory variable. Other things constant, we expect to find a negative, but relatively weak, association between this variable and AFDC caseloads, and a stronger negative relationship between the same variable and recipients, child recipients, and average monthly benefits.
Changes in SSA's criteria for determining whether an individual has a sufficiently severe disability to qualify for SSA may also have an impact on AFDC participation and benefits. In 1990 and 1991 the eligibility criteria for children were expanded substantially as a result of the Supreme Court decision in the case of Sullivan v. Zebley, and subsequent changes to the criteria for determining the severity of mental illness among children. There were large increases in the number of child SSI recipients in all states, and there is anecdotal evidence that many of the new child SSI recipients came from AFDC families. Thus, during this period especially we would expect an increase in child SSI recipients to be associated with a decline in child AFDC recipients, total recipients, average monthly benefits, and perhaps even caseloads.
We use two alternative variables to try to capture any impact of SSI expansions for children on AFDC participation and expenditures. The first is the number of child SSI recipients. We obtained data on SSI child recipients for December of each year from 1977 through 1994 from the Social Security Bulletin, Annual Statistical Supplement. The second variable is the number "Zebley children," children who received an SSI award as direct consequence of the Zebley. Charles Scott of the Social Security Administration provided us with data on SSI Zebley child recipients for June and December of each year from 1991 through 1994. We interpolated both biannual series to construct quarterly series.(16) In the final series, the variables are equal to the natural logarithm of the average monthly number of SSI child recipients in the given quarter and the natural logarithm of the average monthly number of SSI Zebley child recipients in the given quarter. We experimented with several specifications of these variables including lagged specifications and moving averages of the last four quarters.
d. SSA Allowance Rates
Between 1977 and 1978, the Social Security Administration's tightening of eligibility criteria for SSDI and SSI resulted in a decrease in initial allowance rates. While SSA mandated the tightening, it was implemented by state Disability Determination Services at different times and with differing intensities (see Parsons, 1991). We have created a variable to gauge the extent to which this administrative tightening may have increased AFDC participation as families denied SSDI or SSI benefits sought alternative sources of income. This variable is equal to the decrease in the SSDI allowance rate in a given state between 1977 and 1978 interacted with the calendar year dummy variable for 1980. Allowance rate data for Alaska, the District of Columbia, and Hawaii were not available, so we created a separate dummy variable for each of these areas equal to one during 1980 and zero in all other years.
e. Unemployment Insurance
If a newly unemployed parent in a potential AFDC family receives unemployment insurance (UI) benefits, the family is less likely to qualify for AFDC benefits than otherwise. We expect, therefore, that the impact of increases in the unemployment rate on AFDC caseloads would be inversely related to the share of unemployed persons who receive UI benefits. We also expect an inverse relationship between the share of unemployed persons with UI benefits and average monthly AFDC payments because UI benefits paid to AFDC family members reduce the size of AFDC benefits dollar for dollar. Because UI benefits are time limited (six months under normal circumstances in almost all states), the strength of these inverse relationships is likely to diminish substantially after two quarters. Extensions of UI benefit periods during severe recessions (usually an additional quarter) may increase the number of quarters over which the relationships are observed -- from one or two to three or four.
While the direction of the effects of an exogenous increase in UI benefits on AFDC participation and AMB seems clear, there is an important reason why we might not obtain findings that are consistent with expectations. UI program changes may mirror AFDC program changes in states. For instance, states that administratively tighten award of UI benefits out of fiscal necessity are likely to do the same for AFDC benefits. If such changes in the AFDC program are not captured in the AFDC program variables, changes UI program variables may proxy for them. Thus, tightening of UI benefits might be associated in the data with reductions in AFDC participation, rather than the hypothesized increase.
Like AFDC, the UI program is a state-federal program. Each state's program must comply with federal regulations and reporting requirements, but states have substantial latitude within those requirements concerning benefit eligibility and levels. Ideally, we would capture the essential program characteristics of state UI programs in one or two explanatory variables. We explored this approach during our work on participation in SSA's disability programs and found it infeasible, both because of the complexity of state programs and because of limitations on data availability. Hence, we adopted a simpler approach: we include the logarithm of the insured unemployment rate divided by the total unemployment rate as an explanatory variable in both the participation and average monthly benefit equations. Like the unemployment rate, the insured unemployment rate is available from the BLS, monthly. We use the average of each quarter's three months to construct the variable. We experimented with both current and lagged values of the constructed variable.
Because the UI measure is based on actual participation, it is especially susceptible to the problem discussed above -- reductions in the share of unemployed persons who are covered by UI may reflect administrative tightening or other factors that have a common effect on both AFDC and UI, inducing a positive relationship between the UI measure and AFDC participation.
f. Child Support Enforcement Laws
Laws that effectively increase child support are likely to reduce AFDC participation and average monthly benefits in two ways. First, as suggested by Gaylin and McLanahan (1995), they may reduce fertility by increasing the cost of fatherhood to men, and thus reduce the number births to unmarried mothers. Second, increases in actual and reported income from other sources for (potential) AFDC families would reduce AFDC payments. Furthermore, a sufficiently large increase would make the family ineligible for AFDC.
Gaylin and McLanahan (1995) analyze the impact of three child support enforcement (CSE) laws on nonmarital birth rates: presumptive guidelines, immediate wage withholding, and paternity long-arm statutes. Their results demonstrate that states with CSE statutes experience lower nonmarital birthrates (Gaylin and McLanahan, 1995). The authors have provided us with data detailing which states have enacted each of these laws and in which year they were enacted. In addition, Mr. Gaylin has given us data on mandatory withholding laws. We created dummy variables for all four types of CSE laws and initially include all four in all of the participation and AMB equations. Because we only know the year in which each statute went into effect, we assume that each became effective on January 1st of the known year.
g. Restrictions on Abortions
In addition to restricting Medicaid payments for abortions, many states have enacted laws regulating minors' access to abortion services. Twenty-four states enforced parental consent and/or parental notification laws for at least part of the period from 1980 through 1994. For this analysis, we treat parental consent and parental notification laws collectively as parental involvement laws based on the assumption that both types of laws have very similar impacts on fertility rates. Using data compiled in Merz, et al (1995), we have a constructed dummy variables denoting the enforcement periods of such laws.
As with the effects of Medicaid funding for abortions on the overall fertility rate, the effect of parental consent or notification laws on fertility among minors is uncertain. Haas-Wilson (1996) finds that the enforcement of such laws decreases the number of abortions per live births among minors. However, such laws may also decrease the fertility rate among minors by restricting minors' options and, thus, increasing the costs associated with becoming pregnant.
Notes
1. Each month's figure receives a weight equal to the ratio of the number of days in the month to the total number of days in the quarter in computing the average monthly caseload.
2. Initially, we had hoped to obtain separate average monthly benefit data for the Basic and UP programs, but ACF does not collect the data separately. For most quarters in the time series, quarterly data were available from ACF. When only monthly variables were available, quarterly data were computed by taking a weighted average of the AMB in each month of the quarter.
3. From 1980 through 1986, the second and fourth quarter values of the regional CPI are the average of the two bi-monthly values appearing in those quarters. For the first and third quarters, however, the value equals the one bi-monthly estimate in the quarter, February and August, respectively. From 1987 through 1995, is the average of the three monthly values in the given quarter.
4. We identify AFDC Basic units as those families or sub-families reporting having received AFDC benefits with a single reference person who has never been married, who is widowed, divorced, or separated, or whose spouse is absent. Based on conversations with individuals at ASPE, we also flag families headed by a married couples as AFDC Basic units if either parent has a disability or has held a job during the month in question. We classify all remaining families or sub-families receiving AFDC benefits as AFDC UP units.
5. Depending on the source for these initial rates, adjustments may also be made in order to obtain estimates that reflect average monthly caseloads.
6. We unsuccessfully attempted to produce state-level estimates of female headed households (FHHs). The plan required: 1) estimation of a nine-region pooled regression model for FHH using regional FHH estimates from the Current Population Survey (CPS) and vital statistics data aggregated to the regional level; 2) prediction of state values from the estimated model using state vital statistics data; and 3) controlling predicted state series to estimates from the 1980 and 1990 Censuses. However, these efforts failed to produce reliable estimates. The vital statistics variables proved to be very poor predictors of FHHs at the regional level. We attribute this to the erratic behavior of the FHH estimates over time within region. We expected that CPS-based FHH estimates at the regional level would be sufficiently reliable for our purpose, but this is apparently not so.
7. Monthly total unemployment by state were readily available from the BLS back to 1978. However, using this series would have limited the number of lags available for use in model. To obtain the maximum number of lags possible, we calculated and used the alternate total unemployment series described above. The correlation coefficient for the series available from the BLS and the calculated series was .93.
8. Although the value of MTBBR varies within a state over time, changes generally correspond to changes in federal requirements (OBRA-81 and DEFRA-84) and changes in the EITC. Thus, changes usually occur in the same quarter for most, if not all, states and are approximately equal across states. Overall, MTBBR follows a downward trend throughout the period.
9. A given family's maximum AFDC benefit may differ from the state's "typical" benefit as calculated by the ACF due to factors such as: locality, housing arrangements, family composition, or special needs.
10. More specifically, for each state we observed the quarter in which the nominal benefit changed after 1982. For most states, the quarter was the same every year, so we assumed that earlier changes were made in the same quarter in previous years. For states that did not follow a consistent pattern, with Florida being the most notable of these states, we assumed that changes before October 1982 occurred in the same quarter as the first change after October 1982. In addition, we cross-checked ACF data with semi-annual maximum monthly payment data from the Congressional Research Service. When a discrepancy appeared between the two series, an effort was made to explain the discrepancy and include the appropriate data.
11. We explored the use of effective benefit reduction rates estimated by Fraker, et al (1985) and McKinnish, et al (1995). Unfortunately, a series including all 50 states and the District of Columbia began in 1984 and only extended through 1991.
12. Technically, AFDC monthly benefits paid fall to zero as soon as the calculated benefit falls below $10; i.e., there is a notch in the disposable income schedule a few dollars below the earnings cut-off. Our measure smoothes over that notch.
13. The monthly standard allowance has varied over time as a result of federal legislation, in particular OBRA-81, DEFRA-84, and FSA-88.
14. A review of waivers implemented since 1991 appears in GAO (1996).
15. Merz, et al (1995) uses the term "therapeutic" for "medically necessary" and/or "elective" abortions.
16. The Appendix provides a more detailed explanation for the interpolation process used to create each quarterly series.
CHAPTER FIVE: REGRESSION RESULTS
A. INTRODUCTION
We present and discuss the regression results in this chapter. The participation equation results for the Basic program are in Section B, those for the Unemployed Parent program are in Section C, and the average monthly benefit results for the combined programs are in Section D. We consider the estimated effects for the labor market variables in more detail in Section E, including comparisons to findings from other studies. We do the same for the estimated AFDC program parameter effects in Section F.
B. BASIC PARTICIPATION EQUATIONS
1. Determining the Final Specifications
The results reported here were arrived at after trying many alternative specifications. The number of explanatory variables that could justifiably be included in any individual model is very large, especially when multiple lags for a single variable are included. While the number of "state-quarter" observations used (51 x 60 = 3,060) makes it technically possible to include a very large number of explanatory variables in a single equation, collinearity among explanatory variables (especially multiple lags of the same variable) would have made results from specifications with many more explanatory variables both imprecise and difficult to interpret. In addition, the software we used to implement the Parks method, SAS-ETS TSCSREG, limited us to using fewer explanatory variables than quarters in any one model (no more than 60).(1)
We conducted the specification search using the Basic caseload as the dependent variable. We first included explanatory variables that we thought most likely to be statistically significant, with a limited number of lags -- the expected participation variable, the unemployment rate, the program parameters, and a few others. We then expanded lag specifications for variables that proved to be significant, and tried alternative lags for ones that were not. Variables that had insignificant coefficients were dropped along the way, and new variables not included in the initial specification were added. We generally used absolute t-statistics in excess of 2.0 as evidence of statistical significance, but accepted a lower value when the coefficient had the anticipated sign and/or if the 2.0 standard was met in many, but not all, specifications.
As a result of the specification search, the t-statistics reported need to be interpreted cautiously. Many of the most important findings were very robust to specification changes, but others are less robust and some have not been tried in many variants. Note, in particular, that a large number of variables in the "other programs and laws" category were tried and only a few have been retained -- in some cases they have the wrong sign. In any specification search we would expect to find at least some variables with large t-statistics even if all of the "true" coefficients were zero. It is also possible that a different search strategy would have yielded a different set of explanatory variables in the final models.
The estimated effects of increases in the unemployment rate are especially robust across the many specifications tried, as well as across participation equations within each program and across estimation methodologies (Parks vs. Weighted Least Squares). The trade employment variable also had consistently strong coefficients in all specifications in which it was included, while other employment variables were consistently insignificant. For the Basic models, the maximum monthly benefit (MMB), average tax and benefit reduction rate (ATBR), and gross income limit (GIL) variable coefficients are all remarkably robust across equations, explanatory variable specifications, and estimation methodologies. UP results for these program variables were considerably weaker, but are consistent across specifications - especially for MMB. We tried many specifications of the vital statistics variables. We consistently found significant results for the out-of-wedlock births and marriage variables in the Basic equations. The divorce variable was not significant in any specification. Results for the Immigration Reform and Control Act variable in the Basic equations are consistently strong. Results for other explanatory variables were much less robust, as discussed further below.
Once we finished the specification search for the caseload equation, we estimated the total recipient and child recipient equations with the same set of explanatory variables. Coefficients proved to be very similar across participation equations, so we did not search further using the recipient dependent variables. We also estimated the same models for all three participation measures, but with the vital statistics variables omitted. As discussed previously, this was done to determine the extent to which the effect of business cycles on participation works through their effect on family characteristics.
We discuss the coefficients for the various sets of explanatory variables included in the final specification (Exhibit 5.1) below, and also discuss alternative specifications that were tried. Note that coefficients of explanatory variables that are in logarithms are elasticities -- percent change in the caseload (or other dependent variable) per one percent change in the explanatory variable (an elasticity of 0.5, for instance, means a one percent change in the explanatory variable is associated with a 0.5 percent change in the dependent variable). Coefficients of other variables can be interpreted as the percent change in the dependent variable per unit change in the explanatory variable after multiplying by 100. For dummy variables, the coefficient times 100 can be interpreted as the percent change in the dependent variable associated with a change from the "zero" category of the dummy to the "one" category. "Long-run" estimates that are reported for explanatory variables with multiple lags are sums of the coefficients over all lags and represent the effect of a permanent change in the variable after the number of quarters indicated by the maximum lag length.
Exhibit 5.1
| Regression Results for Basic Models | |||||||||||||
| Sample: 51 states, 1979.4 - 1994.3 | |||||||||||||
| Dependent Variable is change in ln(participation/expected participation)a | |||||||||||||
| Coefficients | T-statistics b | ||||||||||||
| Explanatory | Caseload | Recipients | Child Recipients | Caseload | Recipients | Child Recipients | |||||||
| Variablesc | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | |
| ln(unemployment rate) | 10xa0 | 0.250 | 0.256 | 0.261 | 0.268 | 0.222 | 0.225 | 9.4 | 11.1 | 8.9 | 10.1 | 8.5 | 9.8 |
| (PDL: L = 14) | 100xa1 | -0.343 | -0.370 | -0.477 | -0.489 | -0.334 | -0.343 | -3.7 | -4.7 | -4.5 | -5.1 | -3.9 | -4.5 |
| 1000xa2 | 0.148 | 0.167 | 0.257 | 0.264 | 0.154 | 0.161 | 2.4 | 3.1 | 3.5 | 4.0 | 2.6 | 3.1 | |
| long-run elasticity | 0.165 | 0.165 | 0.152 | 0.156 | 0.138 | 0.141 | |||||||
| ln(trade employment per cap.) | 10xa0 | -0.650 | -0.738 | -0.602 | -0.733 | -0.511 | -0.598 | -3.9 | -5.2 | -3.1 | -4.0 | -3.2 | -4.2 |
| (PDL: L = 10) | 100xa1 | -2.427 | -2.324 | -2.290 | -2.170 | -2.252 | -2.180 | -7.5 | -8.2 | -5.8 | -5.9 | -6.5 | -7.1 |
| 1000xa2 | 2.721 | 2.690 | 2.646 | 2.663 | 2.223 | 2.244 | 6.6 | 7.6 | 5.4 | 5.8 | 5.1 | 5.8 | |
| long-run elasticity | -1.002 | -1.054 | -0.903 | -0.974 | -0.944 | -0.993 | |||||||
| ln(maximum monthly benefit) | current | 0.080 | 0.082 | 0.075 | 0.077 | 0.098 | 0.097 | 4.5 | 5.5 | 4.1 | 4.6 | 6.4 | 7.3 |
| 1st lag | 0.151 | 0.151 | 0.129 | 0.131 | 0.136 | 0.138 | 8.1 | 9.7 | 6.8 | 7.4 | 8.1 | 9.3 | |
| 2nd lag | 0.039 | 0.040 | 0.012 | 0.014 | 0.020 | 0.021 | 2.2 | 2.6 | 0.7 | 0.9 | 1.3 | 1.6 | |
| long-run elasticity | 0.270 | 0.274 | 0.216 | 0.222 | 0.254 | 0.256 | |||||||
| average tax and | current | -0.033 | -0.038 | -0.030 | -0.033 | -0.030 | -0.031 | -2.3 | -3.2 | -2.4 | -2.7 | -2.5 | -2.9 |
| benefit reduction rate | 1st lag | -0.080 | -0.081 | -0.064 | -0.068 | -0.079 | -0.079 | -5.4 | -6.5 | -4.8 | -5.3 | -6.1 | -7.0 |
| 2nd lag | -0.041 | -0.041 | -0.016 | -0.019 | -0.035 | -0.038 | -2.8 | -3.4 | -1.2 | -1.5 | -2.8 | -3.4 | |
| long-run effect | -0.153 | -0.160 | -0.111 | -0.120 | -0.144 | -0.148 | |||||||
| AFDC earnings cut off | current | -0.051 | -0.052 | -0.048 | -0.048 | -0.055 | -0.055 | -8.8 | -10.2 | -7.7 | -8.1 | -10.1 | -11.1 |
| relative to gross income limit | 1st lag | -0.038 | -0.038 | -0.027 | -0.028 | -0.040 | -0.042 | -6.2 | -7.1 | -4.4 | -4.7 | -6.9 | -8.0 |
| 2nd lag | -0.011 | -0.009 | -0.004 | -0.004 | -0.014 | -0.015 | -1.9 | -1.8 | -0.6 | -0.7 | -2.6 | -3.1 | |
| long-run effect | -0.100 | -0.099 | -0.079 | -0.079 | -0.109 | -0.112 | |||||||
| OBRA81 | current | -0.039 | -0.037 | -0.025 | -0.026 | -0.033 | -0.033 | -5.3 | -6.2 | -3.2 | -3.6 | -4.9 | -5.5 |
| 1st lag | -0.020 | -0.021 | -0.002 | -0.002 | -0.022 | -0.021 | -2.5 | -3.1 | -0.2 | -0.3 | -3.0 | -3.3 | |
| 2nd lag | -0.010 | -0.012 | -0.022 | -0.022 | -0.010 | -0.008 | -1.4 | -1.9 | -3.0 | -3.3 | -1.4 | -1.4 | |
| long-run effect | -0.069 | -0.070 | -0.048 | -0.050 | -0.064 | -0.063 | |||||||
| DEFRA84 | current | -0.006 | -0.006 | -0.006 | -0.005 | -0.002 | -0.002 | -1.3 | -1.8 | -1.6 | -1.4 | -0.6 | -0.9 |
| Coefficients | T-statisticsb | ||||||||||||
| Explanatory | Caseload | Recipients | Child Recipients | Caseload | Recipients | Child Recipients | |||||||
| Variablesc | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | |
| family cap | 1st lag | -0.023 | -0.024 | -0.017 | -0.018 | -0.020 | -0.019 | -3.2 | -4.0 | -2.1 | -2.3 | -2.6 | -2.8 |
| IRCA immigrants per 100 | 1st lag | 0.050 | 0.044 | 0.023 | 0.020 | 0.036 | 0.034 | 5.0 | 5.6 | 1.5 | 1.5 | 4.8 | 5.3 |
| Medicaid expansiong | current | 0.179 | 0.190 | 0.058 | 0.045 | 0.160 | 0.153 | 2.5 | 2.9 | 0.8 | 0.6 | 2.9 | 3.1 |
| Med. exp. x share participatingg | current | -1.230 | -1.327 | -0.216 | -0.120 | -1.206 | -1.148 | -2.1 | -2.5 | -0.3 | -0.2 | -3.1 | -3.2 |
| ln(out-of-wedlock births)e | 0.101 | 0.111 | 0.073 | 3.8 | 3.3 | 3.0 | |||||||
| ln(marriages)e | -0.097 | -0.139 | -0.094 | -3.3 | -4.2 | -3.2 | |||||||
| ln(SSI child beneficiaries) | current | 0.009 | 0.009 | 0.007 | 0.007 | 0.009 | 0.009 | 2.3 | 2.7 | 1.5 | 1.8 | 2.6 | 2.9 |
| ln(% insured unemployed) | 1st lag | 0.013 | 0.014 | 0.009 | 0.009 | 0.008 | 0.008 | 3.7 | 4.3 | 2.2 | 2.5 | 2.0 | 2.5 |
| abortion: parental consent/notice | 1st lag | -0.002 | -0.002 | 0.000 | 0.001 | -0.003 | -0.003 | -1.0 | -1.6 | 0.3 | 0.4 | -2.2 | -2.5 |
| Medicaid restricted | 1st lag | -0.003 | -0.003 | 0.002 | 0.002 | -0.005 | -0.005 | -1.8 | -2.4 | 1.1 | 1.2 | -3.1 | -3.5 |
| SSDI initial allowance ratef | -0.053 | -0.046 | -0.072 | -0.071 | -0.157 | -0.153 | -2.1 | -2.0 | -2.6 | -2.9 | -5.5 | -5.9 | |
| 1979 dummies for: | Alaska | 0.018 | 0.005 | 0.053 | 0.056 | 0.183 | 0.176 | 0.1 | 0.0 | 0.3 | 0.3 | 0.9 | 1.0 |
| Hawaii | 0.060 | 0.041 | 0.074 | 0.048 | 0.191 | 0.175 | 0.7 | 0.5 | 0.8 | 0.5 | 2.3 | 2.4 | |
| D.C. | -0.057 | -0.059 | -0.013 | -0.011 | 0.017 | 0.008 | -1.3 | -1.5 | -0.3 | -0.2 | 0.4 | 0.2 | |
| Seasonal Dummies | Spring | -0.004 | -0.002 | -0.004 | -0.002 | -0.006 | -0.006 | -0.6 | -0.4 | -0.6 | -0.3 | -1.4 | -1.4 |
| Summer | -0.010 | -0.007 | -0.008 | -0.005 | -0.013 | -0.013 | -1.4 | -1.2 | -1.1 | -0.7 | -2.1 | -2.3 | |
| Fall | 0.053 | 0.054 | 0.046 | 0.046 | 0.040 | 0.041 | 7.1 | 8.9 | 5.8 | 6.2 | 6.5 | 7.4 | |
| Calendar Year Dummies | 1979 | 0.010 | 0.021 | 0.006 | 0.014 | -0.012 | -0.005 | 0.6 | 1.5 | 0.4 | 1.1 | -0.9 | -0.4 |
| 1980 | 0.009 | 0.014 | -0.007 | -0.002 | 0.016 | 0.021 | 0.8 | 1.4 | -0.6 | -0.2 | 1.8 | 2.7 | |
| 1981 | -0.040 | -0.039 | -0.061 | -0.059 | -0.033 | -0.032 | -2.9 | -3.3 | -5.0 | -5.0 | -3.1 | -3.6 | |
| 1982 | -0.022 | -0.019 | -0.006 | -0.003 | -0.016 | -0.016 | -1.9 | -1.8 | -0.5 | -0.3 | -1.7 | -2.1 | |
| 1983 | 0.004 | 0.007 | 0.013 | 0.018 | 0.016 | 0.019 | 0.3 | 0.7 | 1.4 | 2.0 | 2.0 | 2.7 | |
| 1984 | 0.004 | 0.011 | 0.027 | 0.033 | 0.024 | 0.030 | 0.3 | 1.1 | 2.8 | 3.6 | 2.9 | 4.5 | |
| 1985 | 0.034 | 0.044 | 0.028 | 0.041 | 0.042 | 0.051 | 3.1 | 4.8 | 2.7 | 4.3 | 4.9 | 7.2 | |
| 1986 | 0.034 | 0.039 | 0.024 | 0.032 | 0.031 | 0.037 | 3.2 | 4.3 | 2.5 | 3.4 | 3.7 | 5.3 | |
| 1987 | 0.016 | 0.021 | 0.010 | 0.018 | 0.021 | 0.028 | 1.5 | 2.4 | 1.1 | 2.1 | 2.6 | 4.2 | |
| 1988 | 0.031 | 0.037 | 0.022 | 0.028 | 0.030 | 0.035 | 2.9 | 4.1 | 2.4 | 3.1 | 3.7 | 5.3 | |
| 1989 | 0.042 | 0.048 | 0.038 | 0.047 | 0.040 | 0.048 | 3.7 | 5.2 | 4.0 | 5.0 | 4.5 | 6.5 | |
| 1990 | 0.048 | 0.055 | 0.047 | 0.055 | 0.059 | 0.063 | 4.5 | 6.1 | 4.7 | 5.7 | 7.0 | 9.0 | |
| 1991 | 0.038 | 0.045 | 0.034 | 0.042 | 0.032 | 0.038 | 3.5 | 5.1 | 3.5 | 4.5 | 4.0 | 5.7 | |
| 1992 | 0.005 | 0.005 | -0.004 | -0.003 | -0.006 | -0.003 | 0.4 | 0.5 | -0.5 | -0.3 | -0.7 | -0.5 | |
| 1993 | -0.006 | -0.003 | -0.022 | -0.019 | -0.016 | -0.013 | -0.6 | -0.3 | -2.4 | -2.0 | -1.9 | -2.0 | |
| 1994 | -0.018 | -0.016 | -0.022 | -0.021 | -0.013 | -0.011 | -1.1 | -1.2 | -1.7 | -1.6 | -1.1 | -1.2 | |
a Expected participation variable is based on national age-specific participation rates for 1990 and estimated population of the state by age in the quarter.
b T-statistics in bold are at least 2.0 in absolute value. These statistics were reduced from those calculated by SAS to make a correction for degrees of freedom that is not made by the procedure used (TSCSREG). The reduction factor used is .41, computed as [(T - K)/T].5, where T is the number of quarters (60) and K is the number of explanatory variables (50).
c All explanatory variables except quarter and year dummies are changes. Quarter and year dummies are equal to .25 in the quarters/years indicated so that coefficients can be interpreted as annualized rates of growth. For the polynomial distributed lag (PDL) variables, the coefficient of the variable lagged j periods is a0 + a1 j + a2 j2 for j = 0, 1, 2, ... L. Other variables are lagged the number of periods indicated.
d Indicates whether vital statistics variables are included (with v.s.) or not (without v.s.). The vital statistics variables are ln(out-of-wedlock births) and ln(marriages).
e Variables are moving averages of previous four quarters.
f This variable is the change in the state's SSDI initial allowance rate from 1977 to 1978 times the 1979 year dummy. Special dummies for three states were included due to missing initial allowance data.
g "Medicaid expansion" is the share of children in the state covered under the Medicaid expansions that began in 1988. "Share participating" is the share of children in the state who were in AFDC families in the year before the expansions began (1987 -- average monthly child recipients divided by population under 19).
The results we focus on below were estimated using the Parks method (Chapter 3). At the end of this section we compare the caseload results from the Parks method to estimates of the same model using a weighted least squares (WLS) method, with weights proportional to population size.
2. Year and Seasonal Effects
2. Year and Seasonal Effects
The estimated coefficients of the seasonal and calendar year dummies appear at the end of Exhibit 5.1. Recall that the calendar year dummies can be interpreted as the annualized growth rate in the first (winter) quarter holding all other variables constant. To obtain the annualized growth rate for the full year holding all other variables constant it is necessary to add the average of the seasonal coefficients (including zero for the winter quarter) to the calendar year coefficient. For the basic caseload equation, the average of the seasonal coefficients is 1.0 percent, i.e., .010 = (0 - 0.004 - 0.010 + 0.053 )/4. In interpreting these coefficients, it should be kept in mind that they may be misleading with respect to the extent of national participation growth not accounted for by the state variables because the state observations were not weighted by relative size in estimating the model. The simulations reported later (Chapter 6) do so. Nonetheless, the patterns of the year coefficients are closely related to the patterns of national growth not accounted for that are found in the simulations.
All but three of the calendar year coefficients are positive in the caseload equation with vital statistics after the seasonal adjustment. The positive values for each year from 1985 to 1991 are significant and substantial. This indicates that substantial growth in the caseload during this period is not accounted for by the variables in the model. The largest calendar year coefficient is 4.8 in 1990; after adjusting for seasonal effects, the estimate implies that the caseload grew by 5.8 percent in that year for reasons not accounted for by other variables in the model. The smallest coefficient is for 1981, the year that OBRA81 was implemented: -3.0 percent after adjustment. This represents only a portion of the possible effect of OBRA81, as we discuss further below. In all other years (1979-80, 1982-84, and 1992-94) the calendar year dummies are under 1.0 percent in absolute value after adjustment, and not statistically significant. Results are similar in other equations.
In summary, the state-level factors in the model appear to account for most of the growth in the caseload in eight of the 16 years of the sample period. For the seven years from 1985 to 1991, substantial growth is not accounted for by these variables, and these variables do not account for some of the decline in participation in 1981. As will be demonstrated by the simulations (Chapter 6), the state-level factors do explain much of the large cyclical variation in the caseload, but leave much of the long-term trend in the caseload unaccounted for.
3. Demographic Variables
Population Growth and Aging
The expected participation variables allow us to capture the effects of both growth and aging of the at-risk population in a single variable. They do not, however, appear explicitly as explanatory variables in Exhibit 5.1. They are included, but their coefficients are fixed. As discussed in Chapter Three, we hypothesized that the true coefficients of the expected participation variables are each one (a one percent increase in expected participation due to population growth and aging leads to a one percent increase in actual participation). The expected participation variable was, by far, the most significant variable in the initial specifications. The coefficients were always less than one, but not often significantly less than one. Hence, we imposed the restriction that the coefficient is one. This is equivalent to using the logarithm of actual relative to expected participation as the dependent variable, as we report at the top of the exhibit.
Vital Statistics
Of the three vital statistics variables, out-of-wedlock births, marriages, and divorces, only the first two were significant in most specifications tried, for at least some lags. Coefficients of the divorce variable generally had the wrong sign and were, at best, marginally significant. We suspect that reported divorces are a poor predictor of participation because AFDC participation may begin in anticipation of divorce in many cases. Hence, we dropped the divorce variable from the final specification.(2)
The coefficients of the vital statistics variables are quite significant. Both a one percent increase in out-of-wedlock births and a one percent reduction in marriage are associated with a 0.1 percent increase in participation.(3)
Immigration
Two immigration variables were tried, the number of immigrants legalized under IRCA-86, and the number of other legal immigrants -- both as immigrants per capita, and both in level, rather than change, form.(4) The former variable consistently had a statistically significant coefficient, and the latter never did. Waiting periods on AFDC participation for IRCA immigrants (five years) and others (three years) during this period make it unlikely that the immigrants themselves would become participants as soon as one year after immigration.
One possible reason for the significant coefficient on the IRCA variable is the "child-only" phenomenon that has been observed in California and other states with large numbers of IRCA immigrants. Many parents legalized under IRCA had children who were citizens because they had been born in the United States. These children were eligible for benefits prior to their parents' legalization, but parents evidently feared deportation should they apply. Once the parents became legal immigrants, many applied for benefits for their children. The estimates imply that each legalization per 100 population resulted in a 5.0 percent increase in the caseload. The coefficient in the child recipient equation is smaller, 3.6 percent, suggesting that the number of child recipients in these families is smaller than for the mean AFDC Basic family. The coefficient in the total recipient equation is smaller still, 2.3 percent, consistent with the "child-only" explanation.
4. Labor Market Variables
As mentioned above, the final specifications include a quadratic distributed lag in the change in the log of (age-adjusted) unemployment. We found that as many as 14 lags of the unemployment rate could be included in the models without obtaining a negative coefficient, with almost all coefficients statistically significant. This was surprising because previous studies using quarterly data had used no more than five lags. After discovering this, we imposed polynomial distributed lags (DLs) on the unemployment rate coefficients to smooth them and to conserve on the number of explanatory variables. A quadratic DL is used in the final specification.(5) Three explanatory variables that are functions of the current and 14 lagged values of the change in the log of unemployment appear in the model, each corresponding to one of the parameters of the quadratic function.(6) We also used polynomial DLs for other unemployment or employment variables that were tried. The models reported include quadratic DLs for the change in the log of trade employment per capita.
We also include a quadratic distributed lag in the current and first 10 lags of the log of trade employment per capita. Other labor market variables tried with distributed lags are unemployment per capita, employment per capita, and manufacturing employment per capita. None of these alone exhibited more explanatory power (i.e., results in lower mean square error) for the caseload equation than the unemployment rate variable alone, and the only variable that adds substantial explanatory power when the unemployment rate variable is included is trade employment per capita. We also experimented with several lags of average weekly earnings in trade and in manufacturing. Trade earnings are not significant, and manufacturing earnings are marginally significant, with the expected negative sign, but only in specifications without trade employment.
The effect of business cycles is jointly captured by the unemployment rate and trade employment variables in these models. The estimated long-run elasticity for the unemployment rate -- the effect of a permanent one-percent increase in the unemployment rate on the caseload after 14 quarters, in percent -- is the sum of the 15 implied coefficients on the current and 14 lags of the unemployment rate variable. The sum is 0.165; i.e., a one percent increase in unemployment eventually leads to an 0.165 percent increase in the caseload. This is not as small as it first appears, as is evident in the following illustration. A one percentage point increase in the unemployment rate from 5 percent to 6 percent is a 20 percent increase, and applying the long-run elasticity of 0.165 to 20 percent yields an increase in the caseload of over three percent.(7) The increase in the national unemployment rate associated with the most recent recession was more than twice as large as the hypothetical one percentage point increase of our illustration: 2.4 percentage points.(8)
The reported long-run unemployment elasticity alone substantially understates the possible effect of a recession on the Basic caseload because it does not include estimated effects that work through the trade employment variable. When the trade employment variable is not included in the caseload equation, the long-run unemployment rate elasticity is substantially higher, 0.313. Using this figure, the hypothetical one percentage point increase in the unemployment rate described above results in a 5.7 percent increase in the caseload after 14 quarters.(9)
The long-run unemployment elasticities in the recipient and child recipient equations are somewhat smaller, indicating that families induced to obtain welfare benefits by a recession have fewer children than the average AFDC family.
The estimated long-run elasticity for trade employment per capita is -1.00; i.e., a permanent one percent increase in trade employment reduces the caseload by one percent. The corresponding values in the recipient and child recipient equations are slightly smaller, but all above 0.90 in absolute value. It would probably be a mistake to conclude that increasing employment in trade, specifically, would substantially reduce the caseload. The estimated elasticity likely reflects the effects of business cycles, and captures a feature of business cycles that is particularly important to potential AFDC families. The full estimated effects of changes in the unemployment rate and trade employment variables during business cycles are illustrated in the simulations presented in the next chapter.
Dropping the vital statistics variables from the specification increases the magnitude of the long-run elasticities for the two labor market variables, as expected, but only slightly. There are also minor increases in the magnitudes of the AFDC program parameter coefficients. These results suggest that very little of the impact of recessions or of changes in program parameters works through changes in family characteristics; alternatively, we may have missed a more substantial effect because the vital statistics variables are inadequate proxies for family characteristics.
Further discussion of the estimated employment effects appears in Section E, below.
5. AFDC Program Variables
Program Parameters
We used four program parameters in some early specifications of the model: the maximum monthly benefit (MMB), the marginal tax and benefit reduction rate (MTBRR), the average tax and benefit reduction rate (ATBRR), and the AFDC earnings cut off (ECO) relative to the gross income limit (GIL). The MTBRR coefficient was never significant, even marginally, which we attribute to relatively little variation in changes across states in any given year during the sample period. Coefficients of the current and first lag of the other three parameters were very significant in virtually all specifications tried, and the second lag of each was sometimes as significant as well. Hence, the current and first two lags of each of MMB, ATBRR and the ratio of the ECO to the GIL are included in the specifications reported.
The estimated effects of increases in the MMB, the ATBRR, and the ratio of the ECO to the GIL are all statistically significant and consistent in sign with the predictions of the static participation model (Chapter 1). We estimate that a one-percent increase in the MMB increases the caseload by about 0.27 percent after two quarters. An increase in the ATBRR of 10 percentage points (e.g., 70 percent to 80 percent ) is estimated to reduce the caseload by about 1.5 percent after two quarters as some families receiving small benefits because of earnings or other income leave the caseload. An increase in the ratio of the ECO to the GIL of 10 percentage points is estimated to reduce the caseload by 1.0 percent. Estimated effects on recipients and child recipients are quite similar. We discuss the results for the program parameters further in Section F, below.
Federal Legislation
The only dummies for federal legislation that have statistically significant coefficients in any models are the OBRA81 and DEFRA84 dummies. The current and first two lags of the OBRA81 dummy are significant (the last only marginally so). It should be noted that the dummy coefficients do not capture the full effect of OBRA81. OBRA81 increased the ATBRR in most states and also introduced the GIL. The effects of these specific OBRA81 changes are presumably captured by the program parameter variables themselves. Further, the dummy variables for calendar years 1981 and 1982 imply annual caseload reductions of about 3.0 (i.e., -0.03 = -0.04 + (0 - 0.004 - 0.010 + 0.053)/4) and 1.2 percent, respectively, after controlling for other factors and adjusting for seasonal effects, which might also be attributable to OBRA81. The full estimated effects of OBRA81 on the Basic caseload are more apparent in the simulations (Chapter 6).
The coefficient for the DEFRA84 dummy lagged one period is negative, but not significant in the equations reported; it was negative and significant in many specifications we tried. Other lags had much smaller coefficients. We expected this coefficient to be positive if significant, because DEFRA84 partially reversed the changes of OBRA81. The full estimated effect of DEFRA84 includes the effects of resulting changes in program parameters, including the increase in the GIL from 150 percent of the state's need standard to 185 percent. Further, the calendar year coefficients in the caseload equation indicate a 1.4 percent unexplained increase in the caseload in 1984 (after adjusting for seasonality, i.e., 0.014 = 0.004 + (0 - 0.004 - 0.010 + 0.053)/4), and a 4.4 percent increase in the following year, which might at least partly be attributable to implementation of DEFRA84. It may also be that coefficients for other federal legislation dummies (for OBRA87, the provisions of FSA88, OBRA90, and OBRA93) are insignificant because the effects of the legislation are captured by the program parameters and the year dummies. These changes are one of several possible explanations of the substantial caseload growth not accounted for by state-level variables from 1985 to 1991.
We were somewhat surprised to find that the federally mandated introduction of UP programs in 1990 in states without existing UP programs did not have an identifiable impact on the Basic caseload. We had expected to find some shift from the Basic caseload to the UP caseload in these states, especially those with 12 month programs, but did not find any statistically significant shift.
1115 Waivers
Only one of the 1115 waiver dummies we tried had a statistically significant coefficient, the "family cap" dummy for restrictions on benefits for children born while the mother is an AFDC recipient. According to the estimate, such restrictions reduce the caseload by 2.3 percent after one quarter, but have no further effect. We did not expect such restrictions to have an impact on caseloads, at least so quickly. The most likely effect would be a reduction in child recipients, and perhaps only after several quarters (allowing nine months for gestation). The estimated effect on child recipients, however, is slightly smaller than the effect on the caseload.
While it could be that some one-parent families are deterred from welfare dependency by such restrictions, there are three more likely explanations. First, it may be that this waiver dummy is proxying for other administrative efforts in the waiver states to reduce caseloads. The three states that instituted family caps during the sample period are New Jersey (1992.4), Georgia (1994.1), and Wisconsin (1994.3), and the family caps are part of broader efforts to reduce welfare dependency in each state. Second, some AFDC families who have children subject to the cap may have migrated to other states without caps. Third, the finding may be due to random error; given the number of other variables we tried, it would be surprising if we didn't include at least one or two that really were not important in our final specification.
We had not expected to find strong effects for the waivers because each is implemented in only a small number of states and only for a short period before the end of the sample period. Hence, it would be premature to conclude that the requirements implemented under the waivers have little effect on caseloads or recipients.
6. Other Programs and Laws
Very few of the variables in the category of new programs and laws had statistically significant coefficients in the specifications we tried, and the signs of several of these coefficients are opposite that expected. In contrast to the several strong findings for some of the demographic, labor market, and program variables reported above, none of the findings reported below stand out as particularly strong or convincing. It is important to keep in mind that they are a product of a specification search over many variables.
Medicaid
The final specification of the Basic participation models includes two Medicaid variables. "Medicaid expansion" is the share of children under 19 in the state eligible for Medicaid under the Medicaid expansions that began in 1988. The variable is zero before 1988. The second variable is the Medicaid expansion variable multiplied by the share of children under 19 in the state who were AFDC recipients in 1987 (average monthly child recipients), the pre-expansion year. Both variables are entered as changes in the current quarter.
We expected the Medicaid expansion variable when included alone to have a negative coefficient, especially given the strong findings reported by Yelowitz (1994) from his analysis of the same expansions using CPS data for individuals linked to state eligibility and expenditure data.(10) Instead, however, we found a marginally significant, positive coefficient. We added the interaction term on the hypothesis that the expansion would have a larger negative effect (or smaller positive effect) in states in which a large share of children were already on AFDC and, therefore, covered by Medicaid. The coefficient of the interaction variable is consistent with this hypothesis. In fact, the combined coefficients imply that the estimated effect of the expansion is positive in states where the share of children on AFDC in 1987 is below 14.6 percent, and negative in states where the share is larger.(11) Most states are in the former category, but a few are in the latter -- including California (15.9 percent).
One other notable feature of the findings is that it is only the current value of the variables that is statistically significant. We expected some lag in the effects of the expansions, but found that lagged values of the expansion variables did not have significant effects even when the current values were omitted from the equation.
One hypothesis about why the estimated effect of the expansion is positive for most states is that efforts to enroll newly eligible individuals into Medicaid also encouraged enrollment in AFDC. This does not explain, however, why the findings are at odds with those of Yelowtiz.
We also estimated models including a measure of the value of Medicaid benefits as an explanatory variables, but never found this variable to be statistically significant.
SSI children
The coefficient of the log of current SSI child beneficiaries is positive in all participation equations and significant in most. We were unsure about inclusion of this variable; on the one hand, it might capture the effects of shifts in AFDC children onto SSI after Sullivan v. Zebley, implying a negative coefficient, but on the other hand it might proxy for unobserved factors affecting participation in both programs in the same direction, which would imply a positive coefficient.
Unemployment Insurance
The log of the percent of unemployed persons who are insured has statistically significant, positive coefficients in all equations. As with the SSI child variable, there are conflicting sign expectations: increases in the share of insured unemployed should reduce the share of unemployed persons who meet the AFDC means test, suggesting a negative coefficient, but the variable might also proxy for unobserved factors that have the same effect on both the share insured and AFDC caseloads.
Abortion Restrictions
Two abortion dummies are included in the reported models (parental notification or consent requirements, and Medicaid funding restrictions), both lagged one period. The coefficient on the dummy for restrictions on Medicaid payments for abortions was more consistently significant than that on the parental consent/notification dummy. Both are negative, suggesting that the negative hypothesized effect of such restrictions on conceptions exceeds the positive effect on births for babies already conceived. The estimated coefficients imply that parental notification or consent requirements reduce caseloads by 0.2 percent and Medicaid funding restrictions reduce them by 0.3 percent. The estimated effects on the number of child recipients are larger -- reductions of 0.3 and 0.5 percent, respectively -- presumably because fertility reductions occur among AFDC mothers as well as potential AFDC mothers.
As with the findings for the family cap, these estimates are surprisingly strong, especially because the estimated effects occur after just two quarters. It may be that these effects are due to other efforts in the states that adopted these restrictions to reduce fertility and AFDC participation.
SSA Allowance Rates
Another variable in this category with a significant coefficient is our measure of SSA's administrative tightening of initial allowances from 1977 to 1978. According to our estimate, reductions in the allowance rate during this period resulted in increases in AFDC participation in 1979. This finding would be substantially strengthened if the sample period was extended back through 1978 and a strong effect were found in that year as well.
General Assistance
The final variable in this category is the measure we developed for cuts in state general assistance (GA) programs. Given the strong findings we obtained for the impact of these cuts on SSI participation in earlier research, we had expected to find some effect for AFDC even though the connection between AFDC and GA is more tenuous than that between SSI and GA. The coefficient of this variable, including lagged values, was not significant in any of the equations we tried. Given the size of the cuts that occurred and the success we had in using this variable in SSI models, we conclude that the GA cuts during this period had at most very small impacts on AFDC participation. States that cut their GA benefits may have been successful in assuring that AFDC-eligible families who sought GA, which is financed entirely from state and local revenues, obtained AFDC benefits, which are partially funded by the federal government, even before the GA cuts occurred. From our earlier work, it appears that the effect of the GA cuts on SSI applications and awards was high because the effort required to apply and the uncertain result discouraged them GA recipients from applying earlier. AFDC eligibility is easier to determine than SSI eligibility and, consequently, the determination process is much simpler. It might also be that those states which cut their GA programs also tightened their AFDC eligibility requirements or screens.
7. Weighted Least Squares Results
We conclude this section with a comparison of the Basic caseload results from the Parks method (Column 1 of both Exhibits 5.1 and 5.2), to estimates of the same model using a weighted least squares (WLS) method, with weights proportional to population size (Column 2 of Exhibit 5.3). Given the Parks specification, the latter method is presumably less efficient (higher standard errors) than the former. If the model specification is correct, both methods produce unbiased estimates. If the correct specification varies across states in a manner not captured by the specified model, then the coefficients could be substantially different. In that case the WLS coefficients would more accurately reflect the national caseload experience.
In general, the results from the two methods are very comparable. The long-run unemployment elasticity is 25 percent lower in the WLS results, but the trade employment elasticity is 13 percent higher. The MMB elasticity is slightly higher, and the ATBRR elasticity is almost unchanged. The change in the coefficient of the ratio of the ECO to the GIL is more substantial; it drops to about 60 percent of the value from the Parks model. The family cap coefficient changes very little. The IRCA immigrant coefficient increases somewhat, but the standard error is much larger so the t-statistic falls. The coefficients of the Medicaid expansion variable and its interaction with the share of children participating in AFDC both increase substantially in magnitude, as do their t-statistics, but these are offsetting changes when considering the actual effect on a specific state; the effect is negative if the share of children participating in AFDC is greater than 14.3 percent, compared to 14.6 in the Parks results. The magnitudes of the coefficients on both vital statistics variables are substantially reduced and no longer significant. The coefficients of the SSI child beneficiary variable, the percent insured unemployed variable, and the two abortion variables change very little. The coefficient of the SSDI initial allowance rate changes sign, however, and is essentially zero.
Exhibit 5.2
| Comparison of Basic Caseload Results | |||
| under Alternative Estimation Methodologies | |||
| Dependent Variable is change in ln(participation/expected participation) a | |||
| 51 states, 1979.4 - 1994.3 | |||
| Explanatory | Parks | Weighted | |
| Variablesb | Model | Least Squares | |
| ln(unemployment rate) | 10xa0 | 0.250 | 0.119 |
| (PDL: L = 14) | (9.35) | (4.30) | |
| 100xa1 | -0.343 | -0.054 | |
| (-3.73) | (-1.77) | ||
| 1000xa2 | 0.148 | 0.002 | |
| (2.36) | (1.01) | ||
| long-run elasticity | 0.165 | 0.123 | |
| ln(trade employment per cap.) | 10xa0 | -0.650 | -2.035 |
| (PDL: L = 10) | (-3.88) | (-8.62) | |
| 100xa1 | -2.427 | 4.278 | |
| (-7.46) | (4.26) | ||
| 1000xa2 | 2.721 | -3.232 | |
| (6.62) | (-3.59) | ||
| long-run elasticity | -1.002 | -1.129 | |
| ln(maximum monthly benefit) | current | 0.080 | 0.098 |
| (4.49) | (5.50) | ||
| 1st lag | 0.151 | 0.175 | |
| (8.15) | (8.81) | ||
| 2nd lag | 0.039 | 0.029 | |
| (2.16) | (1.66) | ||
| long-run elasticity | 0.270 | 0.302 | |
| average tax and | current | -0.033 | -0.019 |
| benefit reduction rate | (-2.35) | (-1.36) | |
| 1st lag | -0.080 | -0.082 | |
| (-5.45) | (-5.53) | ||
| 2nd lag | -0.041 | -0.050 | |
| (-2.83) | (-3.78) | ||
| long-run effect | -0.153 | -0.151 | |
| AFDC earnings cut off | current | -0.051 | -0.036 |
| relative to gross income limit | (-8.84) | (-5.12) | |
| 1st lag | -0.038 | -0.018 | |
| (-6.22) | (-2.52) | ||
| 2nd lag | -0.011 | -0.002 | |
| (-1.85) | (-0.33) | ||
| long-run effect | -0.100 | -0.057 | |
| OBRA81 | current | -0.039 | -0.041 |
| (-5.29) | (-6.54) | ||
| 1st lag | -0.02 | -0.030 | |
| (-2.54) | (-4.43) | ||
| 2nd lag | -0.01 | -0.011 | |
| (-1.39) | (-1.76) | ||
| long-run effect | -0.069 | -0.082 | |
| DEFRA84 | current | -0.006 | -0.005 |
| (-1.29) | (-2.10) | ||
| family cap | 1st lag | -0.023 | -0.021 |
| (-3.21) | (-2.89) | ||
| IRCA immigrants per 100c | 1st lag | 0.05 | 0.073 |
| (5.04) | (1.77) | ||
| Medicaid expansione | current | 0.179 | 0.475 |
| (2.46) | (5.99) | ||
| Med. exp. x share participatinge | current | -1.23 | -3.324 |
| (-2.06) | (-5.56) | ||
| ln(out-of-wedlock births)c | .101 | 0.053 | |
| (3.84) | (1.60) | ||
| ln(marriages)c | -0.097 | -0.017 | |
| (-3.35) | (-0.51) | ||
| ln(SSI child beneficiaries) | current | 0.009 | 0.011 |
| (2.31) | (2.26) | ||
| ln(% insured unemployed) | 1st lag | 0.013 | 0.011 |
| (3.67) | (2.50) | ||
| abortion: parental consent/notice | 1st lag | -0.002 | 0.002 |
| (-0.99) | (1.08) | ||
| Medicaid restricted | 1st lag | -0.003 | -0.002 |
| (-1.79) | (-1.06) | ||
| SSDI initial allowance rated | -0.053 | 0.001 | |
| (-2.08) | (0.03) | ||
| 1979 dummies for: | Alaska | 0.018 | 0.040 |
| (0.11) | (0.27) | ||
| Hawaii | 0.06 | -0.005 | |
| (0.68) | (-0.07) | ||
| D.C. | -0.057 | -0.060 | |
| (-1.33) | (-1.35) | ||
| Seasonal Dummies | Spring | -0.004 | -1.00E-04 |
| (-1.36) | (-0.02) | ||
| Summer | -0.01 | -0.003 | |
| (7.10) | (-0.57) | ||
| Fall | 0.053 | 0.045 | |
| (0.64) | (8.83) |
| Calendar Year Dummies | 1979 | 0.01 | 0.075 |
| (0.64) | (5.29) | ||
| 1980 | 0.009 | 0.059 | |
| (0.78) | (5.84) | ||
| 1981 | -0.04 | -0.002 | |
| (-2.88) | (-0.18) | ||
| 1982 | -0.022 | -0.018 | |
| (-1.86) | (-2.15) | ||
| 1983 | 0.004 | -0.005 | |
| (0.35) | (-0.70) | ||
| 1984 | 0.004 | 0.001 | |
| (0.35) | (0.10) | ||
| 1985 | 0.034 | 0.034 | |
| (3.07) | (4.48) | ||
| 1986 | 0.034 | 0.036 | |
| (3.22) | (5.24) | ||
| 1987 | 0.016 | 0.014 | |
| (1.53) | (2.13) | ||
| 1988 | 0.031 | 0.032 | |
| (2.89) | (4.84) | ||
| 1989 | 0.042 | 0.043 | |
| (3.75) | (5.89) | ||
| 1990 | 0.048 | 0.058 | |
| (4.50) | (8.18) | ||
| 1991 | 0.038 | 0.043 | |
| (3.50) | (6.22) | ||
| 1992 | 0.005 | 0.019 | |
| (0.45) | (2.82) | ||
| 1993 | -0.006 | 0.001 | |
| (-0.56) | (0.21) | ||
| 1994 | -0.018 | -0.018 | |
| (-1.15) | (-2.26) | ||
| Autocorrelation coefficient | 1st Lag | f | 0.345 |
| (19.76) |
Numbers in parentheses are t-statistics.
a Expected participation variable is based on national age-specific participation rates for 1990 and estimated population of the state by age in the quarter.
b. All explanatory variables except quarter and year dummies are changes. Quarter and year dummies are equal to .25 in the quarters/years indicated so that coefficients can be interpreted as annualized rates of growth. For the polynomial distributed lag (PDL) variables, the coefficient of the variable lagged j periods is a0 + a1 j + a2 j2 for j = 0, 1, 2, ... L. Other variables are lagged the number of periods indicated.
c Variables are moving averages of previous four quarters.
d. This variable is the change in the state's SSDI initial allowance rate from 1977 to 1978 times the 1979 year dummy. Special dummies for three states were included due to missing initial allowance data.
e. "Medicaid expansion" is the share of children in the state covered under the Medicaid expansions that began in 1988. "Share participating" is the share of children in the state who were in AFDC families in the year before the expansions began (1987 -- average monthly child recipients divided by population under 19).
f. Autocorrelation coefficients vary across states in this specification.
Except in the first three years of the sample, the year coefficients change little. The two exceptions are for the first two years, in which they are much larger in the WLS results. We do not understand the reason for the changes in the initial years. Note, however, that the first two of these years are the only two that provide information about the effect of the SSDI allowance rate change, so the change in the year coefficients may be related to the change in the SSDI coefficient.
C. UNEMPLOYED PARENT PARTICIPATION EQUATIONS
1. Determining the Final Specifications
We present two sets of estimates for the UP participation models. In the first set -- the "full-period" estimates -- we use data for only the 19 states that have data for the whole sample period -- a total of 19 x 60 = 1,140 observations. In the second set -- the "post-mandate" estimates -- we use data for 49 states for the last 16 quarters of the sample period, during which all states were required to have UP programs -- a total of 784 observations. The District of Columbia, which had an UP program for the entire period, is excluded from both samples due to questionable data for the dependent variable in two quarters. Mississippi is excluded from the post-mandate sample for a similar reason.(12) For the latter sample we only estimate a caseload model.
As with the Basic program, we searched through many specifications for the full-period models prior to the specification reported here. The search was conducted in parallel with the search for the Basic equations, for the caseload equation only. In general, we searched in the same way as for the Basic equations, except that we elected to retain the same program parameter specification as in the Basic equation for comparison purposes.
We focused our search efforts on the labor market variables because prior research has demonstrated that these variables are more important for the UP program than for the Basic program. Nonetheless, we settled on the same two variables, the unemployment rate and trade employment per capita, for the final specification. The only difference between the specification of these variables in the Basic and UP equations is that the distributed lag for trade employment in the UP equation is first-order (linear) instead of second (quadratic), and the maximum lag length is six instead of ten.
For the post-mandate estimates, we started with the final specification from the full-period estimates, minus the dummies for the early years. We subsequently changed the specification in a few respects, as discussed later, but the two models are very similar in specification. We could not use the Parks method to estimate this model because the sample period is too short, so we applied only the WLS method. We discuss the findings for the full-period model first, then present the post-mandate estimates.
2. Year and Seasonal Effects
The estimated coefficients of the seasonal and calendar year dummies appear at the end of Exhibit 5.3. Seasonal variation in participation is much greater for the UP program than for the Basic program. As in the Basic models, conversion of the calendar year dummy coefficients to obtain annual growth not accounted for by the model's other variables is done by adding the mean of the four seasonal coefficients (zero for the first quarter) to each calendar year coefficient. This mean is -17.4 percent, i.e., -0.174 = ( 0 - 0.218 - 0.340 - 0.130)/4.
All of the calendar year coefficients are positive in the caseload equation after adjusting for the seasonal factor except five (1982, and 1991 through 1994). In all other years the adjusted coefficients are substantial positive numbers, indicating that significant growth in the caseload during this period is not accounted for by the variables in the model. The largest coefficient is for the first year, 1979, followed by the second largest in 1980 and the third largest in 1981; after adjustment these are 0.40, 0.31, and 0.24. The largest coefficient in any other year is for 1988, 0.11 after adjustment. The simulations presented later (Chapter 6) show a similar pattern of growth not accounted for, but at substantially lower levels. The difference is evidently because the model accounts for a larger share of growth in relatively large states, and these get more weight in the decomposition analysis.
3. Demographic Variables
Expected Participation
As in the Basic equation, the expected participation variable's coefficient was the most significant coefficient in early runs, and we could not usually reject the hypothesis that the coefficient is one. Hence, we again constrained the coefficient to be one by incorporating it in the dependent variable.
Vital Statistics
The coefficients of the vital statistics variable were not significant in the specifications we tried. Theory would suggest that the signs of these coefficients would, if anything, be opposite those found in the Basic equation. Given this, the small size of the program, and the smaller sample size, the lack of a significant finding is not surprising.
Immigration
The coefficient of the IRCA immigration variable was not significant in the specifications we tried, and usually had a negative coefficient. Hence, we have not included it in the final specification. Our understanding is that "child-only" families are in the Basic program, which is consistent with our earlier interpretation that the finding for the Basic program captures the child-only phenomenon.
Exhibit 5.3
| Regression Results for Unemployed Parent Models | |||||||
| Sample: 19 states, 1979.4 - 1994.3 | |||||||
| Dependent Variable is change in ln(participation/expected participation) a | |||||||
| Coefficients | T-statistics b | ||||||
| Explanatory | Child | Child | |||||
| Variablesc | laga | Caseload | Recipients | Recipients | Caseload | Recipients | Recipients |
| ln(unemployment rate) | a0 | 0.180 | 0.171 | 0.177 | 9.0 | 9.0 | 9.0 |
| (PDL: L = 14)a | 10xa1 | -0.241 | -0.199 | -0.267 | -3.8 | -3.3 | -4.3 |
| 100xa2 | 0.109 | 0.076 | 0.128 | 2.5 | 1.8 | 3.0 | |
| long-run elasticity | 1.283 | 1.244 | 1.148 | ||||
| ln(trade employment per cap.) | a0 | -0.920 | -0.778 | -0.838 | -5.9 | -5.1 | -5.5 |
| (PDL: L = 6)a | 10xa1 | 2.083 | 1.740 | 1.652 | 5.2 | 4.4 | 4.2 |
| long-run elasticity | -2.068 | -1.794 | -2.397 | ||||
| ln(maximum monthly benefit) | current | 0.258 | 0.091 | 0.283 | 1.9 | 0.7 | 2.1 |
| 1st lag | 0.054 | 0.125 | 0.089 | 0.4 | 0.9 | 0.6 | |
| 2nd lag | -0.053 | -0.055 | -0.028 | -0.4 | -0.4 | -0.2 | |
| long-run elasticity | 0.258 | 0.161 | 0.344 | ||||
| average tax and benefit | current | 0.196 | 0.226 | 0.161 | 1.5 | 1.8 | 1.2 |
| reduction rate | 1st lag | -0.109 | -0.160 | -0.074 | -0.8 | -1.2 | -0.5 |
| 2nd lag | -0.083 | -0.145 | -0.051 | -0.7 | -1.3 | -0.4 | |
| long-run effect | 0.004 | -0.080 | 0.036 | ||||
| AFDC earnings cut off | current | -0.015 | 0.011 | -0.027 | -0.3 | 0.2 | -0.5 |
| relative to gross income limit | 1st lag | -0.048 | -0.046 | -0.066 | -0.9 | -0.9 | -1.2 |
| 2nd lag | -0.030 | -0.051 | -0.020 | -0.9 | -1.5 | -0.6 | |
| long-run effect | -0.093 | -0.086 | -0.113 | ||||
| OBRA81 | current | -0.091 | -0.045 | -0.083 | -1.5 | -0.8 | -1.5 |
| 1st lag | -0.009 | 0.024 | 0.014 | -0.1 | 0.4 | 0.2 | |
| long-run effect | -0.100 | -0.020 | -0.069 | ||||
| DEFRA84 | current | -0.004 | 0.008 | 0.007 | -0.1 | 0.3 | 0.3 |
| Seasonal Dummies | Spring | -0.218 | -0.249 | -0.200 | -4.9 | -5.9 | -4.8 |
| Summer | -0.340 | -0.341 | -0.317 | -6.4 | -6.7 | -6.4 | |
| Fall | -0.130 | -0.145 | -0.117 | -2.8 | -3.2 | -2.7 | |
| Calendar Year Dummies | 1979 | 0.576 | 0.687 | 0.566 | 6.2 | 7.6 | 6.4 |
| 1980 | 0.477 | 0.482 | 0.476 | 6.3 | 6.5 | 6.7 | |
| 1981 | 0.416 | 0.291 | 0.382 | 4.3 | 3.1 | 4.2 | |
| 1982 | 0.114 | 0.151 | 0.121 | 1.4 | 1.9 | 1.6 | |
| 1983 | 0.269 | 0.274 | 0.250 | 3.7 | 3.9 | 3.7 | |
| 1984 | 0.200 | 0.204 | 0.210 | 2.6 | 2.7 | 2.8 | |
| 1985 | 0.232 | 0.224 | 0.200 | 3.1 | 3.0 | 2.8 | |
| 1986 | 0.239 | 0.271 | 0.234 | 3.2 | 3.8 | 3.3 | |
| 1987 | 0.239 | 0.217 | 0.210 | 3.3 | 3.1 | 3.1 | |
| 1988 | 0.284 | 0.279 | 0.247 | 3.9 | 3.9 | 3.6 | |
| 1989 | 0.279 | 0.300 | 0.263 | 3.7 | 4.1 | 3.7 | |
| 1990 | 0.259 | 0.296 | 0.241 | 3.5 | 4.1 | 3.5 | |
| 1991 | 0.118 | 0.118 | 0.112 | 1.6 | 1.6 | 1.6 | |
| 1992 | 0.086 | 0.105 | 0.091 | 1.2 | 1.5 | 1.3 | |
| 1993 | 0.170 | 0.196 | 0.170 | 2.2 | 2.7 | 2.4 | |
| 1994 | 0.141 | 0.106 | 0.179 | 1.3 | 1.0 | 1.7 | |
a. Expected participation variable is based on national age-specific participation rates for 1990 and estimated population of the state by age in the quarter.
b. T-statistics in bold are at least 2.0 in absolute value. These statistics were reduced from those calculated by SAS to make a correction for degrees of freedom that is not made by the procedure used (TSCSREG). The reduction factor is .61, computed as [(T-K)/T]5, where T is the number of quarters (60) and K is the number of explanatory variables (38).
c. All explanatory variables except quarter and year dummies are changes. Quarter and year dummies are equal to .25 in the quarters/years indicated so that coefficients can be interpreted as annualized rates of growth.lagged the number of periods indicated. For the polynomial distributed lag (PDL) variables, the coefficient of the variable lagged j periods is ao + a1 j + a2j2 for j=0, 1, 2, ...L. Other variables are lagged the number of periods indicated.
d. Variables are moving average of previous four quarters.
4. Labor Market Variables
As mentioned above, the specification search led us to a specification that is very similar to the final specification for the Basic equations. The final distributed lag specification for the unemployment rate is identical, but the estimated coefficients are much larger. We estimate that a permanent increase in the unemployment rate of one percent (e.g., 5 percent to 5.05 percent) increases the UP caseload by 1.28 percent (.0128 = 1.283 * .01), compared to just 0.16 percent for the Basic caseload. We also estimate that after just six quarters a one percent increase in trade employment per capita reduces the UP caseload by 2.07 percent, compared to 1.00 percent for the Basic caseload. When we omit the trade variable from the specification (a specification not included in the exhibit), the long-run elasticity for the unemployment rate increases from 1.28 to 1.42. Findings for the other participation measures are very similar. We discuss these findings further in Section E, below.
Many have speculated that the effects of the business cycle on AFDC participation are asymmetric, with recessions having a large effect on participation but recoveries having a smaller, or perhaps more delayed, effect in the opposite direction. We tested for asymmetry by estimating a model in which we interacted the three distributed lag variables for the unemployment rate with a dummy variable for the direction of change of the unemployment rate in the current period, yielding separate distributed lags for increases and decreases in unemployment (a "switching" model). The two estimated distributed lags were very similar, and not statistically different. As discussed in the introduction, Steve Thompson has recently been able to find statistical evidence of asymmetry in a monthly time-series model for a Maryland by lagging the switch point. We did not have the resources to experiment with alternative switching specifications. It could be that the estimates we report are a weighted average of stronger business cycle effects in recessions and weaker effects in recoveries.
5. AFDC Program Variables
Program Parameters
The findings for two of the three program parameters included in the specification are very similar to those found for the Basic program, but the findings for the third are a puzzle. We estimate that a one percent increase in maximum monthly benefits increases the caseload by 0.26 percent after two quarters, compared to 0.27 percent for the Basic caseload, and that an increase in the earnings cut-off relative to the gross income limit of 10 percentage points reduces the caseload by 0.9 percent, compared to 1.0 percent for the Basic caseload. The puzzling finding is that the current quarter coefficient for the average tax and benefit reduction rate has the wrong sign and is substantial, although insignificant. Perhaps more importantly, the sum of the coefficients on the current and two lagged values of the variable is essentially zero, compared to -0.15 in the Basic caseload model. Findings for the other participation measures are quite similar to those in the Basic caseload model.
Federal Legislation
The sum of the coefficients on the current and lagged OBRA81 dummy implies a 10 percent reduction in the caseload after one quarter in addition to any reductions due to changes in program parameters, compared to a reduction of seven percent for the Basic caseload. Hence, the point estimates for the two caseloads are very similar, even though the finding for the UP caseload is not statistically significant. The DEFRA84 coefficient is essentially zero, indicating that any effect of DEFRA84 on the caseload is captured by the program parameters and the year dummies. This finding also accords well with the finding for the Basic program.
1115 Waivers
We did not find any statistically significant coefficients for the 1115 waiver dummies in the UP equations.
6. Other Programs and Laws
Of the many variables tried in this category, we found none that were statistically significant. This is consistent with the lack of strong findings for these variables in the Basic equation, and the small number of states in the UP model for the full period.
7. UP Results for 1991 - 1994
FSA-88 mandated that all states have UP programs from October 1990 on. In this section we present estimates of the UP caseload model using data for the post-mandate period. Because the sample period is too short to use the Parks method, we use the alternative, weighted least squares (WLS) method.
The specification we report is somewhat different than the specification reported for the full-period model. We replicated that specification in our first set of post-mandate estimates, but found that the coefficients for the ratio of the ECO to the GIL were very insignificant. The evident reason for this is that the definition of the GIL was not changed during the subperiod. We also added two variables that had been dropped in the full period model because much of the cross-state variation in changes of these variables occurred in the subperiod: the IRCA immigrant variable and the Medicaid expansion variable. In addition, we added interactions between the seasonal dummies and a dummy for six-month UP programs that were introduced in some of the states affected by the mandate, on the expectation that the seasonal pattern for the caseload would differ from the seasonal pattern in states with 12-month programs.
We initially estimated models using changes for the full post-mandate sample, (1991.1 to 1994.3), but obtained results that made little sense. The coefficient for the 1990 year dummy (which estimates the annualized rate of growth from 1990.4 to 1991.1 that is not explained by changes in other variables) was extremely large, and the value for the 1991 coefficient was also very large. We traced the reason for this to the states that began their programs under the mandate. Because they started at zero in 1990.3, they experienced very rapid rates of growth for the first year. This is evident by comparing post-mandate estimates for the 19 states that had programs for the full period (Column 2 of Exhibit 5.4) to results obtained using just the 22 states that started their programs in 1990.4 (Column 4).(13) Dropping the first full year from the sample yields much more credible findings in the mandate states (Column 5), although year dummy coefficients continue to differ substantially from those for the full-period states (compare to Column 3). Hence, when pooling the data for all states, we added an interaction between each year dummy and a dummy for whether or not the state started its program under the mandate.
For the remainder of this section, we focus on the results using data for 49 states for the period 1992.1 through 1994.3 (Column 5) and compare them to estimates for the same model using the full period for the 19 states with UP programs for the full period (Column 1).(14)
The findings for the labor market variables are strong for the post-mandate period, although different in some respects from the full-period estimates. The long-run unemployment elasticity is 0.86 (compared to 0.97) and the long-run trade employment elasticity is -5.7 (compared -2.8). The large trade elasticity is primarily influenced by the data for the mandate states; using that sample alone, the elasticity is -10.3 (Column 5), compared to a post-mandate estimate of -1.7 for the 19 full-period states (Column 3). Hence, there is evidence of very strong business cycle effects, but there are differences in the findings for mandate and non-mandate states. We have not had an opportunity to explore these differences further.
The subperiod findings for the MMB and, especially, the ATBRR are puzzling. For the post-mandate estimates using just the 19 full-period states, the sign of the long-run MMB elasticity is opposite that expected and its magnitude is large. For the 22 mandate states, the sign is positive, as expected, but the coefficient is exceptionally large. When all states are combined, the estimate is credible. The problem may be inadequate independent variation in this variable over the subperiod, especially among the two subsets of states.
We did find significant results for the IRCA immigrant variable, but predominantly in the mandate states. Note that the IRCA coefficient is also significant in the full-period estimates for the 19 full-period states, whereas it was not when we used the Parks method for the full period. This change may be related to other changes in the specification, but it also may be due to the large weight given to California in these estimates.
We did not find evidence of an effect of the Medicaid expansion except marginally in the full-period estimates for the 19 full-period states. Recall, however, that we dropped this variable from the UP specification reported earlier because of its insignificance when we used the Parks method.
Exhibit 5.4
| Regression Results for Post-mandate Unemployed Parent Caseload Models a | ||||||||
| Weighted Least Squares | ||||||||
| Dependent Variable is change in ln(participation/expected participation) | ||||||||
| 19 States with UP Programs | 22 States with | |||||||
| for the Full Sample | Mandated UP Programs | 49 States | ||||||
| Explanatory | 1979.4- | 1991.1- | 1992.1- | 1991.1- | 1992.1- | 1991.1- | 1992.1- | |
| Variables b | 1994.3 | 1994.3 | 1994.3 | 1994.3 | 1994.3 | 1994.3 | 1994.3 | |
| ln(unemployment rate) | a0 | 0.092 | -0.026 | 0.002 | -0.026 | 0.006 | -0.012 | 0.027 |
| (PDL: L = 14) | (6.06) | (-0.85) | (0.05) | (-0.28) | (0.07) | (-0.45) | (1.04) | |
| 100xa1 | -0.422 | 0.793 | 0.634 | 1.652 | 1.082 | 0.756 | 0.371 | |
| (-2.47) | (2.45) | (1.77) | (1.61) | (1.31) | (2.74) | (1.40) | ||
| 1000xa2 | 0.013 | 0.038 | 0.055 | -0.052 | 0.004 | 0.006 | 0.029 | |
| (1.46) | (2.63) | (3.04) | (-0.93) | (0.09) | (0.44) | (2.22) | ||
| long-run elasticity | 0.973 | 0.489 | 0.716 | 1.343 | 1.249 | 0.666 | 0.856 | |
| ln(trade employment per cap.) | a0 | -0.839 | -1.862 | -1.199 | -3.912 | -3.479 | -2.816 | -1.994 |
| (PDL: L = 6) | (-5.85) | (-6.00) | (-3.11) | (-6.29) | (-6.76) | (-12.03) | (-8.61) | |
| a1 | 0.144 | 0.394 | 0.317 | 0.757 | 0.669 | 0.542 | 0.394 | |
| (4.58) | (5.18) | (3.37) | (5.24) | (6.05) | (9.78) | (7.52) | ||
| long-run elasticity | -2.849 | -4.76 | -1.736 | -11.487 | -10.304 | -8.33 | -5.684 | |
| ln(maximum monthly benefit) | current | 0.235 | 0.287 | -0.080 | 0.048 | 1.429 | 0.448 | 0.789 |
| (2.38) | (0.81) | (-0.17) | (0.05) | (1.58) | (1.42) | (2.40) | ||
| 1st lag | 0.141 | -1.305 | -1.112 | -1.933 | 1.170 | -0.769 | 0.111 | |
| (1.31) | (-3.43) | (-2.39) | (-1.67) | (1.30) | (-2.24) | (0.31) | ||
| 2nd lag | 0.040 | -0.183 | -0.493 | 2.616 | 0.019 | 1.351 | 0.106 | |
| (0.41) | (-0.52) | (-1.19) | (2.88) | (0.03) | (4.45) | (0.36) | ||
| long-run elasticity | 0.416 | -1.201 | -1.685 | 0.730 | 2.618 | 1.030 | 1.006 | |
| average tax and benefit | current | 0.216 | -0.083 | 0.044 | 0.194 | -0.206 | -0.177 | -0.223 |
| reduction rate | (2.59) | (-0.64) | (0.29) | (0.39) | (-0.56) | (-1.49) | (-1.98) | |
| 1st lag | -0.211 | -0.107 | -0.034 | 1.190 | 1.180 | 0.141 | 0.134 | |
| (-2.56) | (-0.66) | (-0.18) | (2.11) | (2.78) | (0.99) | (1.06) | ||
| 2nd lag | -0.166 | -0.043 | 0.047 | 1.358 | 1.337 | 0.283 | 0.292 | |
| (-2.82) | (-0.29) | (0.28) | (2.65) | (3.53) | (2.19) | (2.50) | ||
| long-run effect | -0.160 | -0.233 | 0.057 | 2.742 | 2.311 | 0.246 | 0.203 | |
| OBRA81 | current | -0.064 | ||||||
| (-3.23) | ||||||||
| 1st lag | -0.005 | |||||||
| (-0.26) | ||||||||
| long-run effect | -0.069 | |||||||
| DEFRA84 | current | 0.011 | ||||||
| (0.85) | ||||||||
| IRCA immigrants per 100c | 1st lag | 0.326 | 0.365 | 0.040 | 2.109 | 1.647 | 1.035 | 0.458 |
| (2.40) | (1.94) | (0.17) | (2.31) | (1.77) | (4.56) | (1.97) | ||
| Medicaid expansion | current | -0.192 | -0.151 | -0.139 | 1.149 | -0.408 | -0.133 | -0.082 |
| (-1.97) | (-1.21) | (-1.04) | (0.80) | (-0.32) | (-0.98) | (-0.67) | ||
| Seasonal Dummies | Spring | -0.220 | 0.006 | -0.109 | 0.029 | 0.093 | 0.062 | -0.045 |
| (-8.79) | (0.11) | (-1.52) | (0.12) | (0.54) | (1.14) | (-0.82) | ||
| Summer | -0.341 | -0.011 | -0.116 | -0.040 | 0.030 | 0.073 | -0.061 | |
| (-10.71) | (-0.16) | (-1.22) | (-0.18) | (0.19) | (1.16) | (-0.98) | ||
| Fall | -0.140 | 0.147 | 0.002 | -0.143 | -0.159 | 0.210 | 0.069 | |
| (-5.15) | (2.72) | (0.02) | (-0.73) | (-1.11) | (4.17) | (1.31) | ||
| interaction of dummy for states | Spring | -0.240 | -0.192 | -0.170 | -0.240 | |||
| with six-month UP programs and | (-1.55) | (-1.74) | (-1.69) | (-3.12) | ||||
| seasonal dummies | Summer | -0.343 | -0.079 | -0.392 | -0.169 | |||
| (-2.14) | (-0.66) | (-3.71) | (-2.08) | |||||
| Fall | 0.484 | 0.668 | 0.188 | 0.392 | ||||
| (3.07) | (6.00) | (1.88) | (5.09) | |||||
| interaction of dummy for states with | 1991 | 4.954 | ||||||
| UP programs mandated under | (36.66) | |||||||
| FSA-88 and year dummies | 1992 | 0.701 | 0.501 | |||||
| (7.73) | (6.18) | |||||||
| 1993 | 0.368 | 0.300 | ||||||
| (4.06) | (5.30) | |||||||
| 1994 | 0.014 | -0.053 | ||||||
| (0.16) | (-0.93) | |||||||
| 1995 | 0.026 | -0.061 | ||||||
| (0.25) | (-0.95) | |||||||
| Calendar Year Dummies | 1979 | 0.653 | ||||||
| (13.25) | ||||||||
| 1980 | 0.496 | |||||||
| (12.46) | ||||||||
| 1981 | 0.338 | |||||||
| (7.56) | ||||||||
| 1982 | 0.159 | |||||||
| (4.00) | ||||||||
| 1983 | 0.197 | |||||||
| (5.96) | ||||||||
| 1984 | 0.170 | |||||||
| (4.76) | ||||||||
| 1985 | 0.223 | |||||||
| (6.63) | ||||||||
| 1986 | 0.230 | |||||||
| (6.71) | ||||||||
| 1987 | 0.156 | |||||||
| (4.84) | ||||||||
| 1988 | 0.199 | |||||||
| (6.16) | ||||||||
| 1989 | 0.289 | |||||||
| (8.25) | ||||||||
| 1990 | 0.298 | 0.319 | 5.330 | 0.314 | ||||
| (8.24) | (4.27) | (24.36) | (4.59) | |||||
| 1991 | 0.141 | -0.013 | -0.026 | 0.706 | 0.151 | -0.068 | -0.159 | |
| (3.76) | (-0.22) | (-0.36) | (4.14) | (0.95) | (-1.34) | (-2.77) | ||
| 1992 | 0.158 | -0.063 | -0.002 | 0.413 | 0.407 | -0.042 | 0.019 | |
| (4.26) | (-1.24) | (-0.04) | (2.56) | (3.59) | (-0.90) | (0.41) | ||
| 1993 | 0.225 | -0.084 | -0.012 | 0.113 | -0.027 | -0.050 | -0.005 | |
| (6.00) | (-1.41) | (-0.16) | (0.59) | (-0.17) | (-0.92) | (-0.08) | ||
| 1994 | 0.134 | -0.187 | -0.111 | 0.519 | 0.346 | -0.006 | 0.052 | |
| (3.31) | (-2.81) | (-1.29) | (2.26) | (1.88) | (-0.11) | (0.83) | ||
| Auto-Regression Correction | 1st Lag | 0.233 | 0.257 | 0.266 | 0.227 | 0.340 | 0.271 | 0.324 |
| (7.76) | (4.27) | (3.71) | (4.02) | (4.87) | (7.45) | (7.50) | ||
a. T-statistics in bold are at least 2.0 in absolute value.
b. All explanatory variables except quarter and year dummies are changes. Quarter and year dummies are equal to .25 in the quarters/years indicated so that coefficients can be interpreted as annualized rates of growth.lagged the number of periods indicated. For the polynomial distributed lag (PDL) variables, the coefficient of the variable lagged j periods is ao + a1 j + a2j2 for j=0, 1, 2, ...L. Other variables are lagged the number of periods indicated.
c. Variable is amoving average of previous four quarters.
D. AVERAGE MONTHLY BENEFIT EQUATION
1. Determining the Final Specification
The selection of variables for the final average monthly benefit (AMB) equation was largely determined by the findings from the Basic and UP participation models (Exhibit 5.5). We began by including all of the variables that are included in either the final Basic or the final UP participation equations plus dummy variables for the existence and type of UP program (six-month, 12-month, and whether introduced as the result of requirements in FSA88). Except in the case of some program parameters, we then dropped all variables that had coefficients with t-statistics less than one in absolute value.
In interpreting the findings, it is important to keep the following in mind:
- The AMB variable is average monthly benefits for all cases in both the Basic and UP programs;
- The effects of explanatory variables on AMB may be of two types: effects on benefits received by existing AFDC families, and effects that work through changes in the composition of the AFDC caseload;
- The maximum monthly benefit variable in the AMB equation does not include the value of Food Stamps, whereas the same variable in the participation equations does. The reason for this is that the AMB equation itself refers to the AFDC benefits received only; and
- The sample period for this equation does not include the first two and the last four quarters of the period used to estimate the participation equations.
2. Year and Seasonal Effects
As in the participation equations, the coefficients on the year dummies must be adjusted for seasonal effects to obtain estimates of growth not accounted for in each year by variables in the model. The adjustment factor in this case is positive, .036. Only one of the year coefficients is positive, even after the adjustment (.015 for 1985). In many years the negative coefficient is substantial, even after adjustment. The largest negative values are for 1980, 1981, and all years from 1986 to 1991. The largest adjusted value is -.041, for 1980, the next largest is -.028, for 1981 , and the next is -.02, for 1990.
3. Demographic Variables
Population Growth and Aging
We did not include a variable for population growth and aging in the AMB equation.
Exhibit 5.5
| Average Monthly Benefit Regression Results | ||||
| Sample: 51 states, 1980.2 - 1993.3 | ||||
| Dependent Variable is Change in ln(average monthly benefit) | ||||
| Explanatory | ||||
| Variables c | Lag | Coefficient | T-statistic b | |
| ln(unemployment rate) | 100xa0 | 0.656 | 3.7 | |
| (PDL: L = 14) a | 100xa1 | -0.338 | -6.6 | |
| 1000xa2 | 0.223 | 6.7 | ||
| long run elasticity | -0.030 | |||
| ln(trade employment per cap.) | a0 | 0.127 | 14.7 | |
| (PDL: L = 10) a | 10xa1 | -0.615 | -24.9 | |
| 100xa2 | 0.410 | 13.4 | ||
| long run elasticity | -0.406 | |||
| ln(maximum monthly benefit) | current | 0.663 | 73.0 | |
| 1st lag | -0.085 | -9.9 | ||
| 2nd lag | 0.018 | 2.0 | ||
| sum | 0.596 | |||
| average tax and benefit | current | -0.133 | -8.8 | |
| reduction rate | 1st lag | -0.142 | -9.4 | |
| 2nd lag | 0.166 | 11.3 | ||
| sum | -0.109 | |||
| AFDC earnings cut off | current | -0.026 | -3.7 | |
| relative to gross income limit | 1st lag | -0.003 | -0.5 | |
| 2nd lag | 0.059 | 8.8 | ||
| sum | 0.030 | |||
| OBRA81 | current | 0.080 | 9.9 | |
| 1st lag | 0.038 | 4.8 | ||
| 2nd lag | -0.061 | -7.4 | ||
| sum | 0.056 | |||
| DEFRA84 | current | -0.008 | -1.6 | |
| 6-month UP program | current | 0.035 | 4.6 | |
| 12-month UP program | current | 0.013 | 4.5 | |
| UP started in 1990.4 | current | -0.038 | -5.8 | |
| family cap | 1st lag | 0.055 | 3.5 | |
| IRCA immigrants per 100 | 1st lag | * | 0.007 | 1.4 |
| ln(out-of-wedlock births) | d | * | 0.074 | 3.6 |
| ln(% insured unemployed) | 1st lag | 0.032 | 8.0 | |
| abortion: parental consent/notice. | 1st lag | -0.015 | -6.8 | |
| Medicaid restricted | 1st lag | -0.016 | -7.5 | |
| Spring | -0.036 | -4.8 | ||
| Summer | 0.094 | 13.8 | ||
| Fall | 0.086 | 10.5 | ||
| Calendar year | 1980 | -0.077 | -9.1 | |
| 1981 | -0.064 | -5.7 | ||
| 1982 | -0.022 | -2.3 | ||
| 1983 | -0.048 | -6.0 | ||
| 1984 | -0.041 | -4.4 | ||
| 1985 | -0.028 | -3.3 | ||
| 1986 | -0.049 | -6.0 | ||
| 1987 | -0.039 | -4.9 | ||
| 1988 | -0.052 | -6.5 | ||
| 1989 | -0.052 | -6.5 | ||
| 1990 | -0.056 | -6.8 | ||
| 1991 | -0.055 | -6.7 | ||
| 1992 | -0.050 | -6.1 | ||
| 1993 | -0.053 | -4.7 | ||
a For the polynomial distributed lag (PDL) variables, the coefficient of the variable lagged j periods is a0 + a1 j + a2 j2 for j = 0, 1, 2, ... L. Other variables are lagged the number of periods indicated.
b. T-statistics in bold are at least 2.0 in absolute value.
c. All explanatory variables except quarter and year dummies are changes. Quarter and year dummies are equal to .25 in the quarters/years indicated so that coefficients can be interpreted as annualized rates of growth.
d Variables are moving averages of previous four quarters.
Vital Statistics
Only one of the vital statistics variables, out-of-wedlock births, appears in the final AMB specification and it has a significant, positive coefficient. More out-of-wedlock births among existing AFDC families would be expected to increase AMB, but families entering the caseload as the result of a first out-of-wedlock birth would presumably receive lower than average benefits.
Immigration
The IRCA legalizations variable appears in the final specification with a positive, but insignificant, coefficient. The positive coefficient seems at odds with the hypothesis that the large coefficients on this variable in the Basic participation models reflects child-only families; presumably such families would receive lower than average benefits unless the average number of children in such families is substantially larger than average.
4. Labor Market Variables
Unemployment Rate
A one percent increase in the unemployment rate, other things constant, reduces the AMB by an estimated 0.03 percent after 14 months. Equivalently, an increase in the unemployment rate from five to six percent reduces the AMB by 0.6. It seems likely that increases in unemployment, if anything, increase benefits among existing AFDC cases. The negative estimated effect presumably is the result of new cases that receive lower than average benefits -- due to fewer children and/or greater income from other sources.
Trade Employment per Capita
The long-run elasticity of AMB with respect to trade-employment is estimated to be -0.41. Presumably increases in trade employment reduce benefits for families that stay in the caseload, if they have any effect at all. Some families leave the caseload, however, and they may be receiving above or below average benefits. The negative long-run unemployment elasticity, discussed above, suggests that marginal families receive lower than average benefits, but the negative long-run elasticity for trade employment suggests the opposite.
5. AFDC Program Variables
Program Parameters
The variable with the most significant coefficient in the model is, not surprisingly, the current value of the maximum monthly benefit. The current coefficient is a highly significant 0.66, and the coefficients on the first and second lag are both negative, but not significant. The finding suggests that a one percent increase in MMB is immediately translated into an almost equal increase in the average benefits received by existing cases, but that the average benefit might fall as new families enter the caseload and receive lower than average benefits.
The estimated effects of a change in the average tax and benefit reduction rate (ATBRR) are somewhat puzzling and reminiscent of the puzzling findings for UP participation. The pattern of the coefficients would be consistent with the hypothesis that existing AFDC families initially lose benefits, but over time they either recover benefits by reducing other income or marginal families with low benefits leave the caseload -- but this conclusion may be too strong. After two quarters, any initial effects of a change in the ATBRR disappear.
A similar pattern appears in the coefficients of the current and lagged values of the AFDC earnings cut-off (ECO) relative to the gross income limit (GIL). They suggest that a reduction in the GIL, holding ECO constant (i.e., an increase in the ratio) initially reduces AMB, but after two quarters this negative effect is more than offset as, perhaps, some females reduce their other income, thereby increasing benefits, and marginal families with below average benefits leave the roles.
Federal Legislation
The estimated effects of OBRA81 on AMB depend on the coefficients on the OBRA81 variable, the 1981 and 1982 year dummies, and the program parameter coefficients, along with the magnitude of the changes in the parameters that resulted from OBRA81. The estimated impact of DEFRA84 is similarly complex. We discuss their effects in the context of the AMB simulations (Chapter 6).
The effect of the UP programs established in 1990.4 under the mandate of FSA88 depends on both the dummy for mandated programs and the dummies for six-month and twelve-month programs. About half of the 23 states affected introduced six-month programs. The combined coefficients for the 1990.4 dummy and the six-month dummy indicate these states experienced, if anything a small reduction in AMB as a result. The estimates suggest that states which introduced 12-month UP programs in 1990.4 experienced a reduction in AMB as a result, by 2.5 percent (based on the sum of the coefficients for the 1990.4 dummy and the 12-month dummy). This may be because UP families in six-month programs are only in the program in the months when their income from other sources is lowest.
1115 Waivers
The only waiver dummy that appears in the final AMB specification is the dummy for the family cap, and it has a significant coefficient that suggests that this type of restriction increases AMB by 5.5 percent. This is puzzling because we would expect such restrictions to, if anything, reduce benefits for families that would have been AFDC families anyway. It may be that the restrictions discourage small families, with below average benefits, from participating in AFDC, but it seems unlikely that the effect of such a change in the composition of the caseload would be so large. As with the finding in the Basic participation models, there are more likely explanations of this finding: other efforts to reduce caseloads in the three states that imposed family caps; migration of some AFDC families to other states; and chance.
6. Other Programs and Laws
Medicaid
We initially included the Medicaid expansion variable and interaction term in the AMB specification, just as in the final specification for the Basic model, but found that both terms had t-statistics well below one in absolute value. Hence, we dropped them in the final specification
SSI children
We also included the SSI child recipient variable in the initial AMB specification -- again because of the finding in the Basic participation model -- and subsequently dropped it from the specification because the t-statistic was below one in absolute value.
Unemployment Insurance
The log of the percent of unemployed persons who are insured has statistically significant, positive coefficients in the final specification. Given the positive relationship between the UI variable and participation in the Basic program found previously, a likely explanation is that unobserved factors such as administrative tightening of programs have common effects on both UI and AFDC.
Abortion Restrictions
The two abortion dummies have significant, and large, negative coefficients. They suggest that parental consent or notification laws and restrictions on Medicaid payments for abortion each reduce AMB by about 1.5 percent. Interpreting the Basic participation results at face value, these restrictions reduce the caseload by 0.2 and 0.3 percent, respectively, and reduce the number of child recipients by 0.3 and 0.5 percent, respectively. This implies that the number of children per AFDC family is reduced by 0.1 and 0.2 percent, respectively.(15) We would expect this reduction to reduce AMB by a comparable percentage amount. A more plausible explanation of the large effects is one we suggested in the discussion of the participation findings: they may be due to other unobserved efforts in the states that adopted these restrictions to reduce fertility and AFDC participation.
SSA Allowance Rates
We included our measure of SSA's administrative tightening of disability requirements in 1977-78 in our initial AMB specification, but the t-statistic was less than one.
E. FURTHER DISCUSSION OF BUSINESS CYCLE ESTIMATES
In this section we examine the dynamics of the effects of changes in the unemployment rate on the caseload and compare our findings to findings reported by others. All of the findings reported in this section are based on Basic and UP caseload models in which we dropped the trade employment variable (Exhibit 5.6). This was done to simplify the analysis and presentation. The other studies we examine use only the unemployment rate as a business cycle variable, whereas in the models we have reported there are two important business cycle variables. Dropping trade employment increases the magnitude of the unemployment rate coefficients somewhat.
For comparison purposes, we consider the estimated effect of a one percentage point increase in the unemployment rate on the caseload, in percent. In the specification we use, the size of the effect depends on the initial unemployment rate. We assume the increase is from five percent to six percent.
1. The Dynamic Effects of an Unemployment Rate Increase
We consider below the dynamics of the effects of a one-percentage point increase in the unemployment rate (i.e., an increase from 5 percent to 6 percent--a 20 percent increase in the unemployment rate) on the caseload under the two hypothetical scenarios for the unemployment rate series. Under both scenarios, the unemployment rate is constant at 5.0 percent for at least 14 quarters before it increases by one percentage point, to 6.0 percent. Under the "temporary increase" scenario, the rate stays at 6.0 percent for one quarter then returns to 5.0 percent and remains there for at least the next 14 quarters. Under the "permanent increase" scenario, the rate stays at 6.0 percent for at least the next 14 quarters. Assume also that all other factors are constant during the relevant period.
Under both scenarios, the estimated initial effect of the one percentage point increase in the unemployment rate on the caseload is 0.7 percent for the Basic program and 3.7 percent for the UP caseload. Even if the unemployment rate increase is temporary, according to the estimates its effect on the caseload will be felt for the next three and one-half years (Exhibit 5.7). Both caseloads start to decline immediately.(16) The decline is faster for the UP caseload than for the Basic caseload, but the UP caseload increased by much more in the first place. By the end of the second year after the temporary increase, both caseloads are above their original levels by about half the initial increase.
If the unemployment rate increase is permanent, the effects of the increase accumulate (Exhibit 5.8). One year after the change the Basic caseload is 2.8 percent higher than originally and the UP caseload is 14.5 percent higher. The increase continues, but at a decreasing rate. By the end of the second year the Basic caseload is 4.3 percent above its original level and the UP caseload is 20.4 percent higher. The caseloads continue to gradually increase, to 5.7 percent and 25.9 percent higher than their original levels after 3.5 years (14 quarters ).
Real recessions are different than either of these stylized scenarios. The increase in the unemployment rate is usually substantially greater than in this example. For instance, from 1989 to 1992 the unemployment rate increased by about two percentage points, and from 1979 to 1983 it increased by about four percentage points. Hence, the magnitude of a recession's effect may be two to four times as large as indicated here. Second, increases in the unemployment rate of substantial magnitude are seldom if ever as temporary as in the first scenario and do not increase and remain indefinitely constant at a higher level as in the second. Instead, they increase and decrease gradually over long periods. In both recessions in the sample period, they stayed close to their peak levels for about two years. This is well short of the 3.5 years in the permanent change scenario. At the same time, however, in each case the rate stayed above 6.0 percent for at least three years. In fact, for the seven years from 1980 to 1986 the average monthly unemployment rate was at or above 7.0 percent every year.
In summary, according to the estimates a recession can result in very large cumulative increases in both programs' caseloads, and higher caseloads are likely to remain above pre-recession levels for three or more years after the economy recovers.
2. Comparison of Business Cycle Effects to Findings in Previous Studies
The estimates we have obtained for business cycle effects are substantially stronger than those found in the literature. We compare the estimated effect of a one percentage point increase in the unemployment rate, from five to six percent, in our model to estimates obtained by others (Exhibit 5.9). For the Basic program, we also report our results when the vital statistics variables are dropped from the specification because variation in these variables may partly be due to business cycles.
We estimate that the specified increase in the unemployment rate increases the Basic caseload by 5.7 percent after 14 quarters. This increases somewhat when the vital statistic variables are omitted -- to 5.9 percent. The largest finding from other studies for the same unemployment rate change is from Cromwell, et al. (1986), a 1.8 percent increase after just three quarters. The difference is in substantial part due to the use of a longer lag length in our specification: our estimate of the effect after three quarters is much more comparable -- 2.4 percent. We estimate that the specified increase in the unemployment rate increases the UP caseload by about 26 percent after 14 quarters. This estimate is almost identical to the estimate reported by Cromwell et al. after just three quarters. By comparison, we estimate that the increase in the UP caseload is only 12.3 percent after three quarters.
Exhibit 5.6
| Regression Results for Basic and UP Models without Trade Employment Variables | |||||||
| Sample: 51 states, 1979.4 - 1994.3 | |||||||
| Dependent Variable is change in ln(participation/expected participation) a | |||||||
| Coefficients | T-statistics b | ||||||
| Explanatory | Caseload | Caseload | |||||
| Variables c | Basic | UP | Basic | UP | |||
| w/ v.s.d | w/o v.s.d | w/o v.s.d | w/ v.s.d | w/o v.s.d | w/o v.s.d | ||
| ln(unemployment rate) | 10xa0 | 0.037 | 0.038 | 0.205 | 16.7 | 18.0 | 11.2 |
| (PDL: L = 14) | 100xa1 | -0.003 | -0.003 | -0.026 | 4.4 | 4.8 | 4.3 |
| 1000xa2 | 0.000 | 0.000 | 0.001 | 2.0 | 2.1 | 0.3 | |
| long-run elasticity | 0.313 | 0.324 | 1.421 | ||||
| ln(maximum monthly benefit) | current | 0.083 | 0.086 | 0.293 | 5.7 | 6.5 | 2.3 |
| 1st lag | 0.136 | 0.136 | 0.063 | 8.8 | 9.7 | 0.5 | |
| 2nd lag | 0.033 | 0.032 | -0.027 | 2.2 | 2.4 | 0.2 | |
| long-run elasticity | 0.252 | 0.255 | 0.328 | ||||
| average tax and | current | -0.024 | -0.028 | 0.167 | 2.0 | 2.6 | 1.4 |
| benefit reduction rate | 1st lag | -0.066 | -0.068 | -0.150 | 5.1 | 6.0 | 1.2 |
| 2nd lag | -0.029 | -0.030 | -0.108 | 2.4 | 2.8 | 1.0 | |
| long-run effect | -0.119 | -0.127 | -0.090 | ||||
| AFDC earnings cut off | current | -0.049 | -0.050 | -0.029 | 9.3 | 10.3 | 0.5 |
| relative to gross income limit | 1st lag | -0.035 | -0.036 | -0.054 | 6.3 | 7.0 | 1.0 |
| 2nd lag | -0.011 | -0.010 | -0.032 | 2.1 | 2.0 | 0.9 | |
| long-run effect | -0.095 | -0.095 | -0.115 | ||||
| OBRA81 | current | -0.044 | -0.043 | -0.075 | 6.8 | 7.6 | 1.3 |
| 1st lag | -0.030 | -0.029 | 0.013 | 4.2 | 4.7 | 0.2 | |
| 2nd lag | -0.013 | -0.014 | 2.0 | 2.5 | |||
| long-run effect | -0.087 | -0.086 | -0.063 | ||||
| DEFRA84 | current | -0.008 | -0.009 | -0.009 | 2.1 | 2.8 | 0.3 |
| family cap | 1st lag | -0.026 | -0.025 | 3.3 | 3.4 | ||
| IRCA immigrants per 100 | 1st lag | 0.063 | 0.057 | 6.0 | 6.0 | ||
| Medicaid expansiong | current | 0.131 | 0.128 | 2.2 | 2.3 | ||
| Med. exp. x share participatingg | current | -0.888 | -0.855 | 1.7 | 1.8 | ||
| ln(out-of-wedlock births)e | 0.097 | 4.0 | |||||
| ln(marriages)e | -0.129 | 4.7 | |||||
| ln(SSI child beneficiaries) | current | 0.009 | 0.009 | 2.2 | 2.5 | ||
| ln(% insured unemployed) | 1st lag | 0.017 | 0.018 | 5.4 | 5.6 | ||
| abortion: parental consent/notice | 1st lag | -0.003 | -0.003 | 1.7 | 2.1 | ||
| Medicaid restricted | 1st lag | -0.002 | -0.002 | 1.4 | 0.2 | ||
| SSDI initial allowance rate f | -0.064 | -0.057 | 2.9 | 2.6 | |||
| 1979 dummies for: | Alaska | -0.011 | -0.023 | 0.1 | 0.2 | ||
| Hawaii | 0.055 | 0.042 | 0.8 | 0.6 | |||
| D.C. | -0.042 | -0.048 | 1.3 | 1.6 | |||
| Seasonal Dummies | Spring | -0.015 | -0.014 | -0.312 | 2.7 | 3.0 | 7.8 |
| Summer | -0.029 | -0.027 | -0.503 | 5.0 | 5.4 | 11.4 | |
| Fall | 0.009 | 0.010 | -0.239 | 1.7 | 2.3 | 5.8 | |
| Calendar Year Dummies | 1979 | 0.016 | 0.028 | 0.721 | 1.1 | 2.1 | 8.0 |
| 1980 | 0.028 | 0.034 | 0.624 | 2.8 | 3.7 | 8.6 | |
| 1981 | -0.020 | -0.019 | 0.479 | 1.5 | 1.6 | 5.1 | |
| 1982 | -0.016 | -0.014 | 0.201 | 1.4 | 1.4 | 2.6 | |
| 1983 | 0.007 | 0.009 | 0.250 | 0.7 | 1.0 | 3.5 | |
| 1984 | 0.009 | 0.014 | 0.217 | 0.9 | 1.5 | 3.0 | |
| 1985 | 0.037 | 0.046 | 0.292 | 3.7 | 5.3 | 4.1 | |
| 1986 | 0.047 | 0.051 | 0.295 | 4.8 | 5.8 | 4.1 | |
| 1987 | 0.023 | 0.030 | 0.284 | 2.4 | 3.5 | 4.1 | |
| 1988 | 0.039 | 0.045 | 0.330 | 4.1 | 5.2 | 4.7 | |
| 1989 | 0.049 | 0.055 | 0.362 | 4.8 | 6.2 | 5.1 | |
| 1990 | 0.060 | 0.064 | 0.371 | 6.0 | 7.4 | 5.2 | |
| 1991 | 0.051 | 0.058 | 0.232 | 5.1 | 6.7 | 3.3 | |
| 1992 | 0.017 | 0.017 | 0.168 | 1.7 | 2.0 | 2.4 | |
| 1993 | 0.008 | 0.012 | 0.224 | 0.8 | 1.3 | 3.1 | |
| 1994 | -0.009 | -0.009 | 0.185 | 0.6 | 0.7 | 1.7 | |
a. Expected participation variable is based on national age-specific participation for 1990 and estimated population of the state by age in the quarter.
b. T-statistics in bold are at least 2.0 in absolute value. These statistics were reduced from those calculated by SAS to make a correction for degrees of freedom that is not made by the procedure used (TSCSREG). The reduction factor used is .41, computed as [(T - K)/T].5, where T is the number of quarters (60) and K is the number of explanatory variables (50).
c. All explanatory variables except quarter and year dummies are changes. Quarter and year dummies are equal to .25 in the quarters/years indicated so that coefficients can be interpreted as annualized rates of growth. For the polynomial distributed lag (PDL) variables, the coefficient of the variable lagged j periods is a0 + a1 j + a2 j2 for j = 0, 1, 2, ... L. Other variables are lagged the number of periods indicated.
d. Indicates whether vital statistics variables are included (with v.o.) or not (without v.o.). The vital statistics variables are ln(out-of-wedlock births) and ln(marriages).
e. Variables are moving averages of previous four quarters.
f. This variable is the change in the state's SSDI initial allowance rate from 1977 to 1978 times the 1979 year dummy. Special dummies for three states were included due to missing initial allowance data.
g. "Medicaid expansion" is the share of children in the state covered under the Medicaid expansions that began in 1988. "Share participating" is the share of children in the state who were in AFDC families in the year before the expansions began (1987 -- average monthly child recipients divided by population under 19).
Exhibit 5.7
Percent increase in the Caseload from a Temporary One Percentage Point Increase in the Unemployment Rate *
(Based on caseload models excluding trade employment variable.)
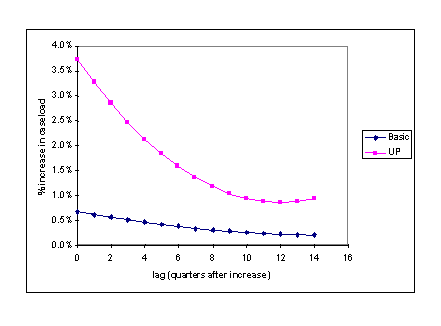
*Assumes unemployment rate increases from five percent to six percent for one quarter, then returns to its previous level. For the jth lag, the percent increase is calculated as bjln(.06/.05), where bj is the coefficient of the jth lag of the log of the unemployment rate.
Exhibit 5.8
Percent increase in the Caseload from a Permanent One Percentage Point Increase in the Unemployment Rate
(Based on models without trade employment)
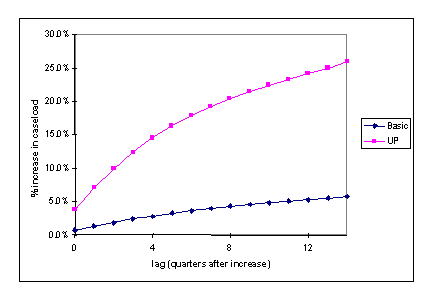
*Assumes unemployment rate increases from five percent to six percent and remains at six percent for the next 14 quarters. For the jth lag, the percent increase is calculated as S ji=0 bjln(.06/.05)
| Exhibit 5.9 | ||||||||
| Estimated Effect of a Permanent One Point Percentage Point Increase in the | ||||||||
| Unemployment Rate on AFDC Caseloads | ||||||||
| Effect on Caseload after Number of Quarters Indicated | ||||||||
| Study | Type | Period | Basic | After | UP | After | Total | After |
| CBO (1993) a | national time-series | quarterly 1973-91 | 1.7% | 4 qtrs. | 9.7% | 6 qtrs. | 2.1% | 6 qtrs. |
| Cromwell et. al. (1986) b | pooled state time-series | quarterly 1976-82 | 1.8% | 3 qtrs. | 25.8% | 3 qtrs. | 3.0% | 3 qtrs. |
| Moffit (1986) d | pooled state time-series | biennial 1967-83 | 0.0% | current year | n.a. | n.a. | n.a. | n.a. |
| Shroder (1995) | pooled state time-series | annual 1982-88 | n.a. | n.a. | n.a. | n.a. | 3.50% | current year |
| Lewin, with vital stats. C | pooled state time-series | quarterly 1979-94 | 2.4% 5.7% | 3 qtrs. 14 qtrs. | 12.3% 25.9% | 3 qtrs. 14 qtrs. | 2.9% 6.7% | 3 qtrs. 14 qtrs. |
| Lewin, without vital stats. C | pooled state time-series | quarterly 1979-94 | 2.4% 5.9% | 3 qtrs. 14 qtrs. | 12.3% 25.9% | 3 qtrs. 14 qtrs. | 2.9% 6.9% | 3 qtrs. 14 qtrs. |
a Estimate for total based on Basic and UP estimates, assuming 5 percent of total caseload is UP.
b Based on data for 44 states, for AFDC Medicaid enrollees. Estimate for Basic is based on results for states without an UP program; estimate for total is based on finding for states with an UP program; and UP estimate is based on the Basic and Total findings assuming that five percent of the caseload is UP.
c Based on specifications without trade employment per capita; inclusion of the later reduces the estimated effect of the unemployment rate, but increases the total effect of business cycles. Basic estimates use data for 50 states and the District of Columbia; UP estimates use data for 19 states with UP programs for the entire sample period. Vital statistics were only included in the Basic equation because of insignificance in the UP equation.
d Based on sample of nine years and an average of 27 states each year.
F. FURTHER DISCUSSION OF PROGRAM PARAMETER EFFECTS
In this section we compare our findings for the program parameters to findings from other studies. As with comparisons of business cycle effects across studies, these comparisons are problematic because of specification differences.
Our estimates of the effects of an increase in the maximum monthly benefit are among the highest found, but one study reports a much larger effect (Exhibit 5.10). We estimate that a one percent increase in this variable increases the Basic caseload by 2.7 percent and the UP caseload by 2.6 percent.(17) Our estimates for the Basic program are larger than those reported by Moffit (1986) or CBO (1993), but Shroder (1995) finds a much larger effect than we do for the combined programs: a 16.7 percent caseload increase. Shroder also uses a pooled state time-series methodology, but with several important differences. One major difference is that he uses instruments for the maximum monthly benefit variable, on the grounds that growth in recipients is likely to cause states to reduce benefit levels. When he does not use the instruments, the estimated effect drops by more than two thirds, to 5.1 percent -- still almost twice as large as our own.
Exhibit 5.10
| Sample | Percent Change in Participation b | ||||
| Study | Type | Period | Basic | UP | Total |
| Ten Percent Increase in Maximum Monthly Benefit | |||||
| CBO (1993) f | national time-series | quarterly 1973-91 | 0.7% | 4.4% | 0.8% |
| Shroder (1995) e | pooled state time-series | annual 1982-88 | n.a. | n.a. | 16.7% |
| Moffit (1986) d | pooled state time-series | biennial 1967-83 | 1.6% | n.a. | n.a. |
| Cromwell et. al. (1986) | pooled state time-series | quarterly 1976-82 | n.a. | n.a. | 1.3% |
| Lewin a | pooled state time-series | quarterly 1979-94 | 2.7% | 2.6% | 2.7% |
| Ten Percentage Point Decrease in Average Tax and Benefit Reduction Rate | |||||
| Moffit (1986) d | pooled state time-series | biennial 1967-83 | 5.5% | n.a. | n.a. |
| Lewin a | pooled state time-series | quarterly 1979-94 | 1.5% | 0.0% | 1.4% |
| Increase in Gross Income limit for 150% to 195% to Need Standard c | |||||
| Lewin a | pooled state time-series | quarterly 1979-94 | 1.3% | 1.2% | 1.3% |
a Basic model includes vital statistics variables; see Exhibit 5.1. Total estimates assume 95 percent of caseloads is in the Basic program.
b Estimate changes may be complete only after several quarters.
c Assumes need standard is identical to AFDC earnings cut off. The change in the gross income limit described is the change that was implemented under DEFRA84.
d Results reported are for random effects estimator. Results for fixed state effects estimator are smaller in magnitude and not statistically significant. Means for the middle year of the sample period (1975) were used in the calculations.
e Based on fixed effects specification with instrumental variables for the maximum monthly benefit variable. Estimate without instruments is about one-third as large.
f Changes calculated at sample means.
We found only one other study that includes an average tax and benefit reduction rate in the specification, Moffitt (1986). Moffit estimates that a 10 percentage point increase in the rate reduces participation in the Basic program by 5.5 percent, compared to our finding of 1.5 percent.
While the reasons that we obtain a smaller effect for the MMB than Shroder and a smaller effect for the ATBRR than Moffitt are unclear, one possible explanation is that we include three benefit variables in our model compared to one for Shroder (MMB) and two for Moffitt (MMB and ATBRR). Neither study, nor any other we have seen, has included a variable for the gross income limit. The sample periods used by both Shroder and Moffitt include years when the GIL changed (twice in Shroder's sample), and it could be that their coefficients for other program parameters are biased away from zero because of this omission. We have not, however, tried to confirm this conjecture.(18)
Notes
1. This constraint could be eliminated through modification of the software or use of an alternative estimation methodology. We estimated some models with SAS-ETS PROC MODEL, a seemingly unrelated regression procedure for estimating linear and non-linear multivariate models. We found, however, that PROC MODEL ran very slowly for our 51 equation model, even though the specification is linear.
2. Like most of the explanatory variables, the vital statistics variables are specified as changes. Initially, however, we included these variables as the current value, based on the argument that they measured flows of families into the pool of families that might participate in AFDC. Multiple lags were included, and we consistently found that the coefficients of the first and second lags were both significant, of opposite signs, and approximately equal in magnitude. Hence, we converted to the change specification.
3. Some have suggested that growth in out-of-wedlock births and declines in marriages have been a more important contributor to caseload growth in the latter part of this period than in the former (see, for instance, CBO, 1993). If so, the coefficients of the vital statistics variables might be larger if estimated using data for the latter part of the period only. To test the idea, we estimated a variant of the final specification in which we included interactions between each of the two vital statistics variables and two dummy variables -- one for the middle third of the sample and one for the last third. The only coefficient that was significant was on the interaction for the marriage variable with the dummy for the last third of the period, and its sign was opposite that expected (coefficient: 0.20; t-statistic: 2.0).
4. We use the level rather than change because legal immigration represents a flow of families into the pool of families that may be eligible for the program.
5. We started with fourth-order polynomials, but found that the third and fourth order coefficients were not significant and could be dropped with little reduction in the fit.
6. In a quadratic DL for a variable, X, the coefficient of the jth lag of the variable, bj, equals a0 + a1 j + 2 j2 for j = 0, 1, ..., L, where the alphas are parameters to be estimated and L is the maximum lag length. If the original model is Yst = ... b0Xst + b1Xst-1 + ... + bLXst-L ..., substitution of the quadratic equation and simplification yields the following alternative version of the model: Yst = ... a0Z0st + a1Z1st-1 + a2Z2st ..., where: Z0st = Xst + Xst-1 + ... + Xst-L; Z1st = Xst-1 + 2 Xst-2 + ... + L Xst-L; Z2st = Xst-1 + 4 Xst-2 + ... + L2 Xst-L. Thus, the alphas can be estimated by replacing the Xs in the model with the Zs. Once the alphas are estimated, the betas can be recovered from the quadratic equation. See Greene (1990).
7. The calculation described in the text yields 3.3 percent, but this somewhat overstates the estimated effect of the assumed change in the unemployment rate because the method used to calculate the effect is only accurate for small percentage changes in the unemployment rate. The exact method--see equation 3.7--yields an estimated increase of 3.0 percent, obtained from .165(ln(.06) - ln(.05)) =.165ln(.06/.05 ) = .030 .
8. From 5.2 percent in 1989.3 to 7.6 percent in 1992.3.
9. The 5.7 percent figure was computed by the exact method, described in the previous footnote, i.e., 0.057 = .313ln(.06/.05).
10. As discussed in more detail in Chapter 2, Yelowitz estimates that increasing the Medicaid need standard by 25 percent of the poverty line reduces the AFDC participation rate of single mothers by 4.6 percent.
11. For a state in which the share of children on AFDC is P, the estimated effect of a change in the share of children eligible for Medicaid under the expanded benefit is .179 - 1.23 x P, which is negative for P >.145.
12. The UP caseload series obtained from ACF reported zero UP cases for the District of Columbia in 1992.2 and 1992.3 and for Mississippi in 1993.4.
13. There are eight states in the sample in addition to the 19 full-period states and the 22 mandate states. These states had UP programs during part, but not all, of the pre-mandate subperiod. Recall that Mississippi and the District of Columbia were dropped from the sample because of evident data errors that could not be corrected. See Chapter 4.
14. The full-period estimates (Column 1) differ from the results reported previously in both specification and estimation methodology. We inadvertently did not include the ratio of the ECO to the GIL in this model. Its exclusion may account for differences in the Park and WLS results for the ATBRR, but we have not had an opportunity to confirm this.
15. The change in the log of children per family (case) equals the change in the log of children minus the change in the log of families. Because small changes in logarithms are approximately equal to percentage changes in the variable itself, the percent change in children per AFDC family is approximately the difference between the percent change in children and the percent change in families.
16. The graph suggests that the effect on both caseloads will continue to be positive for some time after the 14-month period ends; in fact, the effect for the UP caseload appears to be increasing! We specified only a 14-quarter distributed lag because in models in which we included the trade-employment variable the distributed lag coefficients for the unemployment rate became slightly negative in the 15th quarter when we specified long maximum lag lengths. We did not try longer lag lengths without the trade employment variable.
17. The overall figure assumes that five percent of the caseload is in the UP program.
18. One piece of information we have is, at least, consistent with the conjecture. As previously mentioned, we inadvertently omitted the GIL variable from the UP specification when we re-estimated the full-period model using WLS (Exhibit 5.4). Both the MMB and ATBRR coefficients in these findings are much larger than those in the Parks estimates (Exhibit 5.3). Of course, other model and estimation differences could explain these differences. In the WLS results, the long-run MMB elasticity implies that a 10 percent increase results in an UP caseload increase of 4.2 percent -- close to Shroder's 5.1 percent finding when he does not correct for simultaneity, but well short of the 16.7 percent figure he obtains when he makes the correction. The estimated long-run ATBRR effect implies that a 10 percentage point increase in that variable reduces the caseload by 1.6 percent -- in line with our finding for the Basic program (1.5 percent), but well below Moffit's estimate (5.5 percent) for the Basic program.
CHAPTER SIX: SIMULATIONS
A. INTRODUCTION
In this chapter we present sample period caseload and average monthly benefit (AMB) simulations produced by the model, and compare simulated to actual growth. The purpose of the exercise is to provide insights into the size and relative importance of various causes of change in the past. In Section B we present simulations for national caseload and AMB series, and in Section C we present simulations for four selected states: California, Florida, Maryland, and Wisconsin. Concluding comments appear in Section D.
We decompose average annual caseload and AMB growth during selected sample subperiods and the full sample period into growth accounted for by the model and growth not accounted for. Accounted for growth is further decomposed into growth accounted for by five sets of factors: population growth and aging; vital statistics; labor market variables; AFDC program variables; and the miscellaneous other variables included in each model.(1) With one exception, we present separate simulations for the Basic and UP programs; the exception is for Florida, which did not have an UP program for the full sample period.
We do not include the year dummies in the simulated series. If we included them, the simulated series would track the actual series quite closely. We exclude them from the simulations to demonstrate the extent to which variation in the actual series reflects variation in the state-level variables we have included in the model. The year dummies capture national factors, such as changes in federal programs that apply equally to all states (e.g., many aspects of AFDC-related legislation), and the average effects of state-level variables that have not been captured in the model.
The models used in the simulations are the caseload models reported in Exhibits 5.1 and 5.3. The national UP caseload simulations are for the 19 states with UP programs for the full sample period. We also present graphs showing the relationship between actual and predicted caseload growth during the sample period. These show the timing and magnitude of significant departures between the actual and predicted series, and may provide clues about the causes of such departures.
We divide the sample period into four subperiods, corresponding roughly to periods of national economic recession and expansion: the first four years from 1979.4 to 1983.3 include the "double-dip" recession of 1980 and 1981-82; the next period, the six years from 1983.4 through 1989.3, is one of sustained economic growth; the third period, the four years from 1989.4 to 1993.3, encompasses the recession of 1990-91; and the final year, from 1993.4 to 1994.4, is one of substantial expansion.(2) The first subperiod also includes the implementation of OBRA81, while the second includes the implementation of DEFRA84, and the third includes the implementation of FSA88.
B. NATIONAL SIMULATIONS
1. Basic Caseload
1979.4 - 1983.3 Subperiod
For this four-year subperiod, average annual growth of the Basic caseload was essentially zero, but zero growth was the net effect of very large, offsetting changes (Exhibit 6.1, top section). According to our estimates, the labor market variables account for average annual caseload growth of 2.1 percentage points per year and AFDC benefit reductions account for a decline of 4.6 percentage points per year. This probably understates the impact of benefit reductions associated with OBRA81 because the estimated effects of the benefit reductions do not include any effects of OBRA81 that are captured by the calendar year dummies for 1981 and 1982; after adjusting for seasonal factors, the coefficients of these dummies imply reductions of 2.8 and 1.0 percentage points that might also be attributable to OBRA81. In total, the findings imply that OBRA81 reduced the Basic caseload by approximately 20 percent, after controlling for other factors.
Another important, but less widely recognized, feature of this period is that the population in the age group most at-risk for participating in AFDC was growing at a rapid rate as the tail-end of the baby boom generation -- those born in the early 1960s -- was entering the age group; those born in the year usually recognized as the last baby boom year, 1964, turned 16 in 1980. According to our estimates, this growth contributed 2.0 percentage points per year to average annual caseload growth during the period. Changes in the vital statistics variables and in other variables in the model made modest contributions to growth.
1983.4 - 1989.3 Subperiod
During this subperiod the caseload grew at an average annual rate of 1.0 percent. According to our estimates, economic growth reduced the annual growth rate of the caseload by approximately 3.3 percentage points. The AFDC benefit changes captured by the state-level variables made a positive contribution of 0.2 percentage points per year. The effect of AFDC program changes are likely understated in the simulations, however, because the state-level variables do not fully reflect changes mandated by DEFRA84 and other federal legislation that
partially reversed some of the changes of OBRA81. Growth accounted for by population growth and aging declined from 2.0 percentage points in the previous period to 0.5 percentage points as the smaller post-baby boom cohort began entering the at-risk age group. The vital statistics variables contributed 0.7 percentage points per year. The state level factors in the model accounted for nearly all the growth during this period.
Overall, the model predicts an average annual decline of 1.8 percent per year. Given actual average growth of 1.0 percent, growth of 2.8 percentage points was due to other factors not captured in the model.
| Exhibit 6.1 | ||||||||
| Decomposition of National Caseload and Average Monthly Benefit Series | ||||||||
| Average Annual Growth Rate | Annual Growth Rate Accounted for by: | |||||||
| Program, Period, and Model | Actual | Accounted for by Model | Not Accounted for by Model | Population Growth and Aging | Vital Statistics Variables | Labor Market Variables | AFDC Benefits | Other Variables |
| Basic | ||||||||
| 1979.4 - 1983.3 | 0.0% | -0.1% | 0.1% | 2.0% | 0.3% | 2.1% | -4.6% | 0.2% |
| 1983.4 - 1989.3 | 1.0% | -1.8% | 2.8% | 0.5% | 0.7% | -3.3% | 0.2% | 0.1% |
| 1989.4 - 1993.3 | 6.5% | 3.8% | 2.7% | 0.1% | 0.5% | 1.5% | 0.1% | 1.7% |
| 1993.4 - 1994.3 | 0.4% | 0.8% | -0.3% | -0.4% | 0.5% | -0.8% | 1.3% | 0.2% |
| 1979.4 - 1994.3 | 2.2% | 0.4% | 1.8% | 0.8% | 0.5% | -0.4% | -1.0% | 0.5% |
| Unemployed Parent 1 | ||||||||
| 1979.4 - 1983.3 | 25.1% | 12.2% | 12.9% | 1.7% | n.a. | 15.3% | -4.9% | n.a. |
| 1983.4 - 1989.3 | -7.9% | -15.4% | 7.5% | 1.2% | n.a. | -16.6% | 0.6% | n.a. |
| 1989.4 - 1993.3 | 13.1% | 13.0% | 0.1% | 0.7% | n.a. | 12.8% | -0.4% | n.a. |
| 1993.4 - 1994.3 | 0.0% | -1.7% | 1.7% | -0.3% | n.a. | -0.3% | -1.1% | n.a. |
| 1979.4 - 1994.3 | 7.0% | 0.9% | 6.1% | 1.4% | n.a. | 0.9% | -1.4% | n.a. |
| Average Monthly Benefit | ||||||||
| 1980.4 - 1983.3 | -3.3% | 0.8% | -4.1% | n.a. | 0.2% | -0.2% | 1.1% | -0.3% |
| 1983.4 - 1989.3 | -0.2% | 0.5% | -0.7% | n.a. | 0.5% | 0.1% | -0.1% | 0.0% |
| 1989.4 - 1993.3 | -4.1% | -1.7% | -2.3% | n.a. | 0.3% | -0.3% | -1.9% | 0.2% |
| 1980.4 - 1993.3 | -2.0% | 0.0% | -1.9% | n.a. | 0.4% | -0.1% | -0.3% | 0.0% |
| 1. The UP caseload model does not include the vital statistic variables and the AMB model does not include a variable for population growth and aging. The UP caseload simulations are for the 19 states with UP programs throughout the sample period only. | ||||||||
1989.4 - 1993.3 Subperiod
This four-year period is one of very rapid growth in the Basic caseload, at an average rate of 6.5 percent per year. According to the model, the deteriorating economy accounts for 1.5 percentage points of that growth, and the vital statistics variables account for another 0.5 percentage points. The variables in the "other" category contributed a substantial amount (1.7 points per years); this is primarily attributable to the IRCA immigration variable. AFDC benefit changes captured in the state-level variables contributed just 0.1 percentage points to growth. Again, this neglects any effects of federal legislation that might be picked up by the year dummies. The contribution of population growth and aging continues to decline, to 0.1 percentage points per year. The estimated effects of all state-level factors in the model account for 3.8 percentage points of annual growth, combined, leaving 2.7 percentage points attributable to other factors that could not be measured in the model .
1993.4 - 1994.3 Subperiod
Caseload growth decelerated sharply in the last year of the sample period, to just 0.4 percent. The model also predicts decelerated growth, although not as low as actual growth--0.8% compared to 0.4%. Two factors account for the slow growth: an improving economy contributes -0.8 percentage points and a decline in the size of the at-risk population contributes -0.4 percentage points. These factors are offset by growth attributable to the vital statistics variables of 0.5 percentage points and by the AFDC benefit variables of 1.3 percentage points. The latter growth is attributed to the effect that the expansion of the EITC had on the average tax and benefit reduction rate. Additional factors that could not be measured by the model caused slight declines in the caseload, accounting for the difference between 0.4% and 0.8%
Full Period Findings
The average annual growth rate of the Basic caseload over the period was 2.2 percent. Of this growth, 0.4% per year is attributable to state level factors in the model. Thus, 1.8 percentage points per year of growth are due to factors outside of the model. This disguises the fact, however, the state-level factors and the two federal legislation dummies (OBRA81 and DEFRA84) in the model substantially help explain the large cycles in growth during the period. It also hides the fact that some factors in the models made substantial positive contributions to growth over the period and others made offsetting negative contributions.
Positive contributions come from three identified sources. First, population growth and aging contributed an average of 0.8 percentage points per year. Second, declines in marriage and increases in out-of-wedlock births (the vital statistics variables) contributed average growth of 0.5 percentage points per year. Third, other variables -- especially the IRCA immigration variable -- account for average growth of 0.5 percentage points per year.
Offsetting the factors contributing to positive growth were improvements in the labor market and reductions in benefits. According to the model, these latter factors reduced growth by an average of 0.4 and 1.0 percentage points per year, respectively.
Most of the difference in growth between the predicted and actual series occurs between 1983.4 and 1991.4. This is evident in Exhibit 6.2 (top panel) where we plot the two series. As in Exhibit 1.1, we have graphed logarithms of the caseload, so the slope of each series plot represents the growth rate. The predicted series is normalized to equal the actual series in 1989.4. That is, we use 1989.4 as the base period for the predictions and predict forward and backward from that quarter We have also plotted series showing the contributions of the labor market variables and the IRCA variable.(3) It seems likely that the cause of the substantial divergence in the actual and predicted series is the result of several factors not captured in the state-level variables. We discuss this issue further in Section D, after examining the other simulations.
2. Unemployed Parent Caseload
1979.4 - 1983.3 Subperiod
Much of the UP caseload growth came in the first four years of the sample period, in which the average annual growth rate was just over 25 percent (middle section of Exhibit 6.1). The model accounts for just under half of that growth. As with the Basic caseload, growth accounted for by the model during this period is the result of offsetting factors. We estimate that the recession contributed 15.3 percentage points to annual growth, that population growth and aging contributed 1.7 percentage points, and that cuts in benefits reduced average growth by 4.9 percentage points. The last of these figures is almost identical to the corresponding figure for the Basic caseload: -4.6 points.
The exceptionally high growth of the UP caseload relative to predicted growth during this subperiod is a puzzle. We are not aware of any major factors that would account for such rapid expansion other than the double-dip recession. It may be that the estimated effects of labor market factors, although large, substantially understate the recession's impact.
1983.4 - 1989.3 Subperiod
During this period the UP caseload declined at an average annual rate of 7.9 percentage points, but the model predicts an even larger decline, of 15.4 percent. The model's prediction stems from the estimated impact of growth in the economy, -16.6 percentage points, offset by a 1.2 percentage point increase attributed to population growth and aging, and an 0.6 percentage point increase attributed to AFDC benefit expansions.
Exhibit 6.2
Actual and Predicted Caseloads, 1979.4 - 1994.3*
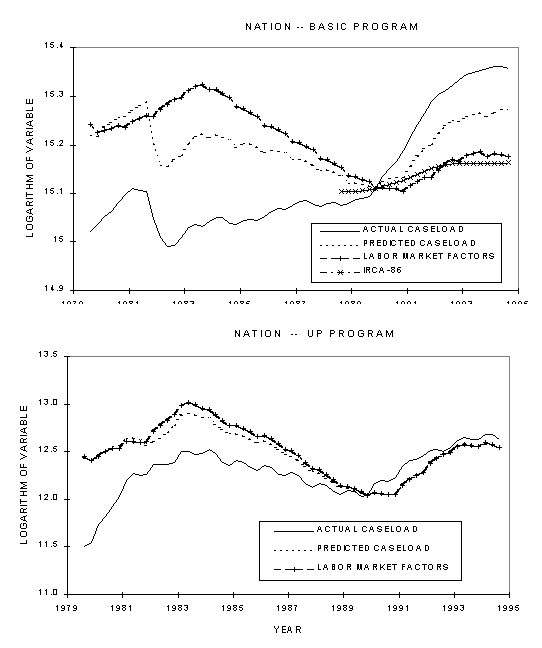
* The predicted caseload series in each graph is normalized to equal the actual series in 1989.4. That is, we use 1989.4 as the base quarter and predict forward and backward from that point. The highest of the "labor market" series above the 1989.4 caseload shows the contribution of labor market factors relative to their contribution in 1989.4. A similar interprediction applies to the IRCA-86 series
1989.4 - 1993.3 Subperiod
During this period the UP caseload again increased very rapidly, an average of 13.1 percent per year. The model predicts growth of 13.0 percent per year -- a surprisingly accurate prediction given the model's performance in the previous nine years. Predicted growth is primarily due to labor market factors (12.8 percentage points), augmented by 0.7 percentage points from population growth and aging and offset by -0.4 percentage points from AFDC benefit changes. Curiously, the estimated effects of AFDC benefit changes on the UP and Basic caseloads during this period and the last year of the full period are opposite in sign. We discuss this further below
1993.4 - 1994.3 Subperiod
There is essentially no growth in the actual UP caseload during the last year of the sample, although the model predicts negative growth of 1.7 percent. The prediction is a combination of negative contributions from three factors; population growth and aging of (-0.3 percentage points), economic recovery (-0.3 percentage points), and changes in the AFDC benefit variables (- 1.1 percentage points).
The large reduction attributed to the AFDC benefit variables is in sharp contrast to the positive 1.3 percentage points that we estimate these same factors contributed to Basic caseload growth during the same year. The reason for this difference is differences in the coefficients of the average tax and benefit reduction rate in the two models. We estimate essentially no long-run effect for the UP caseload, and a negative effect for the Basic caseload. The long-run finding for UP is, however, the result of substantial offsetting coefficients on the ATBRR variable in the first two quarters of the change. The timing of the EITC change is such that the model's predictions for this subperiod reflect the current quarter effect, but not the second quarter effect.
Full Period Findings
In the 19 states with UP programs, the UP caseload grew at an average annual rate of 7.0 percent over the full period, while the predicted caseload grew at an average rate of 0.9 percent. The divergence between the actual and predicted series differs in timing from that for the corresponding Basic series (Exhibit 6.2). Most of the divergence for the Basic series occurs between 1984 and 1991. The greatest divergence for the UP series occurs in the first two years of the sample, through 1981. The actual series continues to grow at a rate that is above that for the predicted series through 1989, but from 1990 on the series move roughly in parallel.
3. Average Monthly Benefits
Due to data constraints the AMB simulations (bottom section of Exhibit 6.1) are for a slightly different period than the caseload simulations -- 1980.4 to 1993.3 instead of 1979.4 to 1994.3. The first of the three subperiods examined differs from the corresponding subperiod for the caseload simulations -- the first year of the four-year period used in the latter is omitted in the former -- and the last one-year subperiod is omitted for lack of data.
1980.4 - 1983.3 Subperiod
This period includes the implementation of OBRA81. The model predicts that implementation of the various provisions of OBRA81 increased AMB substantially; the average annual percentage point increase in this period due to the AFDC benefit variables is 1.1 percent. Yet actual AMB declined, at an average annual rate of 3.3 percent. The labor market and other variables in the model predict small declines, but the model obviously misses the major source of the decline. According to the estimates, changes in the AFDC benefit variables increased, rather than decreased, AMB over the period. These variables, however, do not include the effects of OBRA81 that are captured by the year dummies. The dummy coefficient for 1981 is -.048 (4.8 percent) after adjusting for seasonality. The adjusted coefficient for the previous year, however, is even larger in magnitude (-.063) suggesting that the changes not captured by the model that account for the AMB decline during this period occurred in advance of OBRA81. These could be changes external to the program that affect the composition of the caseload or the benefits they receive, or program changes that are not picked up by the model (e.g., tightening of rules concerning disregards.)
1983.4 - 1989.3 Subperiod
Actual AMB fell slightly during this period, while the model predicts growth of 0.5 percent per year. The source of the predicted growth is primarily the vital statistics variables.
1989.4 - 1993.3 Subperiod
AMB also fell at a rapid rate during this period -- -4.1 percent per year. While the model predicts some decline, the size of the predicted decline (1.7 percent per year) is substantially smaller. The factor driving the model's predictions is changes in the AFDC benefit variables.
Full Period
Average monthly benefits declined substantially over the full period, at an average annual rate of 2.0 percent. This decline is not predicted by the state-level variables in the model, however; instead, they predict no change.
One intriguing finding is that the average annual percent decline in AMB that is not accounted for by the state-level variables is approximately equal to the average annual percent increase in the caseload that is not accounted for by the same variables.(4) The implication of this finding is that the model accounts for essentially all of the long-term growth in total expenditures (i.e., in the product of the caseload and AMB). An analogous finding applies to the subperiod from 1989.4 to 1993.3, but not in other subperiods. While the finding is intriguing, we know of no reason to think that it is other than fortuitous.
C. SIMULATIONS FOR SELECTED STATES
1. California
Basic Caseload
The Basic caseload in California grew at an average annual rate of 3.9 percent over the entire period, almost twice as fast as the national rate. The model predicts average annual growth of 3.3 percent (top section of Exhibit 6.3). According to the model, the main contributors to growth were population growth and aging (1.7 percentage points per year), and the "other" variables -- primarily legalizations under IRCA (1.7 percentage points per year). Changes in the vital statistics and labor market variables made smaller positive contributions, while reductions in AFDC benefits had a substantial offsetting effect (-1.1 percentage points per year).
In most ways, the simulations indicate that California's experience over this period mirrors the experience of the rest of the country, but with differences in the magnitudes of the various effects. The most significant differences are:
- Population growth and aging played a significantly greater role in California -- over twice as large as for the country as a whole. This factor alone accounts for 0.9 percentage points of the 1.7 percentage point difference between California's average caseload growth rate and that for the entire country. Another interesting feature is that the decline in this factor's influence over time is much greater in California; in fact, in the last year of the sample period this factor contributed -0.8 percentage points to caseload growth, compared to -0.4 percentage points in the country as a whole, presumably reflecting a reversal of cross-state migration patterns.
- The estimated contribution of the labor market variables to growth in California's Basic caseload during the 1989.4 to 1993.3 period is over twice as large as their contribution to growth in the national caseload (3.4 percentage points per year vs. 1.5 nationally). This reflects the fact that California's recession was deeper and longer than that for the country as a whole.
- The estimated contribution of the "other" variables -- primarily the IRCA immigration variable -- to growth in California's Basic caseload is much greater than for the country as whole. The difference in growth attributed to this factor over the whole period (1.2 percentage points per year), together with the difference for the population and aging factor, more than accounts for the difference between caseload growth in California and in the country as a whole. In the four years from 1989.4 to 1993.3, when most legalizations occurred, the average annual contribution of the other factors to growth in California's Basic caseload was 5.5 percentage points. According to Werner Schink, this finding is consistent with the large numbers of "child-only" cases opened in California during this period, although we have not had an opportunity to compare the magnitude of such openings to the predictions of the model.
| Exhibit 6.3 | ||||||||
| Decomposition of California Caseload and Average Monthly Benefit Series | ||||||||
| Average Annual Growth Rate | Annual Growth Rate Accounted for by: | |||||||
| Program, Period, and Model | Actual | Accounted for by Model | Not Accounted for by Model | Population Growth and Aging | Vital Statistics Variables | Labor Market Variables | AFDC Benefits | Other Variables |
| Basic | ||||||||
| 1979.4 - 1983.3 | 2.1% | 0.8% | 1.2% | 3.2% | 0.2% | 1.8% | -4.5% | 0.2% |
| 1983.4 - 1989.3 | 2.8% | 0.6% | 2.2% | 1.9% | 0.8% | -2.7% | 0.2% | 0.4% |
| 1989.4 - 1993.3 | 7.5% | 9.7% | -2.2% | 0.4% | 0.7% | 3.4% | -0.3% | 5.5% |
| 1993.4 - 1994.3 | 3.2% | 4.1% | -0.9% | -0.8% | 1.1% | 2.2% | 1.1% | 0.4% |
| 1979.4 - 1994.3 | 3.9% | 3.3% | 0.6% | 1.7% | 0.6% | 0.5% | -1.1% | 1.7% |
| Unemployed Parent 1 | ||||||||
| 1979.4 - 1983.3 | 23.1% | 10.1% | 13.0% | 3.6% | n.a. | 11.1% | -4.6% | n.a. |
| 1983.4 - 1989.3 | -3.1% | -10.7% | 7.6% | 2.7% | n.a. | -13.6% | 0.2% | n.a. |
| 1989.4 - 1993.3 | 19.2% | 18.8% | 0.4% | 1.0% | n.a. | 18.7% | -0.8% | n.a. |
| 1993.4 - 1994.3 | 9.1% | 5.2% | 3.9% | -0.5% | n.a. | 7.2% | -1.6% | n.a. |
| 1979.4 - 1994.3 | 10.6% | 3.8% | 6.9% | 2.3% | n.a. | 3.0% | -1.5% | n.a. |
| Average Monthly Benefit | ||||||||
| 1980.4 - 1983.3 | -2.2% | 2.6% | -4.8% | n.a. | 0.4% | -0.2% | 2.4% | 0.0% |
| 1983.4 - 1989.3 | 1.0% | 1.2% | -0.2% | n.a. | 0.6% | 0.1% | 0.4% | 0.0% |
| 1989.4 - 1993.3 | -6.6% | -3.0% | -3.6% | n.a. | 0.5% | -0.4% | -3.7% | -0.7% |
| 1980.4 - 1993.3 | -2.1% | 0.2% | -2.3% | n.a. | 0.5% | -0.1% | -0.4% | 0.2% |
| 1. The UP caseload model does not include the vital statistic variables and the AMB model does not include a variable for population growth and aging. | ||||||||
The contributions and timing of labor market factors and IRCA immigration to growth in California's Basic caseload are illustrated in Exhibit 6.4 (top panel), where we also compare predicted and actual caseload growth for the whole period. The model's state-level factors and federal legislation dummies predict caseload growth that is slower than actual growth over the period from the beginning of the sample through 1989, with the greatest divergence in growth rates occurring from 1984 on -- just as for the national caseload. From 1989 to 1992 the series move closely together. After 1992 predicted growth exceeds actual growth.
UP Caseload
Over the entire sample period, California's UP caseload also grew at a rate substantially faster than that for the nation -- 10.6 percent per year vs. 7.0 percent nationally (Exhibit 6.3, middle section).(5) As with the national caseload, the periods of greatest growth in the California UP caseload were 1979.4 - 1983.3 and 1989.4 - 1993.3; growth during the latter subperiod was especially strong in California (19.2 percent per year). Just as with the national caseload, the model predicts less than half of the growth of the California caseload in the earlier subperiod, predicts a larger decline than actually occurred in the following subperiod, but predicts most of the growth in the 1989.4 - 1993.3 subperiod. The labor market variables dominate the predicted series.
Werner Schink offered the following additional information about the history of the California caseload and suggestions for further analysis:
- About 90 percent of refugees in California have been continuously on welfare since entering the country. Refugees are not captured in the model and, although relatively small in number, could help explain substantial caseload growth in California;
- Two thirds of AFDC recipients in California score in the lowest decile on the Armed Forces Qualifying Test and 90 percent are in the lowest quarter. Measures of labor market strength that are more focused on low-skill jobs might improve the model's performance;
- About two thirds of UP cases in California eventually transition to Basic. The model's specification does not reflect this; and
- In California, it would be helpful to build separate models by racial/ethnic groups because their experiences are very different.
Exhibit 6.4
Actual and Predicted Caseloads for California, 1979.4 - 1994.3
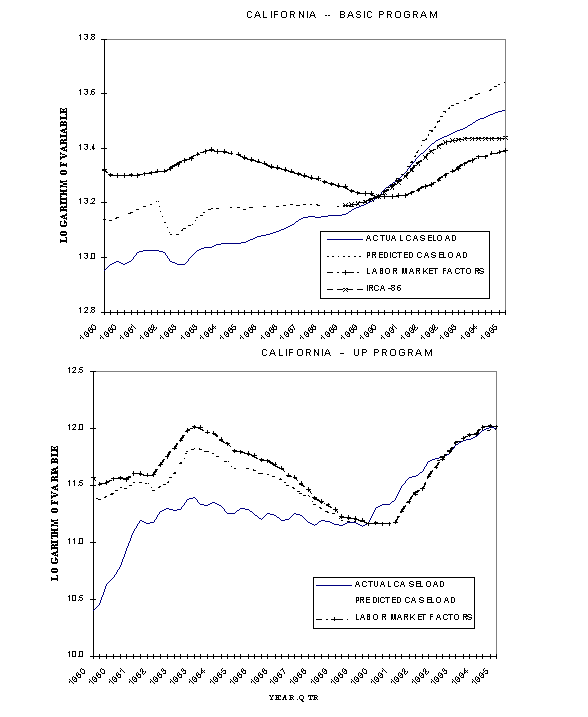
Michael Wiseman also reviewed our findings for California and compared them to his own findings in a recent time-series analysis of openings and closings. According to Wiseman, his model tracks the California caseload better than our model, as we would expect (see Chapter 2). The primary reason apparently is better measures of demographic variables than are available in other states.(6)
Average Monthly Benefits
The results of the AMB simulation for California (Exhibit 6.3, bottom section) are very similar to those for the country as a whole: actual AMB declines at an average annual rate of 2.1 percent, but the model predicts a small increase; the average rate of decline was 2.2 percent in the first three-year subperiod, but the benefit variables predict a 2.4 percentage points annual increase (again, not reflecting the effects of OBRA81 captured by the year dummies); and recent changes in benefits account for at least part of the decline in AMB during the last four-year subperiod. The AMB decline in the last subperiod was substantially larger in California than in the country as a whole (6.6 percentage points per year vs. 4.1 percentage points) and changes in the benefit variables account for more (3.7 percentage points per year vs. 1.9 percentage points).
2. Florida
Basic Caseload
The Basic caseload in Florida grew at an average annual rate of 6.9 percent over the entire period, more than three times as fast as the national Basic caseload. The model predicts average annual growth of just 2.8 percent (top panel of Exhibit 6.5). The main contributors to growth that are accounted for by the model were population growth and aging (2.8 percentage points per year). Changes in the vital statistics and "other" variables -- primarily IRCA legalizations -- contribute about half a percentage point each to annual growth, while the labor market variables and AFDC benefit variables are estimated to have reduced growth by about a half a percentage point each.
The most notable feature of the Florida simulations is the extraordinarily high average annual growth rate of the actual caseload from 1989.4 to 1993.3, 17.5 percent. The model predicts only 5.7 percent annual growth during that period. As in California and the nation as a whole, the labor market variables and the IRCA immigration variable are the main factors accounting for growth during this period. This finding suggests that we have missed a very important factor for Florida during this period which, if we could identify and model it, might substantially improve the model's ability to predict caseload growth in both Florida and other states.
| Exhibit 6.5 | ||||||||
| Decomposition of Florida Caseload and Average Monthly Benefit Series | ||||||||
| Average Annual Growth Rate | Annual Growth Rate Accounted for by: | |||||||
| Program, Period, and Model | Actual | Accounted for by Model | Not Accounted for by Model | Population Growth and Aging | Vital Statistics Variables | Labor Market Variables | AFDC Benefits | Other Variables |
| Basic | ||||||||
| 1979.4 - 1983.3 | 5.4% | 4.2% | 1.2% | 6.0% | 0.5% | 1.7% | -4.2% | 0.1% |
| 1983.4 - 1989.3 | 2.7% | 0.3% | 2.4% | 2.4% | 0.4% | -3.2% | 0.5% | 0.2% |
| 1989.4 - 1993.3 | 17.5% | 5.7% | 11.8% | 0.9% | 0.4% | 2.3% | 0.3% | 1.8% |
| 1993.4 - 1994.3 | -4.6% | 0.1% | -4.7% | 0.4% | 0.0% | -1.6% | 1.1% | 0.2% |
| 1979.4 - 1994.3 | 6.9% | 2.8% | 4.1% | 2.8% | 0.4% | -0.4% | -0.7% | 0.6% |
| Unemployed Parent 1 | ||||||||
| 1979.4 - 1983.3 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| 1983.4 - 1989.3 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| 1989.4 - 1993.3 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| 1993.4 - 1994.3 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| 1979.4 - 1994.3 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| Average Monthly Benefit | ||||||||
| 1980.4 - 1983.3 | -2.3% | 3.5% | -5.8% | n.a. | 0.6% | 0.2% | 3.2% | -0.6% |
| 1983.4 - 1989.3 | 0.5% | -0.8% | -0.3% | n.a. | 0.5% | 0.2% | 0.1% | 0.0% |
| 1989.4 - 1993.3 | -0.9% | -1.1% | 0.3% | n.a. | 0.3% | -0.5% | -1.3% | 0.3% |
| 1980.4 - 1993.3 | -0.6% | 0.8% | -1.4% | n.a. | 0.5% | 0.0% | 0.4% | -0.1% |
| 1. Florida did not have an UP program for the entire sample period and therefore was not included in the sample for the UP model. The AMB model does not include a variable for population growth and aging. | ||||||||
Donald Winstead commented on several aspects of the Florida experience that are not captured in the model:
- Most of the growth from 1989 on was in one county, Dade. Growth in the rest of the state was roughly in-line with the model's predictions.
- Insufficient program capacity, which is not captured in the model, may contribute to the impact of a recession. He writes, "the 1989 recession so overpowered our ability to process work that the resulting impact became virtually exponential. Perhaps an analogy would be the impact of a traffic accident on the beltway at 3:00 a.m. vs. 5:00 p.m."(7) Difficulties with a new computer system exacerbated the administrative problems that were created by the flood of applications.
- The AFDC caseload may be a leading indicator of a recession, increasing before the unemployment rate does because "people at the economic margin are often the first affected by a downturn."
Florida's Medicaid expansion and outreach efforts, starting in 1988 may have had a substantial impact. These included outposting of over 400 eligibility workers in major public hospitals. This effort in combination with Florida's integrated eligibility process for AFDC, Food Stamps, and Medicaid resulted in the identification of many AFDC eligible families.
Two other features of the Florida simulation are especially noteworthy:
- The contribution of population growth and aging is estimated to be 6.0 percentage points per year during the first four years of the sample period. As in the nation as a whole, it diminishes over time, but remains positive in the last year (0.4 percentage points);
Actual growth from 1993.4 to 1994.3 is -4.6 percent, while the model predicts essentially zero growth. This large positive prediction error may be the reverse side of the large negative prediction errors in the previous four years; i.e., the same factor may explain both. Based on the plotted actual and simulated series (Exhibit 6.6), the reversal in the sign of the prediction error for caseload growth actually occurs in the first half of 1993.
UP Caseload
Florida was one of many states that did not have an UP program for the full sample period, and we have not used the findings from the UP models to simulate its caseload experience over the period of its existence.
Exhibit 6.6
Actual and Predicted Caseload for Florida, 1979.4 - 1994.3
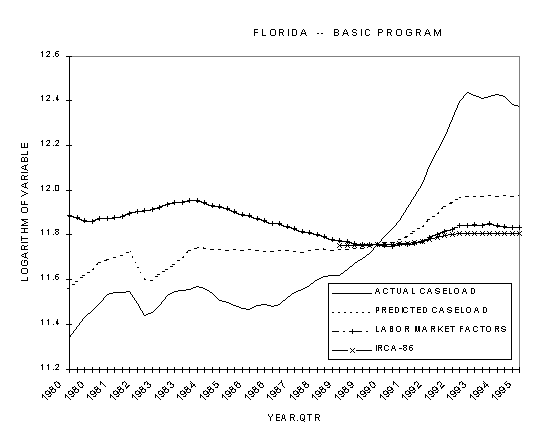
Average Monthly Benefits
The average annual decline in AMB in Florida over the period (exhibit 6.5, bottom section) was less than for the nation (0.6 percent per year vs. 2.0 percent). The model predicts an increase of 0.8 percent per year, implying an unaccounted for decline of 1.4 percentage points per year -- close to the value for the nation. As in California, the pattern of changes predicted by the model is similar to that for the nation. The most substantial difference is that the AFDC benefit variables predict a much larger increase in AMB during the first three-year subperiod (3.2 percentage points per year vs. 1.1 percentage points for the nation).
3. Maryland
Basic Caseload
In contrast to California and Florida, Maryland experienced average Basic caseload growth that was substantially below the national average over the whole period (0.5 percent per year vs. 2.2 percent nationally). The model predicts growth that is just a tenth of a percentage point higher (Exhibit 6.7, top section). Patterns of growth predicted by the state-level variables and federal legislation dummies in the model are remarkably similar to the patterns observed for the nation as a whole (Exhibit 6.1).
| Exhibit 6.7 | ||||||||
| Decomposition of Maryland Caseload and Average Monthly Benefit Series | ||||||||
| Average Annual Growth Rate | Annual Growth Rate Accounted for by: | |||||||
| Program, Period, and Model | Actual | Accounted for by Model | Not Accounted for by Model | Population Growth and Aging | Vital Statistics Variables | Labor Market Variables | AFDC Benefits | Other Variables |
| Basic | ||||||||
| 1979.4 - 1983.3 | -1.6% | -0.2% | -1.4% | 2.2% | 0.6% | 1.2% | -4.4% | 0.2% |
| 1983.4 - 1989.3 | -1.6% | -1.5% | 0.0% | 1.5% | 0.5% | -4.0% | 0.4% | 0.1% |
| 1989.4 - 1993.3 | 5.6% | 4.4% | 1.2% | -0.1% | 0.2% | 3.8% | -0.2% | 0.7% |
| 1993.4 - 1994.3 | 1.1% | 1.0% | 0.0% | -0.6% | 0.7% | -0.6% | 1.3% | 0.2% |
| 1979.4 - 1994.3 | 0.5% | 0.6% | -0.1% | 1.1% | 0.5% | -0.3% | -1.0% | 0.3% |
| Unemployed Parent 1 | ||||||||
| 1979.4 - 1983.3 | 13.2% | 5.4% | 7.8% | 2.1% | n.a. | 7.8% | -4.5% | n.a. |
| 1983.4 - 1989.3 | -18.4% | -14.6% | -3.8% | 2.0% | n.a. | -16.9% | 0.3% | n.a. |
| 1989.4 - 1993.3 | 12.1% | 18.8% | -6.7% | 0.6% | n.a. | 18.8% | -0.5% | n.a. |
| 1993.4 - 1994.3 | -15.1% | -7.9% | -7.2% | 0.2% | n.a. | -7.7% | -0.4% | n.a. |
| 1979.4 - 1994.3 | -1.6% | 0.1% | -1.7% | 1.5% | n.a. | -0.2% | -1.3% | n.a. |
| Average Monthly Benefit | ||||||||
| 1980.4 - 1983.3 | -3.4% | 2.0% | -5.3% | n.a. | 0.5% | -0.1% | 1.5% | 0.1% |
| 1983.4 - 1989.3 | 2.1% | 1.2% | 0.9% | n.a. | 0.4% | 0.0% | 0.9% | -0.1% |
| 1989.4 - 1993.3 | -6.5% | -3.4% | -3.1% | n.a. | 0.0% | -0.3% | -3.2% | 0.0% |
| 1980.4 - 1993.3 | -1.8% | 0.0% | -1.8% | n.a. | 0.3% | -0.1% | -0.2% | 0.0% |
| 1. The UP caseload model does not include the vital statistic variables and the AMB model does not include a variable for population growth and aging. | ||||||||
One distinct difference is that the labor market variables have a much larger estimated impact in Maryland during the 1989.4 - 1993.3 period than for the country as a whole (3.8 percentage points per year vs. 1.5 nationally), while they have a relatively smaller estimated impact in the 1979.4 - 1983.3 period (1.2 percentage points per year vs. 2.1 nationally). Overall, the predicted series tracks the actual series for Maryland quite closely (Exhibit 6.8, top panel).
UP Caseload
Maryland's UP caseload declined over the entire sample period, at an average annual rate of 1.6 percent (Exhibit 6.7, middle section), while the model predicts essentially no change. According to the model, the only factor contributing substantially to the decline is reductions in AFDC benefits, accounting for average annual decline of 1.3 percentage points -- about the same as for the national UP caseload. The model underpredicts growth somewhat during the first four-year subperiod of the sample, underpredicts the decline in the second five-year subperiod, and overpredicts the growth in the third four-year subperiod. In the last year of the sample, the UP caseload declines by almost twice as much (15.1 percent) as the model predicts (7.9 percent). It appears from the plot of the actual and predicted series (Exhibit 6.8, bottom panel) that the model predicts an earlier impact of economic recovery after the 1981-82 recession than actually occurred, but a later impact of recovery after the 1990-91 recession than actually occurred.
Steven Thompson reviewed our findings for Maryland and affirmed that the model provides a reasonably accurate explanation of the behavior of Maryland's caseloads.(8) He thinks that the main reason Maryland's caseload growth over the full period was less than the national average was relatively strong employment growth; from 1980 to 1990 non-agricultural employment and per capita personal income grew at a rate that was almost 50 percent higher than the national average. He also pointed out that the larger impact of the recent recession for Maryland was related to substantial cutbacks in federal spending, a major source of employment in Maryland.
Thompson has developed for Maryland the most advanced time-series model of state caseloads that we have seen. He recently has developed a version of the model with asymmetries in business cycle effects that fits Maryland's experience well, with the effects of recessions on caseload growth being substantially larger and more immediate than effects of recoveries on caseload decline. Although the pooled model tracks Maryland's experience fairly well, introducing asymmetric business cycle effects might substantially improve the fit.
Exhibit 6.8
Actual and Predicted Caseloads for Maryland, 1979.4 - 1994.3
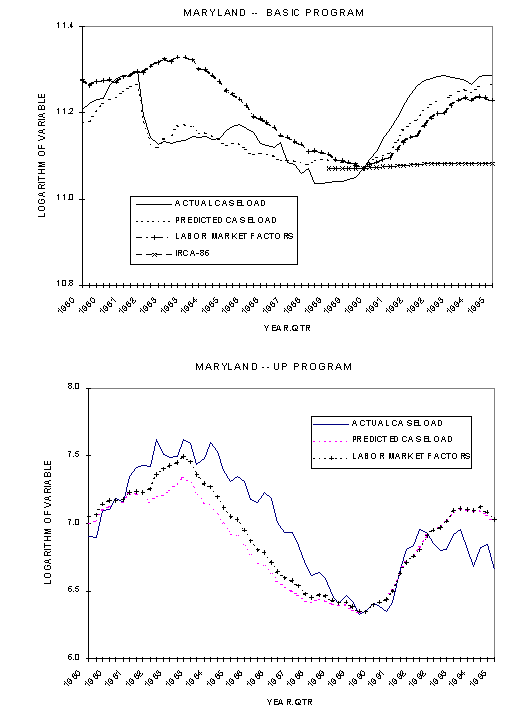
Average Monthly Benefits
The AMB simulation findings for Maryland (bottom section of Exhibit 6.7) are very similar to those for the nation. The average annual rate of decline of AMB during the whole period was 1.8 percent, vs. 2.0 for the nation, and in both cases the model predicts essentially no change. The estimated positive effects of benefit changes captured by the model during the first three-year subperiod are about the same as for the nation. As in California, AMB declined in the last four-year subperiod by substantially more than for the nation (6.5 percent per year vs. 4.1 percent) and the benefit variables account for more decline (3.2 percentage points per year vs. 1.9 percentage points).
4. Wisconsin
Basic Caseload
Wisconsin's Basic caseload at the end of the period was essentially the same as at the beginning, but this masks some sharp changes in the series within the period. According to Tom Corbett, episodes for Wisconsin's caseload differ in timing from the subperiods selected for the simulation analysis (Exhibit 6.9):(9)
- From 1979 through 1985 Wisconsin experienced severe economic difficulties and also had a very generous welfare system relative to other states. The caseload peak in 1986 was a result of these combined factors;
- From 1986 through 1991, approximately, and especially from 1987 to 1989, Wisconsin's export-sensitive economy boomed, in part driven by the decline in the value of the dollar, and welfare benefits were "slashed;"
- After 1991 the decline stalled, as the economy weakened, but then continued as the economy recovered and plethora of programmatic changes were implemented.
The welfare cuts in the middle period were partly in the form of lower maximum monthly benefits, which are captured in the model, and, to a lesser extent, a change in attitude in welfare offices. Cultural change in the welfare system has apparently been a more significant factor recently. Corbett writes that "guarantee levels [i.e., MMB] and benefit reduction rates are being swamped in importance by aggressive client diversion programs and aggressive changes in agency mission and modes of operation."
| Exhibit 6.9 | ||||||||
| Decomposition of Wisconsin Caseload and Average Monthly Benefit Series | ||||||||
| Average Annual Growth Rate | Annual Growth Rate Accounted for by: | |||||||
| Program, Period, and Model | Actual | Accounted for by Model | Not Accounted for by Model | Population Growth and Aging | Vital Statistics Variables | Labor Market Variables | AFDC Benefits | Other Variables |
| Basic | ||||||||
| 1979.4 - 1983.3 | 1.1% | 0.4% | 0.6% | 0.9% | 0.4% | 3.1% | -4.2% | 0.1% |
| 1983.4 - 1989.3 | -0.4% | -3.5% | 3.1% | -0.1% | 0.6% | -4.0% | -0.2% | 0.1% |
| 1989.4 - 1993.3 | 0.2% | 0.2% | 0.0% | 0.0% | 0.7% | -0.7% | 0.0% | 0.3% |
| 1993.4 - 1994.3 | -3.2% | 0.3% | -3.5% | -0.7% | 0.3% | -0.4% | 1.0% | 0.1% |
| 1979.4 - 1994.3 | 0.0% | -1.2% | 1.2% | 0.2% | 0.5% | -1.0% | -1.1% | 0.1% |
| Unemployed Parent 1 | ||||||||
| 1979.4 - 1983.3 | 46.6% | 19.4% | 27.1% | 0.8% | n.a. | 22.8% | -4.2% | n.a. |
| 1983.4 - 1989.3 | -12.2% | -19.3% | 7.0% | 0.3% | n.a. | -19.2% | -0.4% | n.a. |
| 1989.4 - 1993.3 | -2.2% | 0.6% | -2.8% | 0.9% | n.a. | 0.0% | -0.3% | n.a. |
| 1993.4 - 1994.3 | -18.6% | -3.7% | -14.9% | 0.2% | n.a. | -3.2% | -0.7% | n.a. |
| 1979.4 - 1994.3 | 5.7% | -2.6% | 8.3% | 0.6% | n.a. | -1.8% | -1.4% | n.a. |
| Average Monthly Benefit | ||||||||
| 1980.4 - 1983.3 | -0.6% | 2.0% | -2.6% | n.a. | 0.3% | -0.7% | 2.7% | -0.3% |
| 1983.4 - 1989.3 | -3.2% | -1.2% | -2.0% | n.a. | 0.4% | 0.2% | -1.9% | 0.0% |
| 1989.4 - 1993.3 | -1.6% | -1.9% | 0.3% | n.a. | 0.3% | -0.3% | -1.8% | 0.0% |
| 1980.4 - 1993.3 | -2.1% | -0.7% | -1.4% | n.a. | 0.4% | -0.2% | -0.8% | -0.1% |
| 1. The UP caseload model does not include the vital statistic variables and the AMB model does not include a variable for population growth and aging. | ||||||||
The model simulations largely support Corbett's comments and provide some additional insights. According to the model, the strength of Wisconsin's labor market reduced Basic caseload growth by an average of 4.0 percentage points per year from 1983.4 to 1989.4, whereas the improving national labor market reduced nation growth by only 3.3 percentage points. In the following period, through 1993.3, the economy contributed, on average, -0.7 percentage points per year to Wisconsin's caseload growth, compared to 1.5 percentage points for the nation. In the last year of the sample, however, the recovery of the national economy has had a somewhat larger effect on the nation's caseload than on growth in Wisconsin (-0.8 percentage points for the nation vs. -0.4 percentage points for Wisconsin).(10)
The analysis also finds that changes in program parameters have slowed growth in Wisconsin's caseload relative to that of the rest of the country since 1983.4, but the importance of these changes appears secondary to strong economic performance. From 1983.4 to 1989.3, program parameter changes contributed, on average, -0.2 percentage points per year to Wisconsin's caseload growth compared to positive 0.2 percentage points for the nation. From 1989.4 to 1993.3 the difference was small -- 0.0 percentage points for Wisconsin vs. 0.1 percentage points for the nation. In the last year these made a positive contribution to Wisconsin's caseload growth of 1.0 percentage points, according to the model. As explained previously, this is attributed to the expansion of the EITC, and the estimated effect for the nation is even larger, 1.3 percent.
The effects of welfare reforms in Wisconsin may have been substantially greater than the effects that are captured in the model, however. As Corbett points out, the many changes that have occurred are not captured in the key program parameters. The decline in the caseload in the last year of the sample, which is not explained by the model, is especially noteworthy. The actual caseload declined by 3.2 percent in 1993.4 - 1994.3, while the model predicts an increase of 0.3 percent. Corbett and others have attributed much of the recent decline to Wisconsin's aggressive efforts to encourage employment and discourage long-term dependency (see Mead, 1996, and Wiseman, 1996). Our findings are largely consistent with that interpretation for 1994, but factors in the model account for all of Wisconsin's low caseload growth in the previous four years. In fact, from 1987 to 1993 the predicted caseload series tracks the actual series very well (Exhibit 6.10).
The simulations point to two other factors that have contributed to low caseload growth in Wisconsin relative to the nation. First, population growth and aging have contributed less to caseload growth in Wisconsin than in the nation -- 0.2 percentage points per year on average over the entire sample period, vs. 0.8 percentage points for the country. In the last year of the sample, the contribution of this factor in Wisconsin is estimated at -0.7 percentage points, vs. -0.4 percentage points for the country. Second, IRCA legalizations had a much smaller estimated impact in Wisconsin than in other states. This is reflected in the estimated contribution of "other factors" for the period from 1989.4 to 1993.3; the contribution of these factors in Wisconsin is an average 0.3 percentage points per year during this period, compared to 1.7 percentages points for the nation.
Exhibit 6.10
Actual and Predicted Caseloads for Wisconsin, 1979.4 - 1994.3
UP Caseload
The Wisconsin UP caseload grew at an average annual rate of 5.7 percent over the full period, slightly lower than the national rate of growth (7.0 percent), but the model predicts an average annual decline of 2.6 percent (Exhibit 6.9, middle section). As is evident from plots of the predicted and actual series (Exhibit 6.10, bottom panel), most of the positive prediction error comes from the 1979.4 - 1983.3 period when actual growth occurred at an average annual rate of 46.6 percent, compared to predicted growth of 19.4 percent. We do not have an explanation for this exceptionally high rate of growth. Like in California, the model predicts a larger caseload decline than actually occurred in the following five-year subperiod. During the next four years the caseload declines by an average of 2.2 percent per year when the model predicts growth of 0.6 percent, and during the final year of the sample the caseload declines by 18.6 percent while the model predicts a decline of only 3.7 percent. While these larger than expected declines may be due to Wisconsin's work-oriented welfare reforms, the size of the prediction errors that occur in the earlier part of the sample period suggest that this conclusion may be premature.
Average Monthly Benefits
The AMB simulation findings for Wisconsin (bottom section of Exhibit 6.9) depart from those for the nation and the three other states in some interesting ways. While the average annual decline for the full period is about the same as for the nation (2.1 percent per year vs. 2.0 percent), much of the decline occurred in the middle four-year period, the period during which the state began to cut its benefits; most of the decline for the nation and the other states occurred in the first and last subperiods. In Wisconsin, benefit changes captured by the model had a substantial positive impact during the first three-year subperiod (2.7 percentage points per year) and substantial negative impacts in the middle and last four-year subperiods (-1.9 and -1.8 percentage points per year, respectively).
D. SUMMARY AND DISCUSSION
1. Basic Caseload
The model provides several insights into the cycles in caseload growth during the sample period:
- For the nation as a whole, and in all states examined, we found that the slow growth of the 1979.4 - 1983.3 period was the net result of substantial offsetting forces: the growth and aging of the population and the double-dip recession on the positive side, and the substantial cuts in AFDC benefits resulting from OBRA81 on the negative side. The impact of the OBRA81 cuts is all the more impressive when it is recognized that the recession would have caused substantial additional caseload growth in its absence. We estimate that the total effect of these cuts was on the order of 20 percent. The size of the estimated impact from these cuts vary little across the four states we examined.
- For the nation as a whole, and in all states, we found that the influence of population growth and aging declined substantially over the period. That is, slower growth and, eventually, a decline in the size of the population most at-risk for AFDC family headship was a strong force working against accelerating growth during this period, making the caseload growth in the latter part of the period all the more striking.
- The Immigration Reform and Control Act of 1986 eventually led to substantial caseload growth in at least some states, including California and, to a lesser extent, Florida, as illegal residents were legalized. Even though newly legalized parents were not eligible for benefits immediately, their U.S. born children were if other eligibility criteria were satisfied.
- Most of the growth not accounted for by the state variables and federal legislation dummies in the model occurred between 1984 and 1992. The divergence between the actual and predicted series for Florida from 1987 to 1992 is especially striking. Possible reasons for the missed growth during this period include:
Effects of federal legislation that are captured by the coefficients of the calendar dummies in the regression model, but not included in the predicted series. This almost surely explains part of the growth, but how much is difficult to determine. It would certainly not explain the very high growth not accounted for in Florida;
Overestimation of the impact of the recovery from 1983 to 1989, and underestimation of the impact of the recession of 1990-91. It could be that characteristics of the recessions that are not captured in the model's variables explain exceptionally high growth in some states (as per Don Winstead's comments on Florida);
Underestimation of the contribution of immigration. We have not looked at the effects of legal immigration after the three-year waiting period, nor have we modeled the effects of refugees, whom we understand are a high participant group;
Underestimation of the role of changes in household characteristics -- especially the growth in female headed households -- CBO (1993) attributed much of the Basic caseload growth in the 1989 - 1992 period to this factor in their time-series analysis. We could not satisfactorily measure female headed households at the state level, and found that vital statistics variables played a less substantial role in predicting growth during this period;
Increases in the cost of health care and reductions in access to health insurance -- substantial efforts to capture these factors in the model were not very successful. Given the evidence of the importance of these factors from micro data analyses, however, we still believe they may have been important. Don Winstead's comments concerning Medicaid outreach efforts in Florida suggest that unmeasured Medicaid factors could be an important factor in some states. In previous studies of SSI applications and awards, we have found substantial evidence of similar effects in other states for SSI, but also have not been able to quantify them (Lewin-VHI, 1995b, 1995c, and 1995d); and
Declines in job prospects for low-skilled workers that are not reflected in the unemployment rate and/or the trade employment variable. This explanation of the growth not accounted for by the model over the entire period was favored by several welfare researchers when preliminary findings from this project were presented at a recent conference.
2. Unemployed Parent Caseload
The model also provides important insights concerning past cycles in the UP caseload:
- While labor market factors fall short of explaining all of the large caseload growth observed during the two major recessions of this period, they do explain much of it -- especially for the 1990-91 recession.
- The estimated impact of the OBRA81 cuts on the UP caseload is proportionately as large as the impact on the Basic caseload, even though the national UP caseload continued to rise after OBRA81 was implemented. The continued rise in the UP caseload is largely explained by the recession.
- As with the Basic caseload, we found that the influence of population growth and aging declined substantially over the period.
- We could not find any measurable impact of legalizations under the Immigration Reform and Control Act of 1986 on the UP caseload, which may be because most child-only cases are in the Basic program. Note, however, that when we re-estimated the model using a method that gave more weight to large states (Exhibit 5.3), along with some other specification changes, the coefficient of the IRCA variable became statistically significant. Hence, it may be inappropriate to conclude that there was no effect on the UP caseload.
- Much of the caseload growth not accounted for by the variables in the model occurred in the first two years of the sample, both nationally and in the three states with UP programs for the entire period -- especially Wisconsin. This differs from what we found for the Basic caseload. We also found substantial growth not accounted for between 1984 and 1989, although in Maryland we found that the caseload decline in this period was greater than that predicted by the model. These patterns suggest that the unidentified factors at work may be different than those for the Basic caseload.
3. Average Monthly Benefits
The model predicts very little change in AMB over the period in all states, yet there was a substantial decline. Particularly anomalous is the model's prediction of an increase due to changes in benefit variables in the first three-year subperiod, when a substantial decline actually occurred. While effects of OBRA81 that are captured by the year dummies and not included in the simulation may explain part of the anomaly, the largest negative coefficient on a year dummy is for the previous year. We have devoted relatively little effort to development of the AMB model, and it may be that additional effort would resolve this anomaly.
4. Conclusion
The simulations demonstrate the ability of a pooled analysis to provide insights into the causes of caseload growth. Drawing on the experiences of all states, as the model does, and comparing simulations for individual states to national simulations using a single model, provides information about caseload growth in individual states that might easily be missed in an individual state time-series analysis.
At the same time, however, the simulations for individual states demonstrate limitations of the model, at least as currently constructed. Most of these limitations stem from measurement problems -- factors thought by many to be important determinants of caseload growth at the state level are not adequately measured at the state level. Some improvements can be made in this area, as outlined in Chapter 1, and we expect that making these improvements would add significantly to the model's ability to capture the determinants of caseload growth. One factor that will become increasingly important as we move forward, and that will be especially difficult to measure, is the many detailed and varied changes that states are currently making to their welfare programs.
Other changes to the model might also make it substantially more powerful. Given the interaction between the Basic and UP programs that is known in California, exploring ways to model this interaction might be fruitful. Alternatively, it may be better to simply combine the caseloads and model them together. As Michael Wiseman has pointed out, the big issue is whether or not a mother and her children end up on welfare, not whether there is a second parent in the household.(11) This would also solve the specification problem that arises because of the absence of the UP program in many states for a significant part of the sample.(12) The findings for individual states and the comments on them also suggest that efforts to disaggregate the caseload by characteristics such as race/ethnicity and citizenship would be very useful. It might also be useful to divide the largest states into sub-state areas for the analysis, such as Dade County vs. the rest of Florida and northern vs. southern California.(13) Further consideration of asymmetries in business cycle effects also seems warranted. A number of other ideas have been suggested by reviewers of the model, as discussed at the end of Chapter 1.
Improvements to the model would likely increase the extent to which the state-level factors in the model and dummy variables for federal program changes account for growth and cyclical variation in the national time series. It would be a mistake, however, to focus exclusively on improving the fit of the national series. Significant gains in understanding caseload growth are more likely to be achieved if future efforts focus on the fundamental measurement and structural issues rather than goodness of fit per se. That has been our approach, and we think it has been very worthwhile. The strength of our findings, especially concerning business cycle effects and program changes, have impressed the many experts in welfare research who have reviewed our work and have convinced us that further efforts to improve the model would be rewarding.
Notes
1. The calendar year dummies reflect growth not accounted for by the explanatory variables. The quarterly dummies do not play a role in the simulations because the number of quarters in the full period, and each subperiod, is a multiple of four.
2. Each of the two recessionary periods includes approximately one year following the end of the official recession, during which the economy continues to be sluggish.
3. The vertical distance between a point on the labor market line corresponding to a specific quarter and the point corresponding to 1989.4 is the estimated contribution of labor market strength to the caseload for that quarter relative to labor market strength for 1989.4. An analogous interpretation applies to the IRCA series. The IRCA series begins in 1988.1, the first quarter in which there were legalizations under IRCA.
4. For the Basic caseload, growth not accounted for is 1.8 percent, and for the UP caseload in the 19 states it is 6.1 percent. Because the UP caseload is a very small share of the total caseload, total caseload growth not accounted for is only slightly above the 1.8 percent figure -- very close to 2.0.
5. "National" estimates refer only to the 19 states with UP programs for the entire sample period.
6. Personal correspondence, October 1996.
7. Personal correspondence, October 22, 1996.
8. Personal correspondence, October 22, 1996.
9. Personal correspondence, November 4, 1996.
10. Wiseman (1996) also concludes that economic growth has had a greater impact on the national caseload than on the Wisconsin case load in the last two years.
11. Personal correspondence, October 1996.
12. This is the approach taken by Cromwell et al. (1986), although the participation measure was Medicare AFDC enrollees, not the AFDC caseload.
13. Steven Thompson has developed a separate time-series model for Prince George's County because the behavior of the caseload in that county is differs substantially from the behavior of the caseload in the rest of the state.
REFERENCES
Bane, Mary Jo and David T. Ellwood. (1994) Welfare Realities: From Rhetoric to Reform. Cambridge and London: Harvard University Press.
Barnow, Burt S. (1988) Developing Models to Predict State AFDC Caseloads: A Guide for States. (HHS Contract No. HHS-100-86-0051) Washington, D.C.: Report to the Office of the Assistant Secretary for Planning and Evaluation, U.S. Department of Health and Human Services.
Blank, Rebecca M. (1988) "The Effect of Medical Need and Medicaid on AFDC Participation." Journal of Human Resources, 24(1), 54-87.
Blank, Rebecca M. and Patricia Ruggles. (1996) "When do Women Use Aid to Families with Dependent Children and Food Stamps?: The Dynamics of Eligibility versus Participation." Journal of Human Resources, 31(1), 57-87.
Burkhauser, Richard V., Kenneth A. Couch and David C. Wittenburg (1996), "The Effect of 1990 and 1991 Federal Minimum Wage Increases on Younger "At-Rick" Workers," Working Paper, Center for Policy Research, Syracuse University
Committee on Ways and Means, U.S. House of Representatives. (1994) Overview of Entitlement Programs: 1994 Green Book. Washington, D.C.: U.S. Government Printing Office.
Congressional Budget Office, Immigration and Welfare Reform. CBO Papers, February 1995.
Congressional Budget Office, Forecasting AFDC Caseloads, with an Emphasis on Economic Factors. CBO Staff Memorandum, July 1993.
Congressional Budget Office, A Preliminary Analysis of Growing Caseloads in AFDC.. CBO Staff Memorandum, December 1991.
Cromwell, Jerry, et al. (1986) "Impacts of Economic and Programmatic Changes on Medicaid Enrollments." The Review of Economics and Statistics, 232-240.
Currie, Janet, Lucia Nixon, and Nancy Cole. (1996) "Restrictions on Medicaid Funding of Abortion." The Journal of Human Resources, 31(1): 159-188.
Danziger, Sheldon, Haveman, Robert, and Plotnick, Robert. (1981) "How Income Transfers Affect Work, Savings, and the Income Distribution: A Critical Review." Journal of Economic Literature, 19(3), 975-1028.
Fitzgerald, John. (1991) "Welfare Durations and the Marriage Market: Evidence from the Survey of Income and Program Participation." Journal of Human Resources, 26(3), 545-561.
Fraker, Thomas, Robert Moffitt, and Douglas Wolf. (1985) Effective Tax Rates and Guarantees in the AFDC Program, 1967-1982. Journal of Human Resources, 20(4): 264-277.
Gabe, Thomas. (1992) Demographic Trends Affecting Aid to Families with Dependent Children (AFDC) Caseload Growth. Washington, D.C.: The Congressional Research Service, The Library of Congress.
Garasky, Steven. (1990) "Analyzing the Effect of Massachusetts' ET Choice Program on the State's AFDC-Basic Caseload." Evaluation Review, 14(6), 701-710.
Gaylin, Daniel S. and Sara S. McLanahan. (1995) "Will Child Support Enforcement Reduce Nonmarital Childbearing?" Working Paper, Princeton University.
Garrett, A. Bowen and Sherry Glied (1997) "The Effect of U.S. Supreme Court Ruling Sullivan v. Zebley on Child SSI and AFDC Enrollment: A Natural Experiment," Working Paper. School of Public Health, University of California, Berkley
General Accounting Office. (1996) Welfare Waivers Implementation: States Work to Change Welfare Culture, Community Involvement, and Service Delivery. GAO/HEHS 96-105, Washington, D.C.: GAO, July.
Gritz, R. Mark, and Thomas McCurdy. (1991) "Patterns of Welfare Utilization and Multiple Program Participation among Young Women." Stanford University, Stanford, California.
Grossman, Jean Baldwin. (1985) A Forecasting System for AFDC Caseloads and Costs. (HHS Contract No. 600-82-0097) Report to the Office of Family Assistance, Social Security Administration, U.S. Department of Health and Human Services. Washington, D.C.: Mathematica Policy Research, Inc.
Gruber, Jonathan and Jeffery D. Kubik. (1994) "Disability Insurance Rejection Rates and the Labor Supply of Older Workers." (Working Paper No. 4941) Cambridge, Massachusetts: National Bureau of Economic Research.
Haas-Wilson, Deborah. (1996) "The Impact of State Abortion Restrictions on Minors' Demand for Abortions." The Journal of Human Resources, 31(1), Winter: 140-158.
Hoynes, Hillary W. (1996) "Local Labor Markets and Welfare Spells: Do Demand Conditions Matter?" Working Paper, Department of Economics, University of California at Berkeley.
Hoynes, Hillary W., and Thomas McCurdy. (1994) "Has the Decline in Benefits Shortened Welfare Spells?" American Economic Review, 84(2).
Lewin-VHI, Inc. (1995a) Determinants of AFDC Caseload Growth: Literature Review. Draft Report to the Assistant Secretary for Planning and Evaluation in the Department of Health and Human Services and the Social Security Administration, December 20.
Lewin-VHI, Inc. (1995b) Labor Market Conditions, Socioeconomic Factors, and the Growth of Applications and Awards for SSDI and SSI. Final Report to the Assistant Secretary for Planning and Evaluation in the Department of Health and Human Services and the Social Security Administration, May 23.
Lewin-VHI, Inc. (1995c) Longer Term Factors Affecting Disability Program Applications and Awards. Report to the Assistant Secretary of Planning and Evaluation in the U.S. Department of Health and Human Services and the Social Security Administration, October 31.
Lewin-VHI, Inc. (1995d) Case Studies of State-level Factors Contributing to DI and SSI Disability Application and Award Growth. Report to the Assistant Secretary of Planning and Evaluation in the U.S. Department of Health and Human Services and the Social Security Administration, December 5.
Lewin-VHI, Inc. (1996) Determinants of AFDC Caseload Growth: Analysis Plan. Report to the Assistant Secretary for Planning and Evaluation in the Department of Health and Human Services and the Social Security Administration, April 24.
McKinnish, T., S. Sanders, and J. Smith. (1995) "Estimates of Effective Guarantees and Tax Rates in the AFDC Program for the Post-OBRA Period," Department of Economics, Carnegie-Mellon University.
Mead, Lawrence (1996) "The Decline of Welfare in Wisconsin." Wisconsin Policy Research Institute Report, 9(3), March, 1-44.
Merz, Jon F., Catherine A. Jackson, Catherine A., and Klerman, Jacob A. (1995) "A Review of Abortion Policy: Legality, Medicaid Funding, and Parental Involvement, 1967-1994." Women's Rights Law Reporter, Winter 1995, 17(1).
Moffitt, Robert. (1985) Work Incentives in Transfer Programs (Revisited). (Discussion Paper No. 787-86) Madison, Wisconsin: Institute for Research on Poverty, University of Wisconsin-Madison.
Moffitt, Robert. (1986) Trends in AFDC Participation over Time: Evidence on Structural Change. (Special Report No. 41) Madison, Wisconsin: Institute for Research on Poverty, University of Wisconsin-Madison.
Moffitt, Robert and Barbara Wolfe. (1992) "The Effect of the Medicaid Program on Welfare Participation and Labor Supply." The Review of Economics and Statistics 74(4), 615-626.
Moffitt, Robert. (1992) "Incentive Effects of the U.S. Welfare System: A Review." Journal of Economic Literature, 30, March 1992, 1-61.
Moffitt, Robert. (1994) "Welfare Effects on Female Headship with Area Effects." Journal of Human Resources, 29(2), 621-636.
Office of Family Assistance, Administration for Children and Families. (1991) Characteristics of State Plans for Aid to Families with Dependent Children, 1990-91 Edition. U.S. Department of Health and Human Services: Washington, DC.
Office of Family Assistance, Administration for Children and Families. (1995). Overview of the AFDC Program, Fiscal Year 1994. U.S. Department of Health and Human Services: Washington, DC.
Office of Family Assistance, Administration for Children and Families. (various years) Quarterly Public Assistance Statistics. U.S. Department of Health and Human Services: Washington, DC.
Oregon State Department of Human Resources. (1990) AFDC Caseload Forecasting Techniques and Processes: A Fifty State Survey. Adult and Family Services Division.
Parks, R.W. (1967) "Efficient Estimation of a System of Regression Equations When Disturbances Are Both Serially and Contemporaneously Correlated." Journal of the American Statistical Association, 62, 500-509.
Parsons, Donald. (1991) "Self-Screening in Targeted Public Transfer Programs," Journal of Political Economy, 99(4), 859-876.
Pavetti, LaDonna A. (1993) The Dynamics of Welfare and Work: Exploring the Process by Which Women Work Their Way off Welfare. Dissertation, Harvard University, Cambridge, MA.
Regional Economic Studies Institute (1994), Quarterly Forecast of the AFDC Caseload in Maryland, FY 1994 - FY 1996. RESI, Towson State University, Towson, MD.
SAS Institute Inc. SAS/ETS® User's Guide, Version 6, Second Edition. Cary, NC: SAS Institute Inc., 1993.
Shroder, M. (1995) "Games the States Don't Play: Welfare Benefits and the Theory of Fiscal Federalism." The Review of Economics and Statistics, 77(1), 183-191.
Tobin, James. (1994) "Poverty in Relation to Macroeconomic Trends, Cycles, and Policies." In Dansziger, S.H., G.D. Sandefur, and D.H. Weinberg (editors), Confronting Poverty: Prescriptions for Change. Cambridge, MA: Harvard University Press, 147-167.
Wiseman, Michael. (1996) "State Strategies for Welfare Reform: The Wisconsin Story," Journal of Policy Analysis and Management, 15(4), 515-46.
Wissoker, Douglas A. and Harold W. Watts (1994) The Impact of FIP on AFDC Caseloads. Report to the Washington State Legislative Budget Committee. Washington D.C.: The Urban Institute, June.
Yelowitz, Aaron S. (1993) "The Medicaid Notch, Labor Supply, and Welfare Participation: Evidence from Eligibility Expansions." Department of Economics, University of California at Los Angeles.
APPENDIX A
VARIABLE DEFINITIONS(1)
| Dependent Variables |
| Variable | Description | Data | Construction | Dates |
| BCASEL | Natural log of average monthly AFDC-Basic caseload during given quarter. | Monthly caseload data appear in the Administration for Children and Families (ACF) publications, Quarterly Public Assistance Statistics (1981-1993) and Public Assistance Statistics (1978-1980). Most data obtained electronically from ACF. | Quarterly values constructed from monthly data (1/78-3/95) using SAS/ETS PROC EXPAND with observed=average and method=aggregate options. | 1978.4 - 1995.1 |
| UCASEL | Natural log of average monthly AFDC-UP caseload during given quarter. | Monthly caseload data appear in the Administration for Children and Families (ACF) publications, Quarterly Public Assistance Statistics (1981-1993) and Public Assistance Statistics (1978-1980). Most data obtained electronically from ACF. | Quarterly values constructed from monthly data (1/78-3/95) using SAS/ETS PROC EXPAND with observed=average and method=aggregate options. | 1978.4 - 1995.1 |
| BRTOTL | Natural log of average monthly AFDC-Basic total recipients during given quarter. | Monthly recipient data (10/82-3/95) appear in the Administration for Children and Families (ACF) publications, Quarterly Public Assistance Statistics (1981-1993). Most data obtained electronically from ACF. Data prior to 10/82 were extracted from database assembled by Grossman (1985) and provided by Gilbert Crouse, ASPE. | Quarterly values constructed from monthly data (1/78-3/95) using SAS/ETS PROC EXPAND with observed=average and method=aggregate options. | 1978.1 - 1995.1 |
| URTOTL | Natural log of average monthly AFDC-UP total recipients during given quarter. | Monthly recipient data (10/82-3/95) appear in the Administration for Children and Families (ACF) publications, Quarterly Public Assistance Statistics (1981-1993). Most data obtained electronically from ACF. Data prior to 10/82 were extracted from database assembled by Grossman (1985) and provided by Gilbert Crouse, ASPE. | Quarterly values constructed from monthly data (1/78-3/95) using SAS/ETS PROC EXPAND with observed=average and method=aggregate options. | 1978.1 - 1995.1 |
| Variable | Description | Data | Construction | Dates |
| BRKIDL | Natural log of average monthly AFDC-Basic child recipients during given quarter. | Monthly recipient data appear in the Administration for Children and Families (ACF) publications, Quarterly Public Assistance Statistics (1981-1993) and Public Assistance Statistics (1978-1980). Most data obtained electronically from ACF. | Quarterly values constructed from monthly data (1/78-3/95) using SAS/ETS PROC EXPAND with observed=average and method=aggregate options. | 1978.1 - 1995.1 |
| URKIDL | Natural log of average monthly AFDC-UP child recipients during given quarter. | Monthly recipient data appear in the Administration for Children and Families (ACF) publications, Quarterly Public Assistance Statistics (1981-1993) and Public Assistance Statistics (1978-1980). Most data obtained electronically from ACF. | Quarterly values constructed from monthly data (1/78-3/95) using SAS/ETS PROC EXPAND with observed=average and method=aggregate options. | 1978.1 - 1995.1 |
| AMB | Natural log of average monthly AFDC payment per family during given quarter (1990 dollars). | Average monthly benefit data obtained from the Administration for Children and Families (ACF) publications, Quarterly Public Assistance Statistics (1981-1993) and Public Assistance Statistics (1978-1980). | When reported, quarterly values were imported directly into the database. When only monthly values were available, a quarterly average was constructed from the monthly values. Series deflated using the regional CPI-U (1990=100). | 1980.1-1993.4 |
| Variable | Description | Data | Construction | Dates |
| Population Characteristics |
| EXPTBA | Natural log of expected average monthly AFDC-Basic caseload during given quarter. | Data used in creation of variable:
1) Estimates from the 1990 Survey of Income and Program Participation (SIPP) for AFDC participation rates for single-parent households with children under the age of 18 by age of householder. Age-specific participation rates are measured in five year age groups. 2) National average monthly AFDC-Basic caseload data for 1990. 3) National population estimates for females over age 15 by five year age groupings for 1990. 4) Annual state population estimates for females over age 15 by five year age groupings for 1978-1994. |
Equal to the number of single-parent AFDC units in the age group as tabulated from the 1990 SIPP divided by the total number of women in the age group. A*st = a Aa90 Past, where A*st is "expected" AFDC-Basic caseload in state s and year t, Aa90 is 1990 national AFDC-Basic participation rate in age group a, and Past is the number of women in age group a, living in state s during year t. Initial age-specific participation rates were adjusted by the ratio of the actual caseload for 1990 (ACF statistics) to the estimated caseload. The annual average monthly participation series was expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=average and method=spline options. | 1978.1-1994.4 |
| EXPTUP | Natural log of expected average monthly AFDC-UP caseload during given quarter. | Data used in creation of variable:
1) Estimates from the 1990 Survey of Income and Program Participation (SIPP) for AFDC participation rates for two-parent households with children under the age of 18 by age of householder. Age-specific participation rates are measured in five year age groups. 2) National average monthly AFDC-Basic caseload data for 1990. 3) National population estimates for females over age 15 by five year age groupings for 1990. 4) Annual state population estimates for females over age 15 by five year age groupings for 1978-1994. |
Equal to the number of two-parent AFDC units in the age group as tabulated from the 1990 SIPP divided by the total number of men in the age group. A*st = a Aa90 Past, where A*st is "expected" AFDC-UP caseload in state s and year t, Aa90 is 1990 national AFDC-UP participation rate in age group a, and Past is the number of men in age group a ,living in state s during year t. Initial age-specific participation rates were adjusted by the ratio of the actual caseload for 1990 (ACF statistics) to the estimated caseload. The annual average monthly participation series was expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=average and method=spline options. | 1978.1-1994.4 |
| Demographic Variables |
| Variable | Description | Data | Construction | Dates |
| Population Characteristics |
| EBATOT | Natural log of expected average monthly AFDC-Basic total recipients during given quarter. | Data used in creation of variable:
1) Estimates from the 1990 Survey of Income and Program Participation (SIPP) for AFDC participation rates for individuals living in single-parent households by age of individual. Age-specific participation rates are measured in five year age groups. 2) National average monthly AFDC-Basic total recipient data for 1990. 3) National population estimates for females over age 15 by five year age groupings for 1990. 4) Annual state population estimates for females over age 15 by five year age groupings for 1978-1994. |
Equal to the number of individuals living in single-parent AFDC units in the age group as tabulated from the 1990 SIPP divided by the total number of individuals in the age group. A*st = a Aa90 Past, where A*st is "expected" number of AFDC-Basic total recipients in state s and year t, Aa90 is 1990 national AFDC-Basic participation rate in age group a, and Past is the number of individuals in age group a, living in state s during year t. Initial age-specific participation rates were adjusted by the ratio of the actual number of total recipients for 1990 (ACF statistics) to the estimated number of total recipients. The annual average monthly participation series is expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=average and method=spline options. | 1978.1-1994.4 |
| EUPTOT | Natural log of expected average monthly AFDC-UP total recipients during given quarter. | Data used in creation of variable:
1) Estimates from the 1990 Survey of Income and Program Participation (SIPP) for AFDC participation rates for individuals living in two-parent households by age of individual. Age-specific participation rates are measured in five year age groups. 2) National average monthly AFDC-Basic caseload data for 1990. 3) National population estimates for females over age 15 by five year age groupings for 1990. 4) Annual state population estimates for females over age 15 by five year age groupings for 1978-1994. |
Equal to the number of individuals living in two-parent AFDC units in the age group as tabulated from the 1990 SIPP divided by the total number of individuals in the age group. A*st = a Aa90 Past, where A*st is "expected" AFDC-UP total recipients in state s and year t, Aa90 is 1990 national AFDC-UP participation rate in age group a, and Past is the number of individuals in age group a, living in state s during year t. Initial age-specific participation rates were adjusted by the ratio of the actual number of recipients for 1990 (ACF statistics) to the estimated number of recipients. The annual average monthly participation series is expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=average and method=spline options. | 1978.1-1994.4 |
| Demographic Variables |
| Variable | Description | Data | Construction | Dates |
| Population Characteristics |
| EBAKID | Natural log of expected average monthly AFDC-Basic child recipients during given quarter. | Data used in creation of variable:
1) Estimates from the 1990 Survey of Income and Program Participation (SIPP) for AFDC participation rates for children (under the age of 18) living in single-parent households by age of child. Age-specific participation rates are measured in five year age groups. 2) National average monthly AFDC-Basic caseload data for 1990. 3) National population estimates for females over age 15 by five year age groupings for 1990. 4) Annual state population estimates for females over age 15 by five year age groupings for 1978-1994. |
Equal to the number of children living in single-parent AFDC units in the age group as tabulated from the 1990 SIPP divided by the total number of children in the age group. A*st = a Aa90 Past, where A*st is "expected" AFDC-Basic child recipients in state s and year t, Aa90 is 1990 national AFDC-Basic participation rate in age group a, and Past is the number of children in age group a, living in state s during year t. Initial age-specific participation rates were adjusted by the ratio of the actual number of child recipients for 1990 (ACF statistics) to the estimated number of child recipients. The annual average monthly participation series is expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=average and method=spline options. | 1978.1-1994.4 |
| EUPKID | Natural log of expected average monthly AFDC-UP child recipients during given quarter. | Data used in creation of variable:
1) Estimates from the 1990 Survey of Income and Program Participation (SIPP) for AFDC participation rates for children living in two-parent households by age of child. Age-specific participation rates are measured in five year age groups. 2) National average monthly AFDC-Basic caseload data for 1990. 3) National population estimates for females over age 15 by five year age groupings for 1990. 4) Annual state population estimates for females over age 15 by five year age groupings for 1978-1994. |
Equal to the number of children living in two-parent AFDC units in the age group as tabulated from the 1990 SIPP divided by the total number of children in the age group. A*st = a Aa90 Past, where A*st is "expected" AFDC-UP child recipients in state s and year t, Aa90 is 1990 national AFDC-UP participation rate in age group a, and Past is the number of men in age group a, living in state s during year t. Initial age-specific participation rates were adjusted by the ratio of the actual number of child recipients for 1990 (ACF statistics) to the estimated number of child recipients. The annual average monthly participation series was expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=average and method=spline options. | 1978.1-1994.4 |
| Demographic Variables |
| Variable | Description | Data | Construction | Dates |
| Population Characteristics |
| FPOPxxxx, MPOPxxxx, and TPOPxxxx Variables* | Multiple state population measures by age and sex (female, male, and total), where FPOP is female population, MPOP is male population, TPOP is total population, and xxxx is the age range of the variable [e.g., FPOP2024 (females aged 20-24), MPOPLT5 (males aged 0-4), TPOPGE65 (total population 65 and over), TOTPOP (total population)]. | Various Current Population Reports and Announcements from the Population Estimates and Population Distribution Branches, Bureau of the Census, 1977-1995. Data were downloaded from Bureau of Census web page. | Annual state population data expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=middle and method=spline options. Age brackets for female, male, and total population data are: 0-4 years, 5-9 years, 10-14 years, 15-19 years, 20-24 years, 25-29 years, 30-34 years, 35-39 years, 40-44 years, 45-49 years, 50-54 years, 55-59 years, 60-64 years, 65-69 years, 70-74 years, 75-79 years, 80-84 years, and over 85 years; 16-24 years, 25-34 years, 35-44 years, 45-54 years, 55-64 years, and over 65 years. Age brackets for total population data also include: 45-64 years, 65-74 years, and over 75 years. | 1976.1-1994.4 |
| SQRTTP | Square root of state population in given quarter. | Various Current Population Reports and Announcements from the Population Estimates and Population Distribution Branches, Bureau of the Census, 1977-1995. Data were downloaded from Bureau of Census web page. | Equal to square root of TOTPOP. | 1976.1-1994.4 |
| PP4564 | State population 45 to 64 as a percent of state's population 18 and over. | Various Current Population Reports and Announcements from the Population Estimates and Population Distribution Branches, Bureau of the Census, 1977-1995. Data were downloaded from Bureau of Census web page. | Equal to TPOP4564 divided by TPOPGE18. | 1978.1-1994.4 |
| PP6574 | State population 65 to 74 as a percent of state's population 18 and over. | Various Current Population Reports and Announcements from the Population Estimates and Population Distribution Branches, Bureau of the Census, 1977-1995. Data were downloaded from Bureau of Census web page. | Equal to TPOP6574 divided by TPOPGE18. | 1978.1-1994.4 |
| Demographic Variables |
| Variable | Description | Data | Construction | Dates |
| Population Characteristics |
| PPGE75 | State population 75 and over as a percent of state's population 18 and over. | Various Current Population Reports and Announcements from the Population Estimates and Population Distribution Branches, Bureau of the Census, 1977-1995. Data were downloaded from Bureau of Census web page. | Equal to TPOPGE75 divided by TPOPGE18. | 1978.1-1994.4 |
| IMMGTOTL | Estimated total immigration by state in given quarter. | Total number of legal immigrants in given fiscal year, 1989-1994, obtained from the Immigration and Naturalization Service. Contact: Carolyn Johnson, (202) 376-6066 | Fiscal year data expanded to a quarterly series using SAS/ETS PROC EXPAND with from=year.10, observed=total, method=join, and transformout=(floor>=0) options. | 1978.1-1994.3 |
| IMMGIRCA | Estimated total number of illegal aliens legalized under the Immigration Reform and Control Act of 1986 by state in given quarter. | Illegal aliens per capita legalized under IRCA-1986 in given fiscal year, 1989-1994, obtained from the Immigration and Naturalization Service. Contact: Carolyn Johnson, (202) 376-6066 | Fiscal year data expanded to a quarterly series using SAS/ETS PROC EXPAND with from=year.10, observed=total, method=join, and transformout=(floor>=0) options. Expanded series then divided by expanded total state population. | 1989.1-1994.3 |
| Vital Statistics |
| MARRIAGE | Natural log of marriages by state in given quarter. | Annual number of marriages by state, 1978-1994, obtained from various Vital and Health Statistics publications, NCHS. | Annual values were interpolated for some years in some states when data were unavailable. Annual data are expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=total and method=spline options. | 1978.1-1994.4 |
| DIVORCE | Natural log of divorces by state in given quarter. | Annual number of divorces by state, 1978-1994, obtained from various Vital and Health Statistics publications, NCHS. | Annual values were interpolated for some years in some states when data were unavailable. Annual data are expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=total and method=spline options. | 1978.1-1994.4 |
| OOWBIRTH | Natural log of out-of-wedlock births by state in given quarter. | Annual number of out-of-wedlock by state, 1978-1994, obtained from various Vital and Health Statistics publications, NCHS. | Annual data are expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=total and method=spline options. | 1978.1-1994.4 |
| Labor Market Variables |
| Variable | Description | Data | Construction | Dates |
| UNEMPRT | Natural log of the quotient of the actual unemployment rate for given quarter divided by the expected unemployment rate for the quarter. | Data used in creation of variable:
1) Quarterly unemployment rate data by state, 1976.1-1995.4, obtained from Local Area Unemployment Statistics, Bureau of Labor Statistics. 2) National unemployment rate data by age by sex for 1990 obtained from Bureau of Labor Statistics. 3) Annual state population data by age and sex obtained from the Bureau of the Census. All data were downloaded from Internet. |
A state's expected unemployment rate in a given year is equal to the sum of the age and sex specific national unemployment rates for 1990 weighted by the ratio of the state's population in the age-sex group to the state's total working age population (16 years and older). Annual expected rates are expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=average and method=spline options. | 1976.1-1994.4 |
| UNEMPTOT | Natural log of total unemployment in given quarter. | Data used in creation of variable:
1) Quarterly unemployment rate data by state, 1976.1-1995.4, obtained from Local Area Unemployment Statistics, Bureau of Labor Statistics. 2) Quarterly employment rate data by state, 1976.1-1995.4, obtained from Current Employment Statistics, Bureau of Labor Statistics. |
Total unemployment data were not readily availble from the Bureau of Labor Statistics prior to 1976.1. Therefore, we calculated total unemployment from total employment and unemployment rate data that were readily available from the Bureau of Labor Statistics. | 1976.1-1994.4 |
| TUNEMPPC | Natural log of unemployment per capita ages 16-64 in given quarter. | Data used in creation of variable:
1) Quarterly unemployment rate data by state, 1976.1-1995.4, obtained from Local Area Unemployment Statistics, Bureau of Labor Statistics. 2) Quarterly employment rate data by state, 1976.1-1995.4, obtained from Current Employment Statistics, Bureau of Labor Statistics. 3) Annual state population data by age and sex obtained from the Bureau of the Census. |
Equal to natural logarithim of the ratio of unemployment per 1000 people ages 16-64. | 1976.1-1994.4 |
| TOTEMP | Natural log of total employment in given quarter. | Quarterly employment rate data by state, 1976.1-1995.4, obtained from Current Employment Statistics, Bureau of Labor Statistics. | No adjustments made before taking log of raw data. | 1976.1-1994.4 |
| Labor Market Variables |
| Variable | Description | Data | Construction | Dates |
| TOTEMPPC | Natural log of employment per capita ages 16-64 in given quarter. | Data used in creation of variable:
1) Quarterly employment rate data by state, 1976.1-1995.4, obtained from Current Employment Statistics, Bureau of Labor Statistics. 2) Annual state population data by age and sex obtained from the Bureau of the Census. |
Equal to natural logarithim of the ratio of total employment per 1000 people ages 16-64. | 1976.1-1994.4 |
| TRADE | Natural log of trade employment in given quarter. | Quarterly trade employment rate data by state, 1976.1-1995.4, obtained from Current Employment Statistics, Bureau of Labor Statistics. | No adjustments made before taking log of raw data. | 1976.1-1994.4 |
| TRADEPC | Natural log of trade employment per capita ages 16-64 in given quarter. | Data used in creation of variable:
1) Quarterly trade employment rate data by state, 1976.1-1995.4, obtained from Current Employment Statistics, Bureau of Labor Statistics. 2) Annual state population data by age and sex obtained from the Bureau of the Census. |
Equal to natural logarithim of the ratio of trade employment per 1000 people ages 16-64. | 1976.1-1994.4 |
| MANUFACT | Natural log of manufacturing employment in given quarter. | Quarterly manufacturing employment rate data by state, 1976.1-1995.4, obtained from Current Employment Statistics, Bureau of Labor Statistics. | No adjustments made before taking log of raw data. | 1976.1-1994.4 |
| MANFCTPC | Natural log of manufacturing employment per capita ages 16-64 in given quarter. | Data used in creation of variable:
1) Quarterly manufacturing employment rate data by state, 1976.1-1995.4, obtained from Current Employment Statistics, Bureau of Labor Statistics. 2) Annual state population data by age and sex obtained from the Bureau of the Census. |
Equal to natural logarithim of the ratio of manufacturing employment per 1000 people ages 16-64. | 1976.1-1994.4 |
| Labor Market Variables |
| Variable | Description | Data | Construction | Dates |
| RTLWAGE | Natural log of the real average weekly retail wage in given quarter (1990 dollars). | ES-202 annual state data series, 1978-1994, obtained from the Bureau of Labor Statistics. Contact: Mike Buso, (202) 606-6567. | Annual data are expanded to a quarterly series using SAS/ETS PROC EXPAND observed=average and method=spline options. Nominal dollar values deflated by regional CPI-Us (1990=100). | 1978.1-1994.4 |
| MANWAGE | Natural log of the real average weekly manufacturing wage (1990 dollars). | ES-202 annual state data series, 1978-1994, obtained from the Bureau of Labor Statistics. Contact: Mike Buso, (202) 606-6567. | Annual data are expanded to a quarterly series using SAS/ETS PROC EXPAND observed=average and method=spline options. Nominal dollar values deflated by regional CPI-Us (1990=100). | 1978.1-1994.4 |
| CPI90 | CPI-Us for four Census regions, 1990=100. | Data were downloaded from the Bureau of Labor Statistics web site. | Base changed from 1982-1984=100 to 1990=100. | 1978.1-1995.4 |
| FEM_EMPM | Natural log of the ratio of women between the ages of 15 and 44 to employed men in the state. | Data used in creation of variable:
1) Annual state level employment data by sex., 1978-1994, obtained from the Bureau of Labor Statistics. Contact: Roberto Morales (202) 606-6392. 2) Annual state population data by age and sex obtained from the Bureau of the Census. |
Unadjusted male employment data were adjusted by adjusted total employment data to obtain a consistent series as advised by Roberto Morales, BLS. Annual data for women between the ages of 15 and 44 and employed men expanded to quarterly series using SAS/ETS PROC EXPAND observed=average and method=spline options before taking ratio. | 1978.1-1994.4 |
| AFDC Program Variables |
| Variable | Description | Data | Construction | Dates |
| AFDC and Food Stamp Program Benefit Variables |
| MMB | Natural log of maximum monthly benefit including the value of Food Stamps payable to a three-person AFDC family during given quarter (1990 dollars). | Data used in creation of variable:
1) Typical maximum monthly AFDC benefit data compiled annually prior to 1982.3 and quarterly thereafter by the Administration for Children and Families (ACF). 2) Annual fiscal year Food Stamp maximum benefit and standard deduction data obtained from Food Stamp Program Information Division, Programs Reports and Analysis Branch. |
Equal to the nominal maximum monthly AFDC benefit for a three person family plus the nominal value of Food Stamps awarded when net income equals the maximum monthly AFDC benefit. Deflated to real dollars using the regional CPI-U (1990=100). | 1979.1 - 1994.4 |
| MAXPAY* | Natural log of typical maximum monthly AFDC benefit payable to a three-person family during given quarter (1990 dollars).(2) | Data are annual from 1979-1983 and quarterly thereafter. Data were obtained from the Administration for Children and Families (ACF). Contact: Evelyn Mills, (202) 401-4055. Semi-annual maximum monthly AFDC benefit data compiled from 1979 to 1994 also obtained from the Congressional Research Service (CRS). | Quarterly values were interpolated from annual data from 1979-1983 based on analysis of trends in typical maximum payments after 1983. ). The ACF data were checked against the CRS maximum monthly data. When a discrepancy appeared between the two series, an effort was made to explain the discrepancy and include the appropriate data. Deflated to real dollars using the regional CPI-U (1990=100). | 1979.1-1994.4 |
| NEED3* | Natural log of AFDC need standard for a three-person family during given quarter (1990 dollars). | Data are annual from 1979-1983 and quarterly thereafter. Data were obtained from the Administration for Children and Families (ACF). Contact: Evelyn Mills, (202) 401-4055. Semi-annual AFDC need standard data compiled from 1979 to 1994 also obtained from the Congressional Research Service (CRS). | Quarterly values were interpolated from annual data from 1979-1983 based on analysis of trends in typical maximum payments after 1983. ). The ACF data were checked against the CRS maximum monthly data. When a discrepancy appeared between the two series, an effort was made to explain the discrepancy and include the appropriate data. Deflated to real dollars using the regional CPI-U (1990=100). | 1979.1-1994.4 |
| AFDC Program Variables |
| Variable | Description | Data | Construction | Dates |
| PAYSTAND* | Natural log of AFDC payment standard for a three-person family during a given quarter (1990 dollars). | Data are annual (July) from 1979-1984 and semi-annual (January and July) from 1985-1994. Data were compiled by the Congressional Research Service and obtained either from various editions of Green Book and CRS reports. Contact: Carmen Solomon-Fears, (202) 707-7306. | Quarterly values were interpolated from annual and semi-annual data based on trends and changes in AFDC Typical Maximum Payment and Need Standard data. Deflated to real dollars using the regional CPI-U (1990=100). | 1979.1-1994.4 |
| EARNCUT* | Natural log of monthly earnings at which AFDC benefit amount falls to zero (1990 dollars). | Data used in creation of variable:
1) Quarterly AFDC payment standard data interpolated from annual and semi-annual data obtained from various editions of Green Book and CRS reports. 2) Formulas used by states to calculate AFDC benefits obtained from the Congressional Research Service. 3) Data on the Earned Income Tax Credit program. |
Calculated from the benefit formulas by setting benefits to zero and solving for countable income. Prior to 1981.4 and after 1984.3, EARNCUT is equal to countable income. In accordance with OBRA-81, however, EARNCUT from 1981.4 to 1984.3 is equal to countable income less the earned income tax credit at the calculated level of countable income. Deflated to real dollars using the regional CPI-U (1990=100). | 1979.1-1994.4 |
| CUTGIL | Continuous variable estimating effect of gross income limit at which family becomes ineligible for AFDC. | Data used in creation of variable:
1) EARNCUT, see derivation above. 2) AFDC need standard data were obtained from the Administration for Children and Families (ACF). |
CUTGIL is equal to the ratio of a state's AFDC earnings cutoff to the federal gross income limit. Prior to 1981.4, CUTGIL is equal to zero in all states because the gross income limit was, implicitly, infinity. | 1979.1-1994.4 |
| FOODADJ3* | Food Stamp benefit for a three-person family receiving the typical maximum AFDC benefit (1990 dollars). | Data used in creation of variable:
1) Maximum Food Stamp benefit data for a three-person family obtained from the USDA. 2) Food Stamp program standard deduction data obtained from the USDA. 3) Typical maximum AFDC payment for a three-person family obtained from the ACF. |
Equal to the maximum Food Stamp benefit for a three-person family less 30 percent of the difference of the typical maximum AFDC payment for a three-person family and the Food Stamp program standard deduction. Deflated to real dollars using the regional CPI-U (1990=100). | 1979.1-1995.3 |
| FOODSTP3* | Maximum Food Stamp benefit for a three-person family (1990 dollars). | Fiscal year data obtained from Program Reports and Analysis Branch, Program Information Division, Food, Nutrition, and Consumer Services, USDA. Contact: Arthur Foley, (703) 305-2490. | Value of benefit constant within quarter. Maximum benefits in both Alaska and Hawaii differ from the single maximum benefit designated for all 48 contiguous states. Deflated to real dollars using the regional CPI-U (1990=100). | 1979.1-1995.3 |
| AFDC Program Variables |
| Variable | Description | Data | Construction | Dates |
| FSDEDUCT* | Standard deduction taken from gross income used to determine the value of Food Stamp benefits (1990 dollars). | Fiscal year data obtained from Program Reports and Analysis Branch, Program Information Division, Food, Nutrition, and Consumer Services, USDA. Contact: Arthur Foley, (703) 305-2490. | Value of deduction constant within quarter. Standard deductions in both Alaska and Hawaii differ from the single standard deduction designated for all 48 contiguous states. Deflated to real dollars using the regional CPI-U (1990=100). | 1979.1-1995.3 |
| ATBRR | Average tax and benefit reduction rate between zero earnings and AFDC earnings cut-off. | Data used in creation of variable:
1) AFDC earnings cut-off (see above for derivation methodology). 2) Total disposable income at both AFDC earnings cut-off and zero earnings. 3) Maximum monthly benefit payable to a three-person AFDC family during given quarter, including the value of Food Stamps. 4) Data on EITC and FICA obtained from various editions of Green Book and Social Security Bulletin, Annual Statistical Supplement. 5) Formula provided by Gilbert Crouse, ASPE. |
ATBRR = 1 - (Y1 -Y0)/E1 , where ATBRR is the average tax and benefit reduction rate, Y1 is disposable income at the earnings cut-off, Y0 is disposable income at zero earnings, and E1 is the level of earnings at which AFDC benefits fall to zero. Disposable income equals: earnings + AFDC benefits + Food Stamp benefits + EITC - FICA. | 1979.1-1994 .4 |
| MTBRR | Marginal tax and benefit reduction rate at AFDC earnings cut-off. | Data used in creation of variable:
1) AFDC earnings cut-off (see above for derivation methodology). 2) Total disposable income at both AFDC earnings cut-off and $20 below AFDC earnings cut-off. 4) Data on EITC and FICA obtained from the various editions of Green Book and Social Security Bulletin, Annual Statistical Supplement. 5) Formula provided by Gilbert Crouse, ASPE. |
MTBRR = 1 - (Y1 -Y0)/(E1 - E0), where MTBRR is the marginal tax and benefit reduction rate $20 below the AFDC earnings cut-off, Y1 is disposable income at the earnings cut-off, Y0 is disposable income at $20 below the AFDC earnings cut-off, E1 is the level of earnings at which AFDC benefits fall to zero, and E0 is the level of earnings $20 below the AFDC earnings cut-off. Disposable income equals: earnings + AFDC benefits + Food Stamp benefits + EITC - FICA. | 1979.1-1994 .4 |
| AFDC Program Variables |
| Variable | Description | Data | Construction | Dates |
| AFDC Unemployed Parent Time-Limited Eligibility Variables |
| UP12M | Dummy variable for effects of AFDC-UP programs with no time- limited eligibility. | Data used in creation of variable:
1) AFDC-UP program initiation and termination dates obtained from ACF. Contact: Evelyn Mills, (202) 401-4055. 2) AFDC-UP program time eligibility policy data obtained from Characteristics of State Plans for Aid to Families with Dependent Children, 1990-1991 Edition. |
Equal to one in those quarters during which a state administers an AFDC-UP program with no time-limited eligibility. Otherwise, equal to zero.(3) | 1978.1-1994.4 |
| UP6M | Dummy variable for effects of AFDC-UP programs with time- limited eligibility. | Data used in creation of variable:
1) AFDC-UP program initiation and termination dates obtained from ACF. Contact: Evelyn Mills, (202) 401-4055. 2) AFDC-UP program time eligibility policy data obtained from Characteristics of State Plans for Aid to Families with Dependent Children, 1990-1991 Edition. |
Equal to one in those quarters during which a state administers an AFDC-UP program limiting eligibility to six months out of every twelve months. Otherwise, equal to zero.3,(4) | 1978.1-1994.4 |
| AFDC Federal Requirement Variables* |
| OBRA81 | Dummy variable for effects of AFDC provisions in OBRA-1981. | Information on OBRA-1981 obtained from Green Book and Overview of the AFDC Program, Fiscal Year 1994, published by ACF. | Equal to zero for all states prior to 1981.4 and equal to one for all states in 1981.4 and subsequent quarters. | 1978.1-1994.4 |
| DEFRA84 | Dummy variable for effects of AFDC provisions in DEFRA-1984. | Information on DEFRA-1984 obtained from Green Book and Overview of the AFDC Program, Fiscal Year 1994, published by ACF. | Equal to zero for all states prior to 1984.4 and equal to one for all states in 1984.4 and subsequent quarters. | 1978.1-1994.4 |
| OBRA87 | Dummy variable for effects of AFDC provisions in OBRA-1987. | Information on OBRA-1987 obtained from Green Book and Overview of the AFDC Program, Fiscal Year 1994, published by ACF. | Equal to zero for all states prior to 1988.2 and equal to one for all states in 1988.2 and subsequent quarters. | 1978.1-1994.4 |
| MEDCCXPN | Dummy variable for effects of Medicaid and Child Care expansion provisions in FSA-1988. | Information on FSA-1988 obtained from Green Book and Overview of the AFDC Program, Fiscal Year 1994, published by ACF. | Equal to zero for all states prior to 1990.2 and equal to one for all states in 1990.2 and subsequent quarters. | 1978.1-1994.4 |
| AFDC Program Variables |
| Variable | Description | Data | Construction | Dates |
| AFDC Federal Requirement Variables |
| JOBS | Dummy variable for effects of implementation of state JOBS programs. | State JOBS program implementation dates obtained from 1991 Green Book. | Equal to one in quarter during which a state implemented its JOBS program and all subsequent quarters. Equal to zero in all quarters prior to the quarter of implementation. | 1978.1-1994.4 |
| FSAUP1 | Dummy variable for the effects of federal mandate under FSA-1988 requiring states to implement AFDC-UP programs under. | Information obtained from ACF publication, Characteristics of State Plans for Aid to Families with Dependent Children, 1990-1991 Edition. | Equal to one from 1990.4 to 1994.4 for those states with no AFDC-UP program prior to the passage of FSA-1988 and required by FSA-1988 to establish an AFDC-UP program. Otherwise, equal to zero. | 1978.1-1994.4 |
| FSAUP2 | Dummy variable for the effects of the FSA-1988 provision mandating state AFDC-UP programs to require that at least one parent in a family participate in a work or educational program. | Information on FSA-1988 obtained from Green Book and Overview of the AFDC Program, Fiscal Year 1994, published by ACF. | Equal to zero for all states prior to 1993.4 and equal to one for all states in 1993.4 and subsequent quarters. | 1978.1-1994.4 |
| OBRA90 | Dummy variable for the exclusion of any children receiving foster care maintenance or adoption assistance payments from the AFDC assistance unit as mandated under OBRA-1990. | Information on OBRA-1990 obtained from Green Book and Overview of the AFDC Program, Fiscal Year 1994, published by ACF. | Equal to zero for all states prior to 1991.1 and equal to one for all states in 1991.1 and subsequent quarters. | 1978.1-1994.4 |
| OBRA93 | Dummy variable for AFDC provisions in OBRA-1993. | Information on OBRA-1993 obtained from Green Book and Overview of the AFDC Program, Fiscal Year 1994, published by ACF. | Equal to zero for all states prior to 1994.2 and equal to one for all states in 1994.2 and subsequent quarters. | 1978.1-1994.4 |
| Variable | Description | Data | Construction | Dates |
| AFDC Federal Waiver Variables |
| NOKIDS | Dummy variable for effects of waiver provisions that reduce or eliminate AFDC benefits for children born or conceived while the family is receiving AFDC. | Data on AFDC federal waivers obtained from the Administration for Children and Families. | Equal to one for New Jersey from 1992.4 forward; for Georgia from 1994.1 forward; and, for Wisconsin from 1994.3 forward. Otherwise, equal to zero. | 1978.1-1994.4 |
| WORKREQ | Dummy variable for effects of waiver provisions requiring AFDC recipients to engage in work, education or training activities outside of those under the state's JOBS program. | Data on AFDC federal waivers obtained from the Administration for Children and Families. | Equal to one for Utah from 1993.1 forward; for Oregon from 1993.1 forward; for Hawaii from 1994.1 forward; for Michigan from 1994.4 forward; and, for Connecticut from 1994.4 forward. Otherwise, equal to zero. | 1978.1-1994.4 |
| MEDEXPAN | Dummy variable for effects of waiver provisions that extend transitional Medicaid benefits for an additional one to two years. | Data on AFDC federal waivers obtained from the Administration for Children and Families. | Equal to one for Virginia from 1993.4 forward; for Vermont from 1994.2 forward; and, for Connecticut from 1994.4 forward. Otherwise, equal to zero. | 1978.1-1994.4 |
| AFDC Federal Waiver Variables |
| UP100 | Dummy variable for effects of waiver provisions that eliminate the 100-hour work limitation rule for AFDC-UP eligibility. | Data on AFDC federal waivers obtained from the Administration for Children and Families. | Equal to one for California from 1992.3 forward and for Connecticut from 1994.4 forward. Otherwise, equal to zero. | 1978.1-1994.4 |
| UP100WH | Dummy variable for effects of waiver provisions that eliminate both the 100-hour work limitation rule and work history requirement for AFDC-UP eligibility. | Data on AFDC federal waivers obtained from the Administration for Children and Families. | Equal to one Michigan from 1992.4 forward; for Iowa from 1993.4 forward; for Illinois from 1993.4 forward; for Vermont from 1994.2 forward; and, for Wisconsin from 1994.2 forward. Otherwise, equal to zero. | 1978.1-1994.4 |
| Other Program Variables |
| Variable | Description | Data | Construction | Dates |
| MEDGAIN | Continuous variable estimating effect of federally mandated expansion of Medicaid benefits under OBRA-89 and OBRA-90 to low-income mothers and children who are not AFDC eligible. | Existing annual variable through 1993 obtained from Aaron Yelowitz (1995). | Variable equal to zero before implementation of OBRA-89 and OBRA-90. Afterwards, variable equal to the percentage of children under the age of 18 in each state and year that are eligible for the Medicaid expansion. Values in 1994 equal value of variable in 1993 for each state. Annual series expanded to quarterly series using SAS/ETS PROC EXPAND with observed=average, method=join, and transformout=(ceil>=0) options. | 1978.1-1994.4 |
| MEDFAM3 | Log of the average monthly value (1990 dollars) of Medicaid benefit to a family of three in given quarter. | Annual state-level series obtained from Robert Moffitt (1978-1993) and supplemented with 1994 Medicaid 2082 data obtained from Health Care Financing Administration. | Annual benefit value for a family of three equal to two times the average benefit value to an AFDC child plus the average benefit value to an AFDC adult in a given state. An average monthly benefit for a given year was then obtained by dividing the annual benefit value by 12. This annual series was then expanded to a quarterly series using SAS/ETS PROC EXPAND with observed=average and method=join. MEDFAM3 is deflated to real dollars using the regional CPI-U (1990=100). | 1978.1-1994.4 |
| GACHNG | Continuos variable measuring the size of state general assistance caseload changes to major state level policy initiatives. | State general assistance caseload data obtained from the Administration for Children and Families (ACF) including ACF publications, Quarterly Public Assistance Statistics (1981-1993) and Public Assistance Statistics (1978-1980). GACHNG variable derived from GACUT variable previously constructed by The Lewin Group. | GACHNG variable set to zero in the first quarter of the sample period. When a general assistance (GA) cut or increase occurs in a state, the size of cut per capita is the difference between the average monthly GA caseload in the three months following the quarter in which the cut occurred and in the three months preceding that quarter divided by the state's population. GACHNG variable set equal to the resulting number from the quarter of the change through the quarter in which the next change occurs. Additional changes are added to previous change(s). | 1978.1-1994.4 |
| SSIBEN | Log of the maximum SSI payment, federal plus state supplement in given quarter (1990 dollars). | Data on SSI federal and state supplement benefits obtained from various editions of the Social Security Administration publication, State Assistance Programs for SSI Recipients. | Benefit rates became effective on July 1 from 1979 through 1983. From 1984 through 1995, benefit rates became effective January 1. | 1978.1-1995.4 |
| Other Program Variables |
| Variable | Description | Data | Construction | Dates |
| SSIKIDS | Log of average monthly number of SSI child recipients in given quarter. | Data on SSI child recipients for December 1977-1994 obtained from various editions of the Social Security Bulletin, Annual Statistical Supplement. | Average monthly number of child recipients for each month derived from December data using SAS/ETS PROC EXPAND with from=month12.12, to=month, observed=average, method=join, and transforumout=(floor>=0). Monthly series then expanded to quarterly series using SAS/ETS PROC EXPAND with observed=average and method=join options. | 1978.1-1994.4 |
| ZEBLEY | Log of average monthly number of SSI child recipients in given quarter eligible for SSI as a result of Sullivan v. Zebley. | Data on Zebley SSI child recipients for June and December (1991-1995) obtained from Charles Scott, Social Security Administration. | Average monthly number of Zebley SSI child recipients for year derived from June and December data using SAS/ETS PROC EXPAND with from=month6.3, to=month, observed=average, method=join, and transforumout=(floor>=0). Annual series then expanded to quarterly series using SAS/ETS PROC EXPAND with observed=average and method=join options. | 1978.1-1995.4 |
| SSARD80 | Change in SSDI initial allowance rate between 1977 and 1978 | Parsons (1991) | Variable equals the change in SSDI initial allowance rate in a given state between 1977 and 1978. The variable is interacted with the calendar year dummy for 1980 in the Basic model. | 1978.1-1994.4 |
| UINSUR | Log of the quotient of the insured unemployment rate divided by the unemployment rate. | Quarterly total and insured unemployment rate data by state from the Bureau of Labor Statistics via BLS web site. | Variable calculated by dividing insured unemployment rate by total unemployment rate and taking log of the resulting quotient. | 1978.1-1995.4 |
| Child Support Enforcement Laws |
| DIMMWITH | Dummy variable representing existence of immediate withholding statutes in given quarter. | See Gaylin, Daniel S. and McLanahan, Sara S. (1995). Data provided by Daniel S. Gaylin. | Specification assumes statute goes into effect on January 1 of given year. Equal to one if state has statute in effect in given quarter. Otherwise, equal to zero. | 1978.1-1994.4 |
| DMANWITH | Dummy variable representing existence of mandatory withholding statutes in given quarter. | See Gaylin, Daniel S. and McLanahan, Sara S. (1995). Data provided by Daniel S. Gaylin. | Specification assumes statute goes into effect on January 1 of given year. Equal to one if state has statute in effect in given quarter. Otherwise, equal to zero. | 1978.1-1994.4 |
| Other Program Variables |
| Variable | Description | Data | Construction | Dates |
| Child Support Enforcement Laws |
| DPATLARM | Dummy variable representing existence of paternal long-arm statutes in given quarter. | See Gaylin, Daniel S. and McLanahan, Sara S. (1995). Data provided by Daniel S. Gaylin. | Specification assumes statute goes into effect on January 1 of given year. Equal to one if state has statute in effect in given quarter. Otherwise, equal to zero. | 1978.1-1994.4 |
| DPRESUMP | Dummy variable representing existence of presumptive guideline statutes in given quarter. | See Gaylin, Daniel S. and McLanahan, Sara S. (1995). Data provided by Daniel S. Gaylin. | Specification assumes statute goes into effect on January 1 of given year. Equal to one if state has statute in effect in given quarter. Otherwise, equal to zero. | 1978.1-1994.4 |
| Abortion Restrictions |
| ABRTCAID | Dummy variable representing the existence of laws limiting Medicaid funding for abortions. | Merz, Jon F. , et al. A Review of Abortion Policy: Legality, Medicaid Funding, and Parental Involvement, 1967-1994. (Working Paper No.: DRU-1096-NICHD.) Rand, May 1995. | Equal to one if state enforces law limiting Medicaid funding for abortions in given quarter. Otherwise, equal to zero. | 1978.1-1994.4 |
| ABRTMINR | Dummy variable representing the existence of laws requiring parental consent and/or notification before a minor may obtain an abortion. | Merz, Jon F. , et al. A Review of Abortion Policy: Legality, Medicaid Funding, and Parental Involvement, 1967-1994. (Working Paper No.: DRU-1096-NICHD.) Rand, May 1995. | Equal to one if state enforces parental consent and/or notification limiting laws regulating minors access to abortion services in given quarter. Otherwise, equal to zero. | 1978.1-1994.4 |
1. 0 Variables followed by "*" are transitional variables used to construct other variables and not used in the models.
2. 0 A given family's maximum AFDC benefit may differ from the state's "typical" benefit as calculated by the ACF due to factors such as: locality, housing arrangements, family composition, or special needs.
3. 0 For Colorado, which has administered an AFDC-UP program limiting eligibility to nine months out of every twelve month period since 1990.4, UP12M and UP6M are both set equal to 0.5.
4. 0 Time-limited eligibility is a program option available only to those states that initiated an AFDC-UP program after the passage of FSA-88.
